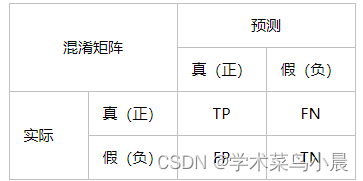
CNN,卷积神经网络,Convolution Neural Network
卷积计算公式:
N = (W-F+2p)/s+1
1 经典网络
按照时间顺序
1.1 LeNet
LeNet是 Yann LeCun在1998年提出,用于解决手写数字识别的视觉任务。自那时起,CNN的最基本的架构就定下来了:卷积层、池化层、全连接层。
1.2 AlexNet
AlexNet是2012年ImageNet竞赛冠军获得者Hinton和他的学生Alex Krizhevsky设计的,把CNN的基本原理应用到了很深很宽的网络中。
主要参数:AlexNet网络包含8层,其中前5层为卷积-池化层,后3层为全连接层;输入224×224×3的图像,第一卷积层用96个11×11×3的卷积核对进行滤波,步幅4像素;全连接的每层有4096个神经元,最后一个完全连接的层的输出被馈送到1000路SoftMax,它产生超过1000个类别标签的分布;整个网络共650000个神经元。
特点:
- 使用ReLU作为激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题
- 使用Dropout(丢弃学习)随机忽略一部分神经元防止过拟合
- 在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果
- 提出了LRN(Local Response Normalization,局部正规化)层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力
- 使用CUDA加速深度卷积网络的训练,利用GPU强大的并行计算能力,处理神经网络训练时大量的矩阵运算
1.3 VGG
- 网络深度:16-19层
- 5组卷积-池化,3个全连接
- 三个全连接层,前两层都有4096通道,第三层共1000路及代表1000个标签类别;最后一层为softmax层
- 所有卷积层有相同的配置,即卷积核大小为3x3,步长为1,填充为1
1.4 GoogleNet
2 网络结构
2.1 卷积层
通过卷积操作,进行特征提取和降维。
2.2 激活层
将前一层的输出,通过非线性的激活函数进行处理,用以模拟任意维度的函数,增强网络的表征能力。
常用的激活函数:
- 阶跃函数(用的较少)
- sigmoid函数:
- 优点:平滑,易求导
- 缺点:激活函数计算量大,反向传播求误差梯度时,求导涉及除法;反向传播时,很容易就会出现梯度消失的情况,从而无法完成深层网络的训练
- 改善方案:归一化,用sk-learn函数处理
- tanh函数 常用于NLP,其他类似sigmiod函数
- Relu函数(常用),优点:
- 更加有效率的梯度下降以及反向传播,避免了梯度爆炸和梯度消失问题
- 计算过程简单
- softmax函数,特点:多分类模型适用
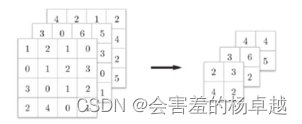
2.3 池化
也称子采样层或下采样层(Subsampling Layer),目的是缩小高、长方向上的空间的运算,以降低计算量,提高泛化能力。
计算方式:
- Max池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域取最大值,形成的新矩阵。在图像识别领域,主要使用Max池化
- Average池化:对于每个输入矩阵,我们将其切割成若干大小相等的正方形小块,对各个参与池化计算的区域计算平均值
池化层特征:
- 没有要学习的参数。池化层和卷积层不同,没有要学习的参数。池化只是从目标区域中取最大值(或者平均值),所以不存在要学习的参数
- 通道数不发生变化。经过池化运算,输入数据和输出数据的通道数不会发生变化
- 对微小的位置变化具有鲁棒性(健壮)。输入数据发生微小偏差时,池化仍会返回相同的结果
2.4全连接层
这个网络层相当于多层感知机(Multi-Layer Perceptron,简称MLP),其在整个卷积神经网络中起到分类器的作用。
通过前面多个“卷积-激活-池化”层的反复处理,待处理的数据特性已有了显著提高:一方面,输入数据的维度已下降到可用传统的前馈全连接网络来处理了;另一方面,此时的全连接层输入的数据已不是“泥沙俱下、鱼龙混杂”,而是经过反复提纯过的结果,因此输出的分类品质要高得多。