凸优化基础学习——凸集
文章内容全部来自对Stephen Boyd and Lieven vandenberghe的Convex Optimization的总结归纳。
电子书资源:
链接:https://pan.baidu.com/s/1dP5zI6h3BEyGRzSaJHSodg?pwd=0000
提取码:0000
基本概念
仿射集合
**仿射集合:**通过集合 C ⊆ R n C\subseteq \mathbf{R}^n C⊆Rn中任意两个不同点的直线仍然在集合 C C C中,则称集合 C C C是仿射的。
另一种等价定义:对于任意 x 1 , x 2 ∈ C x_1,x_2\in C x1,x2∈C及 θ ∈ R \theta\in\mathbf{R} θ∈R有 θ x 1 + ( 1 − θ ) x 2 ∈ C \theta x_1+\left( 1-\theta \right) x_2\in C θx1+(1−θ)x2∈C,即 C C C中包含了 C C C中任意两点的系数之和为1的线性组合。
**仿射组合:**仿射集合的概念可以扩展到多个点的情况,如果 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1,那么具有 θ 1 x 1 + ⋯ + θ k x 1 = 1 \theta_1x_1+\cdots+\theta_kx_1=1 θ1x1+⋯+θkx1=1形式的点为 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的仿射组合。
**仿射包:**集合 C ⊆ R n C\subseteq\mathbf{R}^n C⊆Rn中的点的所有仿射组合组成的集合为 C C C的仿射包,记作 a f f C : \mathbf{aff}C: affC:
**仿射维数:**定义集合
C
C
C的仿射维数为其仿射包的维数。
a
f
f
C
=
{
θ
1
x
1
+
⋯
+
θ
k
x
k
∣
x
1
,
⋯
,
x
k
∈
C
,
θ
1
+
⋯
+
θ
k
=
1
}
\mathbf{aff}C=\{\theta_1x_1+\cdots+\theta_kx_k|x_1,\cdots,x_k\in C,\theta_1+\cdots+\theta_k=1\}
affC={θ1x1+⋯+θkxk∣x1,⋯,xk∈C,θ1+⋯+θk=1}
性质:
- 仿射集合 C C C可以表示成
C = V + x 0 = v + x 0 ∣ v ∈ V C=V+x_0={v+x_0|v\in V} C=V+x0=v+x0∣v∈V
其中 C C C是一个子空间,并且关于加法和数乘是封闭的。 x 0 x_0 x0是 C C C中任意一点。**仿射集合 C C C**的维数定义为子空间 V = C − x 0 V=C-x_0 V=C−x0的维度。
- 一个仿射集合包含其中任意点的仿射组合,即如果 C C C是一个仿射集合, x 1 , ⋯ , x k ∈ C x_1,\cdots,x_k\in C x1,⋯,xk∈C,并且 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1,那么 θ 1 x 1 + ⋯ + θ k x k \theta_1x_1+\cdots+\theta_kx_k θ1x1+⋯+θkxk仍然在 C C C中。
- 仿射包是包含 C C C的最小仿射集合。
常见例子
- 线性方程组 C = { x ∣ A x = b } C=\{x|Ax=b\} C={x∣Ax=b}的解集是一个仿射集合,其子空间就是 A A A的零空间。同时任意仿射集合可以表示成一个线性方程组的解集。
凸集
**凸集:**如果
C
C
C中任意两点间的线段仍然在
C
C
C中,及对于任意
x
1
,
x
2
∈
C
x_1,x_2\in C
x1,x2∈C和满足
0
≤
θ
≤
1
0\le\theta\le1
0≤θ≤1的
θ
\theta
θ都有
θ
x
1
+
(
1
−
θ
)
x
2
∈
C
\theta x_1+(1 - \theta)x_2\in C
θx1+(1−θ)x2∈C
或者说如果集合中的每一个点都可以被其他的点沿着它们之间的一条无阻碍(整条路径都在集合中)的路径看见,那么这个集合就被称为凸集。
**凸组合:**称 θ 1 x 1 + ⋯ + θ k x 1 \theta_1x_1+\cdots+\theta_kx_1 θ1x1+⋯+θkx1为点 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的一个凸组合,其中 θ 1 + ⋯ + θ k = 1 \theta_1+\cdots+\theta_k=1 θ1+⋯+θk=1并且 θ i ≥ 0 , i = 1 , ⋯ , k 。 \theta_i\ge0,i=1,\cdots,k。 θi≥0,i=1,⋯,k。
**凸包:**集合
C
C
C中所有点构成的凸组合的集合为其凸包,记为
conv
C
:
\text{\textbf{conv}}C:
convC:
conv
C
=
{
θ
1
x
1
+
⋯
+
θ
k
x
k
∣
x
i
∈
C
,
θ
i
≥
0
,
i
=
1
,
⋯
,
k
,
θ
1
+
⋯
+
θ
k
=
1
}
\text{\textbf{conv}}C=\{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i\ge0,i=1,\cdots,k,\theta_1+\cdots+\theta_k=1\}
convC={θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k,θ1+⋯+θk=1}
性质:
- 仿射集是凸集。
- 一个集合的凸集等价于集合中包含了其中所有点的凸组合,可以理解为混合和加权平均。
- 凸包是包含集合 C C C的最小凸集,即有如果 B B B是包含 C C C的凸集,那么 conv C ⊆ B \text{\textbf{conv}}C\subseteq B convC⊆B。
锥
**锥:**如果对于任意 x ∈ C x\in C x∈C和 θ ≥ 0 \theta \ge0 θ≥0都有 θ x ∈ C \theta x\in C θx∈C,那么我们就称集合 C C C是锥或者说是非负齐次的。
**凸锥:**对于任意
x
1
,
x
2
∈
C
x_1,x_2\in C
x1,x2∈C和
θ
1
,
θ
2
≥
0
,
都有
\theta_1,\theta_2\ge0,都有
θ1,θ2≥0,都有
θ
1
x
1
+
θ
2
x
2
∈
C
\theta_1x_1+\theta_2x_2\in C
θ1x1+θ2x2∈C
具有这类形式的点构成了二维的扇形
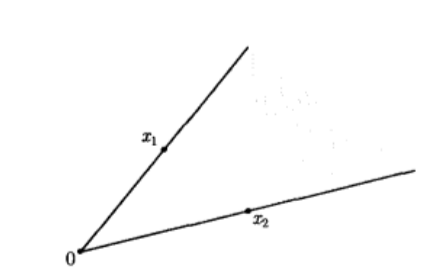
**锥组合(非负线性组合):**具有 θ 1 x 1 + ⋯ + θ k x 1 , θ 1 , ⋯ , θ k ≥ 0 \theta_1x_1+\cdots+\theta_kx_1,\theta_1,\cdots,\theta_k\ge0 θ1x1+⋯+θkx1,θ1,⋯,θk≥0形式的点称为 x 1 , ⋯ , x k x_1,\cdots,x_k x1,⋯,xk的锥组合。
**锥包:**集合
C
C
C中元素的所有锥组合的集合,即
{
θ
1
x
1
+
⋯
+
θ
k
x
k
∣
x
i
∈
C
,
θ
i
≥
0
,
i
=
1
,
⋯
,
k
}
\{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i\ge0,i=1,\cdots,k\}
{θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k}
性质
-
如果 x i x_i xi均属于凸锥 C C C,那么 x i x_i xi的每一个锥组合也在 C C C中。即集合 C C C是凸锥的充分必要条件是它包含其元素的所有锥组合。
-
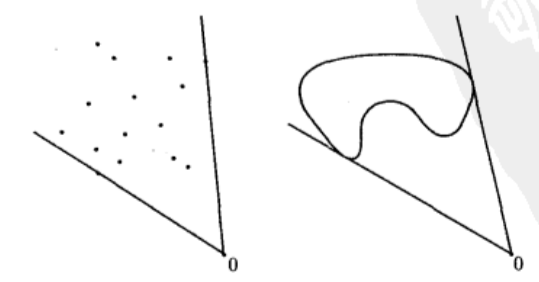
锥包是包含 C C C的最小的凸锥。左图代表由点组成的一个集合 C C C的凸锥,右图代表由一块连续的区域组成的集合 C C C的凸锥。
常见例子
简单例子
-
任意直线都是仿射的。如果直线通过零点,则是子空间,因此,也是凸锥。
-
一个线段是凸的,但不是仿射的(除非退化为一个点)。
-
空集、任意一个点、全空间 R n \mathbf{R}^n Rn都是 R n \mathbf{R}^n Rn的仿射(自然也是凸的)子集。
-
一条射线,既具有形式 { x 0 + θ v ∣ θ ≥ 0 } , v ≠ 0 \{x_0+\theta v|\theta\ge0\},v\neq0 {x0+θv∣θ≥0},v=0的集合,是凸的但不是仿射的。如果射线的基点 x 0 x_0 x0是0,则它是凸锥。
-
任意子空间是仿射的、凸锥。
超平面和半空间
**超平面:**具有以下形式的集合称为超平面
{
x
∣
a
T
x
=
b
}
\{x|a^Tx=b\}
{x∣aTx=b}
其中
a
∈
R
n
,
a
≠
0
a\in \mathbf{R}^n,a\neq0
a∈Rn,a=0并且
b
∈
R
b\in\mathbf{R}
b∈R。显然超平面为关于
x
x
x的非平凡线性方程的解空间,因此其是一个仿射集合(当然也是凸集了)。
在几何上,超平面可以看作是和给定向量 a a a的内积为常数的点的集合;也可以看作是法线方向为 a a a的超平面,而常数 b ∈ R b\in\mathbf{R} b∈R决定了这个平面的偏移量。如下图所示

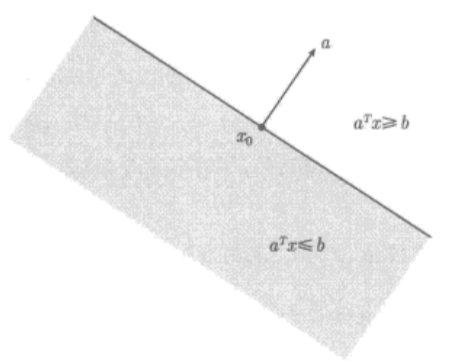
**半空间:**具有以下形式的集合称为半空间,其中
a
≠
0
a\neq0
a=0,半空间是凸的,但不是仿射的。
{
x
∣
a
T
x
≤
b
}
\{x|a^Tx\le b\}
{x∣aTx≤b}
**开半空间:**开半空间是半空间的内部,即具有以下形式的集合
{
x
∣
a
T
x
<
b
}
\{x|a^Tx< b\}
{x∣aTx<b}
Euclid球和椭球
Euclid球:
R
n
\mathbf{R}^n
Rn中的Euclid球具有下面的形式,利用范数的三角不等式和齐次性可以证明它是凸集。
B
(
x
c
,
r
)
=
{
x
∣
∥
x
−
x
c
∥
2
⩽
r
}
=
{
x
∣
(
x
−
x
c
)
T
(
x
−
x
c
)
⩽
r
2
}
B\left(x_c, r\right)=\left\{x \mid\left\|x-x_c\right\|_2 \leqslant r\right\}=\left\{x \mid\left(x-x_c\right)^T\left(x-x_c\right) \leqslant r^2\right\}
B(xc,r)={x∣∥x−xc∥2⩽r}={x∣(x−xc)T(x−xc)⩽r2}
其中
r
>
0
r>0
r>0,
∥
∥
2
\left\|\right\|_2
∥∥2表示Euclid范数,
x
c
x_c
xc表示球心,标量
r
r
r为半径。
B
(
x
c
,
r
)
B\left(x_c, r\right)
B(xc,r)为距离圆心
x
c
x_c
xc距离不超过
r
r
r的所有点组成。
Euclid球的另外一种表达式如下
B
(
x
c
,
r
)
=
{
x
c
+
r
u
∣
∥
u
∥
2
⩽
1
}
B\left(x_c, r\right)=\left\{x_c+r u \mid\|u\|_2 \leqslant 1\right\}
B(xc,r)={xc+ru∣∥u∥2⩽1}
**椭球:**具有以下形式的集合称为椭球,其同样为凸集
E
=
{
x
∣
(
x
−
x
c
)
T
P
−
1
(
x
−
x
c
)
⩽
1
}
\mathcal{E}=\left\{x \mid\left(x-x_c\right)^T P^{-1}\left(x-x_c\right) \leqslant 1\right\}
E={x∣(x−xc)TP−1(x−xc)⩽1}
其中,
P
=
P
T
≻
0
P=P^T\succ0
P=PT≻0,即
P
P
P为对称的正定矩阵。
x
c
x_c
xc为椭圆中心,矩阵
P
P
P决定了椭球从
x
c
x_c
xc向各个方向扩展的幅度。
E
\mathcal{E}
E的半轴长度由
λ
i
\sqrt{\lambda_i}
λi决定,其中
λ
i
\lambda_i
λi为
P
P
P的特征值。
椭球的另外一个表示形式为
E
=
{
x
c
+
A
u
∣
∥
u
∥
2
⩽
1
}
\mathcal{E}=\left\{x_c+A u \mid\|u\|_2 \leqslant 1\right\}
E={xc+Au∣∥u∥2⩽1}
范数球和范数锥
**范数球:**定义如下,由范数的一般性质可以知道其为凸的
C
=
{
(
x
,
t
)
∣
∥
x
∥
⩽
t
}
⊆
R
n
+
1
C=\{(x, t) \mid\|x\| \leqslant t\} \subseteq \mathbf{R}^{n+1}
C={(x,t)∣∥x∥⩽t}⊆Rn+1
**范数锥:**关于范数
∥
∥
\left\|\right\|
∥∥的范数锥是集合,其为一个凸锥
C
=
{
(
x
,
t
)
∣
∥
x
∥
⩽
t
}
⊆
R
n
+
1
C=\{(x, t) \mid\|x\| \leqslant t\} \subseteq \mathbf{R}^{n+1}
C={(x,t)∣∥x∥⩽t}⊆Rn+1
**二阶锥:**由Euclid范数定义的范数锥称为范数锥,也可以称为二次锥、Lorentz锥或者冰淇淋锥。
C
=
{
(
x
,
t
)
∈
R
n
+
1
∣
∥
x
∥
2
⩽
t
}
=
{
[
x
t
]
∣
[
x
t
]
T
[
I
0
0
−
1
]
[
x
t
]
⩽
0
,
t
⩾
0
}
\begin{aligned} C & =\left\{(x, t) \in \mathbf{R}^{n+1} \mid\|x\|_2 \leqslant t\right\} \\ & =\left\{\left[\begin{array}{l} x \\ t \end{array}\right] \mid\left[\begin{array}{l} x \\ t \end{array}\right]^T\left[\begin{array}{cc} I & 0 \\ 0 & -1 \end{array}\right]\left[\begin{array}{l} x \\ t \end{array}\right] \leqslant 0, t \geqslant 0\right\} \end{aligned}
C={(x,t)∈Rn+1∣∥x∥2⩽t}={[xt]∣[xt]T[I00−1][xt]⩽0,t⩾0}
下图是一个
R
3
\mathbf{R}^3
R3的二阶锥

多面体
**多面体:**定义为有限个线性等式和不等式的解集:
P
=
{
x
∣
a
j
T
x
⩽
b
j
,
j
=
1
,
⋯
,
m
,
c
j
T
x
=
d
j
,
j
=
1
,
⋯
,
p
}
\mathcal{P}=\left\{x \mid a_j^T x \leqslant b_j, j=1, \cdots, m, c_j^T x=d_j, j=1, \cdots, p\right\}
P={x∣ajTx⩽bj,j=1,⋯,m,cjTx=dj,j=1,⋯,p}
其为有限个半空间和超平面的交集,下图为五个半空间组成的一个多面体示意图。
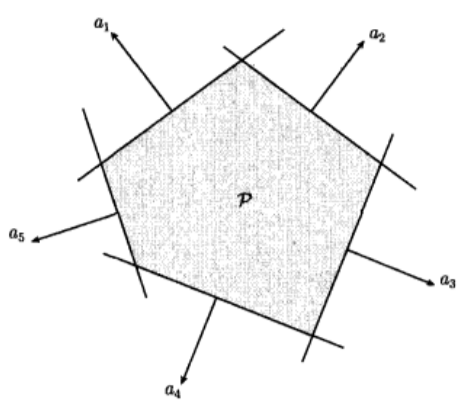
多面体也可以写成如下更为紧凑的形式:
P
=
{
x
∣
A
x
⪯
b
,
C
x
=
d
}
A
=
[
a
1
T
⋮
a
m
T
]
,
C
=
[
c
1
T
⋮
c
p
T
]
,
\begin{gathered} \mathcal{P}=\{x \mid A x \preceq b, C x=d\} \\ A=\left[\begin{array}{c} a_1^T \\ \vdots \\ a_m^T \end{array}\right], \quad C=\left[\begin{array}{c} c_1^T \\ \vdots \\ c_p^T \end{array}\right], \end{gathered}
P={x∣Ax⪯b,Cx=d}A=
a1T⋮amT
,C=
c1T⋮cpT
,
其中
⪯
\preceq
⪯表示
R
m
\mathbf{R}^m
Rm上的向量不等式或分量不等式。
半正定锥
**半正定锥:**利用
S
n
\mathbf{S}^n
Sn表示对称
n
×
n
n\times n
n×n矩阵的集合,
S
+
n
\mathbf{S}^n_+
S+n表示对称半正定矩阵的集合,
S
+
+
n
\mathbf{S}^n_{++}
S++n表示对称正定矩阵的集合,即
S
n
=
{
X
∈
R
n
×
n
∣
X
=
X
T
}
S
+
n
=
{
X
∈
S
n
∣
X
⪰
0
}
S
+
+
n
=
{
X
∈
S
n
∣
X
≻
0
}
\begin{aligned} & \mathbf{S}^n=\left\{X \in \mathbf{R}^{n \times n} \mid X=X^T\right\} \\ & \mathbf{S}_{+}^n=\left\{X \in \mathbf{S}^n \mid X \succeq 0\right\} \\ & \mathbf{S}_{++}^n=\left\{X \in \mathbf{S}^n \mid X \succ 0\right\} \end{aligned}
Sn={X∈Rn×n∣X=XT}S+n={X∈Sn∣X⪰0}S++n={X∈Sn∣X≻0}
其中集合
S
+
n
\mathbf{S}^n_+
S+n为一个凸锥。
保凸运算
保凸运算可以从已知的凸集构造出其他凸集,能够用来确定和构建具有凸性的集合。
交集
凸集的交集运算是保凸的:如果 S 1 S_1 S1和 S 2 S_2 S2是凸集,那么 S 1 ∩ S 2 S_1\cap S_2 S1∩S2也是凸集,这个性质也能够扩展到无穷多个集合的交。
仿射函数
**仿射函数:**如果一个函数是一个线性函数和一个常数的和,即具有 f ( x ) = A x + b f(x)=Ax+b f(x)=Ax+b的形式,其中 A ∈ R m × n , b ⊆ R m A\in\mathbf{R^{m\times n}},b\subseteq\mathbf{R^m} A∈Rm×n,b⊆Rm。
如果
S
⊆
R
n
S\subseteq\mathbf{R}^n
S⊆Rn是凸的,并且
f
:
R
n
→
R
m
f:\mathbf{R^n}\rightarrow\mathbf{R^m}
f:Rn→Rm是仿射函数。那么,
S
S
S在
f
f
f下的象
f
(
S
)
=
{
f
(
x
)
∣
x
∈
S
}
f(S)=\{f(x)\mid x\in S\}
f(S)={f(x)∣x∈S}
也是凸的。同样类似的,如果
f
:
R
k
→
R
n
f:\mathbf{R^k}\rightarrow\mathbf{R^n}
f:Rk→Rn是仿射函数,那么
S
S
S在
f
f
f下的原象
f
−
1
(
S
)
=
{
x
∣
f
(
x
)
∈
S
}
f^{-1}(S)=\{x\mid f(x)\in S\}
f−1(S)={x∣f(x)∈S}
也是凸的。
例子
- 伸缩与平移:如果 S ⊆ R n S\subseteq\mathbf{R}^n S⊆Rn, α ∈ R \alpha\in\mathbf{R} α∈R并且 a ∈ R n a\in\mathbf{R^n} a∈Rn,那么,集合 α S \alpha S αS和集合 S + a S + a S+a是凸的。
- 直积:如果 S 1 S_1 S1和 S 2 S_2 S2都是凸集,那么其直积也是凸集,其直积可以表示为
S 1 × S 2 = { ( x 1 , x 2 ) ∣ x 1 ∈ S 1 , x 2 ∈ S 2 } S_{1} \times S_{2}=\left\{\left(x_{1}, x_{2}\right) \mid x_{1} \in S_{1}, x_{2} \in S_{2}\right\} S1×S2={(x1,x2)∣x1∈S1,x2∈S2}
线性分式和透视函数
**透视函数:**定义 P : R n + 1 → R n P:\mathbf{R^{n+1}\rightarrow\mathbf{R^n}} P:Rn+1→Rn, P ( z , t ) = z / t P(z,t)=z/t P(z,t)=z/t为透视函数,其定义域为 dom P = R n × R + + \textbf{dom}P=\mathbf{R^n}\times\mathbf{R_{++}} domP=Rn×R++。其中 R + + \mathbf{R_{++}} R++表示正实数集合。透视函数对向量进行伸缩,或者称为规范化,使得最后一维分量为1并且舍弃掉。
**性质:**如果
C
⊆
dom
P
C\subseteq\textbf{dom}P
C⊆domP是凸集,那么他的象
P
(
C
)
=
{
P
(
x
)
∣
x
∈
C
}
P(C)=\{P(x)\mid x \in C \}
P(C)={P(x)∣x∈C}
也是凸集。同样一个凸集在透视函数的原象也是凸的。
**线性分式函数:**线性分式函数由透视函数和仿射函数符合而成。设
g
:
R
n
→
R
m
+
1
g:\mathbf{R^n}\rightarrow\mathbf{R^{m+1}}
g:Rn→Rm+1是仿射的,即
g
(
x
)
=
[
A
c
T
]
x
+
[
b
d
]
g(x)=\left[\begin{array}{c} A \\ c^{T} \end{array}\right] x+\left[\begin{array}{l} b \\ d \end{array}\right] \\
g(x)=[AcT]x+[bd]
其中
A
∈
R
m
×
n
,
b
∈
R
m
,
c
∈
R
n
A\in\mathbf{R^{m\times n}},b\in\mathbf{R^m},c\in\mathbf{R^n}
A∈Rm×n,b∈Rm,c∈Rn并且
d
∈
R
d\in\mathbf{R}
d∈R。则由$f=P \circ g
给出的函数
给出的函数
给出的函数f:\mathbf{Rn}\rightarrow\mathbf{Rm}$
f
(
x
)
=
(
A
x
+
b
)
/
(
c
T
x
+
d
)
,
dom
f
=
{
x
∣
c
T
x
+
d
>
0
}
\quad f(x)=(A x+b) /\left(c^{T} x+d\right), \quad \operatorname{dom} f=\left\{x \mid c^{T} x+d>0\right\}
f(x)=(Ax+b)/(cTx+d),domf={x∣cTx+d>0}
称为线性分式(或者投射)函数。值得注意的是如果
c
=
0
,
d
>
0
c=0,d>0
c=0,d>0,则
f
f
f的定义域为
R
n
\mathbf{R}^n
Rn,并且
f
f
f是仿射函数。因此,我饿们可以将仿射和线性函数视为特殊的线性分式函数。
**性质:**类似于透视函数,线性分式函数也是保凸的。如果 C C C是凸集,那么其在线性分式函数下的象和原象都是凸的。
广义不等式
正常锥和广义不等式
**正常锥:**满足以下条件的锥 K ⊆ R n K\subseteq \mathbf{R}^n K⊆Rn为正常锥
- K K K是凸的
- K K K是闭的
- K K K是实的,即具有非空内部
- K K K是尖的,即不包含直线(或者等价地, x ∈ K , − x ∈ K ⇒ x = 0 x\in K,-x\in K\Rightarrow x=0 x∈K,−x∈K⇒x=0)
正常锥常用来定义广义不等式。用正常锥
K
K
K可以定义
R
n
\mathbf{R^n}
Rn上的偏序关系如下
x
⪯
K
y
⟺
y
−
x
∈
K
x\preceq_Ky\Longleftrightarrow y-x\in K
x⪯Ky⟺y−x∈K
同样,可以定义相应的严格偏序关系
x
≺
K
y
⟺
y
−
x
∈
int
K
x\prec_Ky\Longleftrightarrow y-x\in \textbf{int}K
x≺Ky⟺y−x∈intK
广义不等式
⪯
\preceq
⪯的性质
- ⪯ K \preceq_K ⪯K对于加法是保序的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 u ⪯ K v u\preceq_Kv u⪯Kv,那么 x + u ⪯ K y + v x+u\preceq_Ky+v x+u⪯Ky+v。
- ⪯ K \preceq_K ⪯K具有传递性:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 y ⪯ K z y\preceq_Kz y⪯Kz,那么 x ⪯ K z x\preceq_Kz x⪯Kz。
- ⪯ K \preceq_K ⪯K对于非负数乘是保序的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 α ≥ 0 \alpha\ge 0 α≥0,那么 α x ⪯ K α y \alpha x\preceq_K\alpha y αx⪯Kαy。
- ⪯ K \preceq_K ⪯K是自反的: x ⪯ K x x\preceq_Kx x⪯Kx。
- ⪯ K \preceq_K ⪯K是反对称的:如果 x ⪯ K y x\preceq_Ky x⪯Ky并且 y ⪯ K x y\preceq_Kx y⪯Kx,那么 x = y x=y x=y。
- ⪯ K \preceq_K ⪯K对于极限运算是保序的:如果对于 i = 1 , 2 , ⋯ i=1,2,\cdots i=1,2,⋯均有 x i ⪯ K y i x_i\preceq_Ky_i xi⪯Kyi,当 i → ∞ i\rightarrow\infty i→∞时,由 x i → x x_i\rightarrow x xi→x和 y i → y y_i\rightarrow y yi→y,那么 x ⪯ K y x\preceq_Ky x⪯Ky。
最小和极小元
**最小元:**对于每个 y ∈ S y\in S y∈S,均有 x ⪯ K y x\preceq_Ky x⪯Ky ,则称 x ∈ S ,则称x\in S ,则称x∈S是 S S S(关于广义不等式 ⪯ K \preceq_K ⪯K)的最小元。
**最大元:**对于每个 y ∈ S y\in S y∈S,均有 x ⪰ K y x\succeq_Ky x⪰Ky ,则称 x ∈ S ,则称x\in S ,则称x∈S是 S S S(关于广义不等式 ⪯ K \preceq_K ⪯K)的最大元。
**极小元:**如果 y ∈ S , y ⪯ K x y\in S,y\preceq_Kx y∈S,y⪯Kx可以推得 y = x y=x y=x,那么我们称 x ∈ S x\in S x∈S是 S S S上(关于广义不等式 ⪯ K \preceq_K ⪯K)的极小元。
极大元:如果 y ∈ S , y ⪰ K x y\in S,y\succeq_Kx y∈S,y⪰Kx可以推得 y = x y=x y=x,那么我们称 x ∈ S x\in S x∈S是 S S S上(关于广义不等式 ⪯ K \preceq_K ⪯K)的极大元。
分离与支撑超平面
**超平面分离定理:**假设 C C C和 D D D是两个不相交的凸集,即 C ∩ D = ⊘ C\cap D=\oslash C∩D=⊘,那么存在 a ≠ 0 a\neq 0 a=0和 b b b使得超平面 { x ∣ a T x = b } \{x\mid a^Tx=b\} {x∣aTx=b}能够将两个凸集分离。如下图所示。

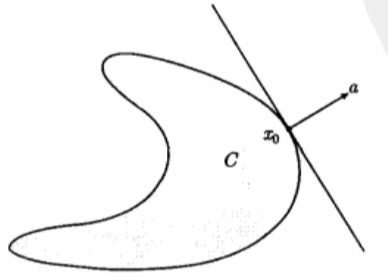
**支撑超平面:**设 C ⊆ R n C\subseteq\mathbf{R}^n C⊆Rn而 x 0 x_0 x0为其边界一点,如果 a ≠ 0 a\neq0 a=0,并且对于任意 x ∈ C x\in C x∈C满足 a T x ≤ a T x 0 a^Tx\le a^Tx_0 aTx≤aTx0,那么称超平面 { x ∣ a T x = a T x 0 } \{x\mid a^Tx= a^Tx_0\} {x∣aTx=aTx0} 为集合 C C C在点 x 0 x_0 x0处的支撑超平面。在几何上表示为超平面 { x ∣ a T x = a T x 0 } \{x\mid a^Tx= a^Tx_0\} {x∣aTx=aTx0}与 C C C相切于点 x 0 x_0 x0,如下图所示:
对偶锥和广义不等式
对偶锥:
K
K
K为一个锥,集合
$$
$$
称为
K
K
K的对偶锥。
K
∗
K^*
K∗总是一个凸锥,即使
K
K
K不是凸锥。从几何上看,
y
∈
K
∗
y\in K^*
y∈K∗当且仅当
−
y
-y
−y是
K
K
K在原点的一个支撑超平面的法线,如下图所示:

性质
-
K ∗ K^* K∗是闭凸锥。
-
K 1 ⊆ K 2 K_1\subseteq K_2 K1⊆K2可以导出 K 2 ∗ ⊆ K 1 ∗ K_{2}^*\subseteq K_1^* K2∗⊆K1∗。
-
如果 K K K由非空内部,那么 K ∗ K^* K∗是尖的(不含直线)。
-
如果 K K K的闭包是尖的,那么 K ∗ K^* K∗有非空内部。
-
K ∗ ∗ K^{**} K∗∗是 K K K的凸包的闭包。(因此,如果 K K K是凸和闭得,则 K ∗ ∗ = K K^{**}=K K∗∗=K)。
-
如果 K K K是一个正常锥,那么它的对偶 K ∗ K^{*} K∗也是,进一步将, K ∗ ∗ = K K^{**}=K K∗∗=K。
不是凸锥。从几何上看, y ∈ K ∗ y\in K^* y∈K∗当且仅当 − y -y −y是 K K K在原点的一个支撑超平面的法线,如下图所示:
[外链图片转存中…(img-iMHjGdPV-1692066222841)]
性质
-
K ∗ K^* K∗是闭凸锥。
-
K 1 ⊆ K 2 K_1\subseteq K_2 K1⊆K2可以导出 K 2 ∗ ⊆ K 1 ∗ K_{2}^*\subseteq K_1^* K2∗⊆K1∗。
-
如果 K K K由非空内部,那么 K ∗ K^* K∗是尖的(不含直线)。
-
如果 K K K的闭包是尖的,那么 K ∗ K^* K∗有非空内部。
-
K ∗ ∗ K^{**} K∗∗是 K K K的凸包的闭包。(因此,如果 K K K是凸和闭得,则 K ∗ ∗ = K K^{**}=K K∗∗=K)。
-
如果 K K K是一个正常锥,那么它的对偶 K ∗ K^{*} K∗也是,进一步将, K ∗ ∗ = K K^{**}=K K∗∗=K。