在当今数字化时代，企业拥有海量数据，这些数据散落在不同部门、系统和平台之间，形成了所谓的“数据孤岛”。要想实现数据的最大化价值，就必须解决数据集成与流动的挑战。本文将深入探讨数据集成与流动优化的重要性，以及如何通过这一过程来解锁企业数据的无限潜力。

一、数据集成：拼图的开始

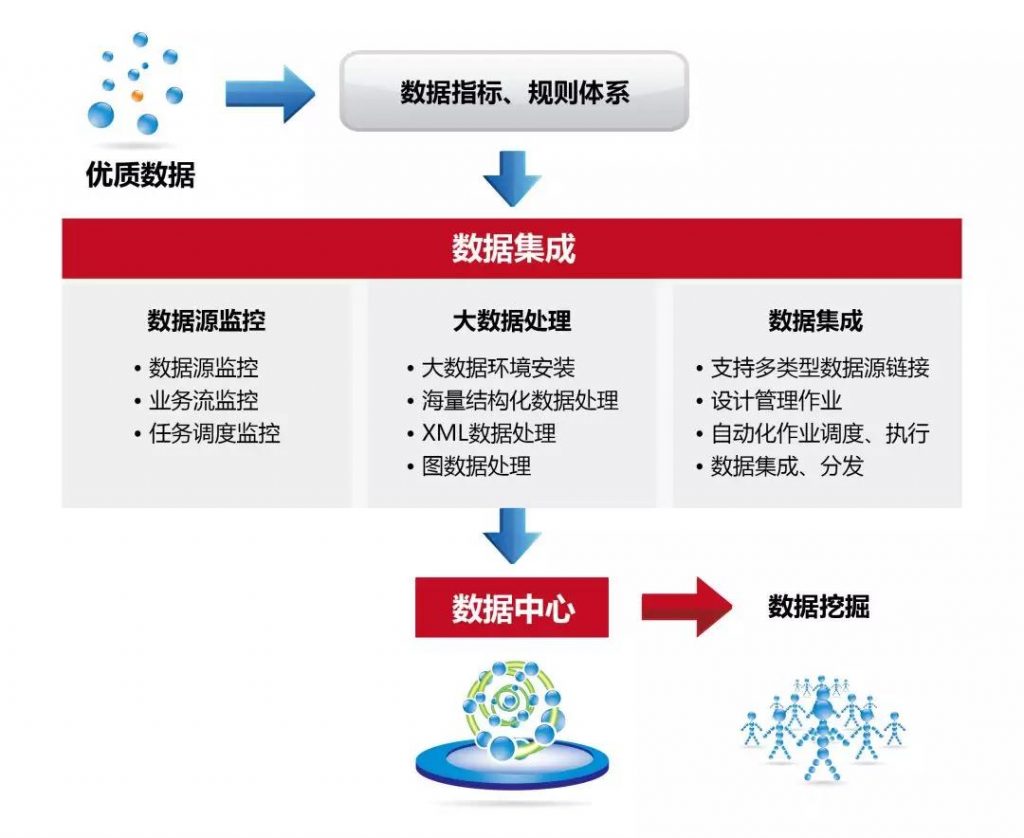
数据集成是将来自不同源头的数据整合到一个统一的视图中的过程。它是实现数据流动优化的基础，类似于拼图的开始。通过数据集成，企业能够消除数据孤岛，让数据能够在不同部门和系统之间自由流动，从而实现更高效的业务流程和决策。

1、跨越隔阂： 数据集成能够将分散的数据汇聚在一起，使得不同部门之间能够更好地合作和协同，共同推动业务创新。

2、数据一体化： 通过数据集成，企业可以获得全面、一致的数据视图，从而为决策提供更可靠的数据支持。

编辑搜图

二、数据流动优化：顺畅的流动路径

一旦数据集成完成，接下来就需要优化数据的流动过程，确保数据能够以高效和无阻碍的方式在企业内外流动。这就好比拼图完成后，顺畅的流动路径能够让每个数据碎片都能够到达它需要去的地方。

1、实时数据： 数据流动的优化意味着数据能够实时地从一个部门或系统传输到另一个部门或系统，从而支持实时的决策和操作。

2、自动化流程： 优化数据流动还包括自动化流程的引入，使得数据能够按照设定的规则自动传输，减少了人为的干预，提高了数据传输的速度和准确性。

三、解锁无限潜力：实际案例

一个以数据为核心的零售企业，通过数据集成与流动优化，实现了数据的无限潜力。他们将来自线上、线下、供应链等不同渠道的数据进行集成，使得销售、库存、订单等信息能够实时共享。通过优化数据流动，他们能够更快速地响应市场变化，调整库存，提升了客户满意度。

编辑搜图

四、结论

数据集成与流动优化是解锁企业数据无限潜力的关键步骤。通过消除数据孤岛，优化数据流动，企业可以获得更高效的业务流程、更准确的决策，从而实现业务增长和创新。在数字化转型的浪潮中，不断提升数据集成与流动优化的能力，将成为企业保持竞争优势的重要因素。

免费获取解决方案，点击前往~

由此极力推荐FineDataLink，它能将不同源的数据整合到一个统一的平台上，通过强大的数据转换和清洗功能，确保数据的准确性和一致性。其先进的元数据管理系统有助于解决数据语义问题，使不同团队对数据的理解保持一致。此外，FineDataLink提供实时数据集成和更新功能，保持数据的时效性和实时性。