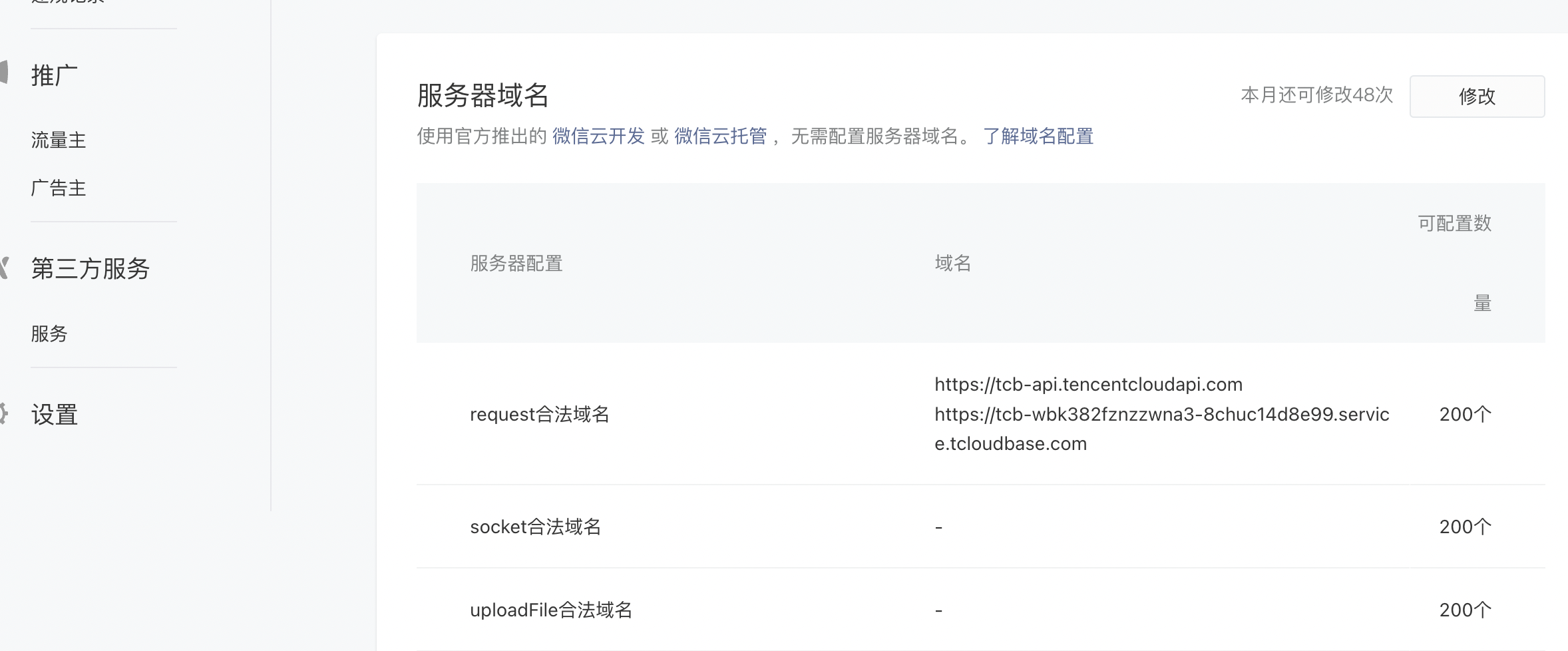
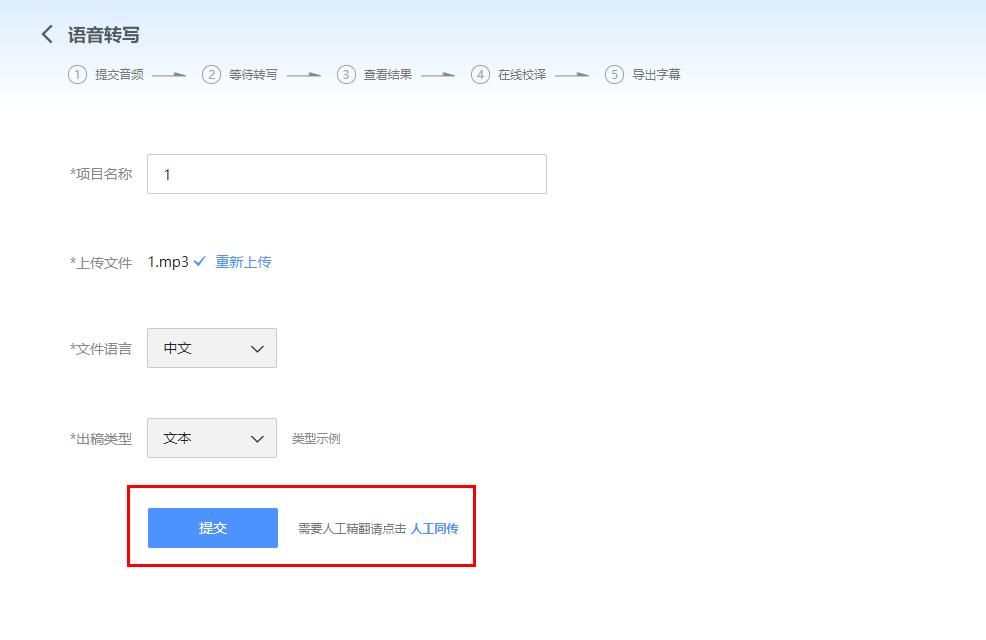
牛客上的三道反转链表的题,入门题,反转链表有很多种做法,本来做第一题的时候是随便写了一种,然后后面发现我用的方法,在做第二题第三题的时候有点繁琐,所以就把三道题一起考虑了一下,选了一种相对更加清晰的思路。三道题使用同一思路解决。
反转链表
题目
反转链表-题目链接
给定一个单链表的头结点pHead(该头节点是有值的,比如在下图,它的val是1),长度为n,反转该链表后,返回新链表的表头。
思路
方法就是使用三个指针来逆转链表指向
cur指针指向当前节点,pre指向前驱,temp指向后继。
操作如图所示:
初始状态时,pre初始化为NULL
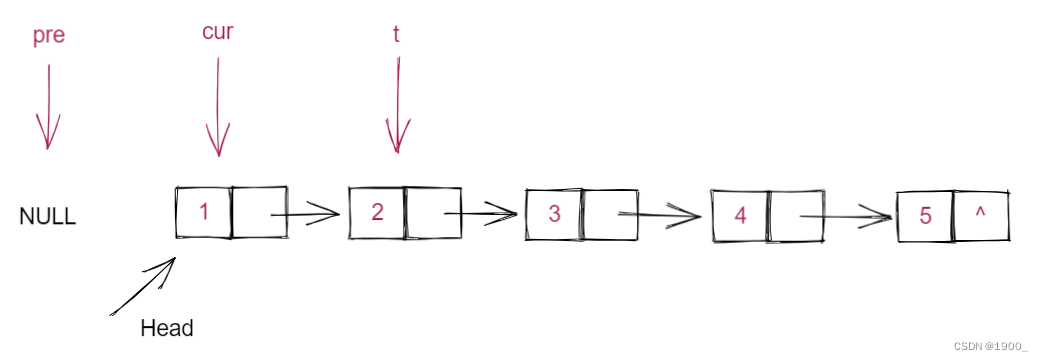
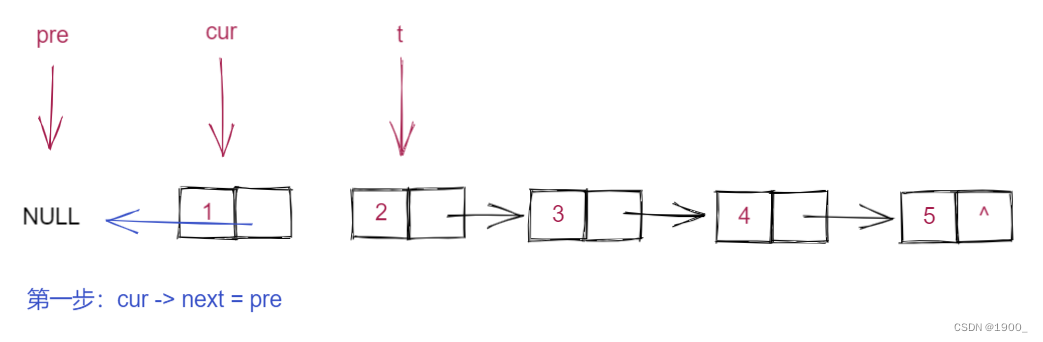
第一步:指针回指
第二步:三个指针前移
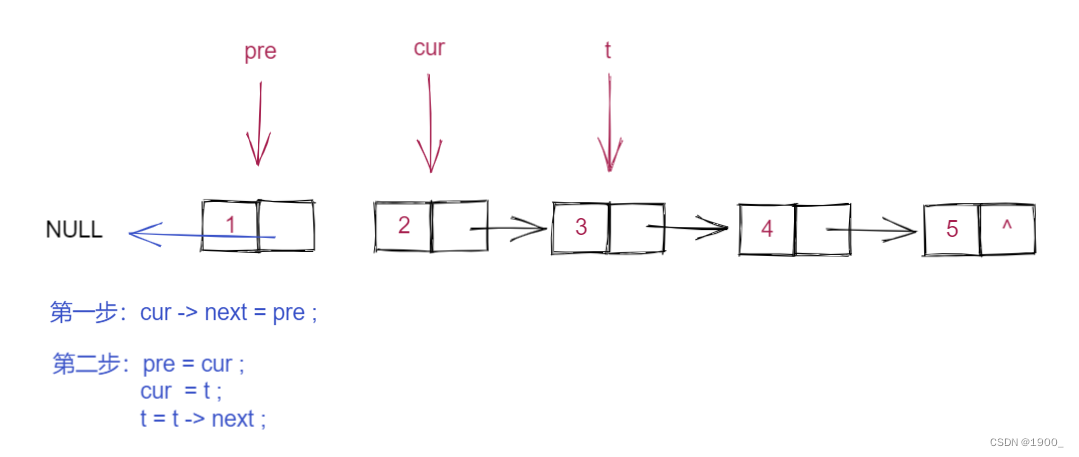
然后循环这两步,一直到最后即可将整个链表反转。
代码实现
时间复杂度:O(n)
空间复杂度:O(1)
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};*/
class Solution {
public:
ListNode* ReverseList(ListNode* pHead) {
struct ListNode* cur =pHead;
struct ListNode* pre = NULL;
struct ListNode* temp = cur->next;
while(cur!=NULL){
cur->next = pre;
pre = cur;
cur = temp;
temp = temp->next;
}
return pre;
}
};
链表内指定区间反转
题目
指定区间反转-题目链接
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转,要求时间复杂度 O(n),空间复杂度 O(1)。
思路
我们先找到第m个结点,然后从m到n,我们还是按照上一题的思路用三个指针将其逆置。
但是需要注意的是:我们光找到第m个结点还不够,还应该保留m的前驱结点,这样方便逆置完了之后链接回主链。
因此我们遍历的时候,用cur当作遍历指针,用pre当作前驱指针。
由于首元节点没有前驱,所以我们增加一个虚拟节点,使操作统一,不需要单独考虑首节点的特殊情况。
当我们遍历到第m个结点的时候,这时候pre保持不动,然后使用cur指针和p指针和t指针来进行逆置操作。一直逆置到第n个结点。
然后将逆置完的链表链接回主链表。
如图所示,是表长=5,m=2,n=4的情况
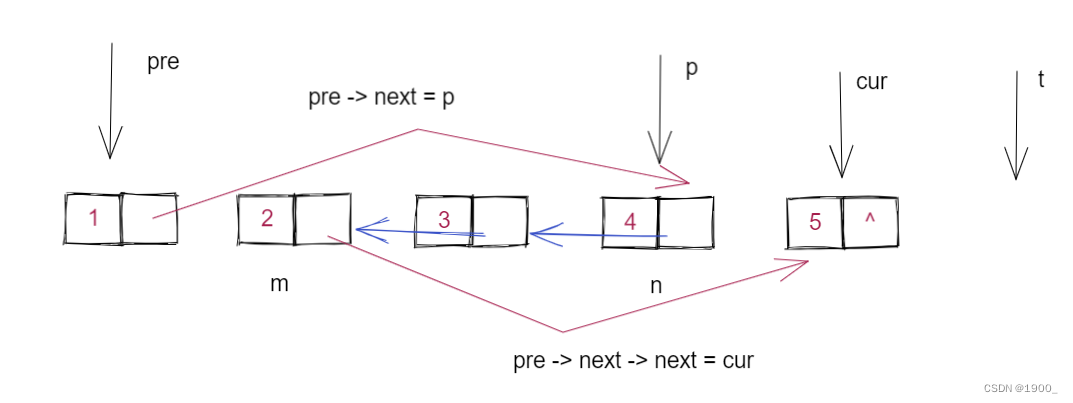
另外还需要注意一点:按照这个方法,我们最后返回head即可。但是有一种情况特殊,如果m=1,也就是说第一个开始就开始反转,那么head所指向的结点反转后就是最后一个结点了,所以不能返回head,应该返回pre->next。所以代码中这一步需要特殊处理。
代码
时间复杂度:O(n)
空间复杂度:O(1)
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
class Solution {
public:
/**
*
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
ListNode* reverseBetween(ListNode* head, int m, int n) {
// write code here
ListNode* pre = new ListNode(-1);
pre -> next = head;//增加一个前驱节点
ListNode* cur = head;
for (int i = 1; i < m; i++) {
pre = cur;
cur = cur->next;
}
ListNode* p = NULL;
ListNode* t = cur->next;
for (int i = m; i <= n; i++) {
cur->next = p;//回指
p = cur;
cur = t;
t = t->next;
}
pre->next->next = cur;//链接回主链
pre->next = p;
if (m == 1) head = pre->next;
return head;
}
};
链表中的结点每k个一组反转
题目
链表中的结点每k个一组反转-题目链接
将给出的链表中的节点每 k 个一组翻转,返回翻转后的链表
如果链表中的节点数不是 k 的倍数,将最后剩下的节点保持原样
你不能更改节点中的值,只能更改节点本身。
思路
根据我们前面两题的思路,我们反转任何一段链表,只需要用到三个条件:待反转链表的第一个结点,第一个结点的前驱,反转数量。
如图,如果我们要反转这一段链表只需要知道这三个条件即可
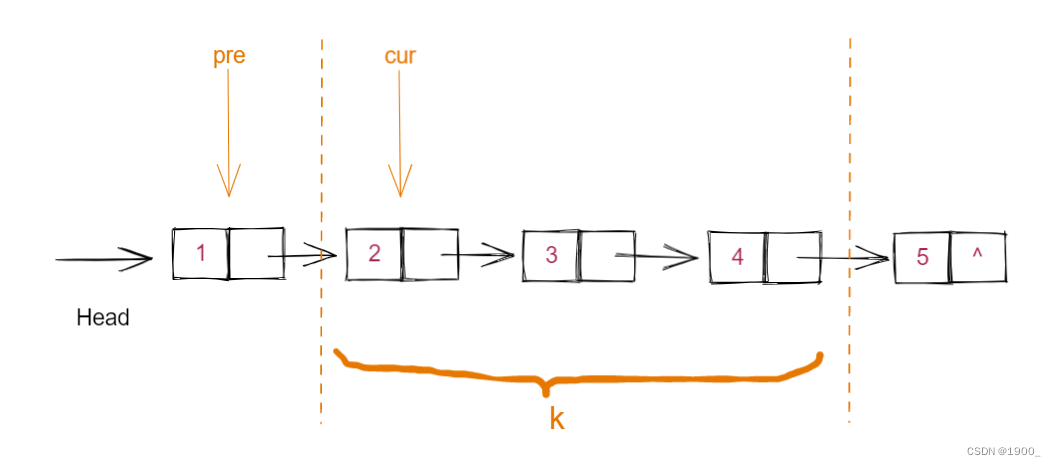
代码如下,基本上就是上一题的思路:
void reverse(ListNode* pre, ListNode* cur, int k) {
ListNode* head = pre;//把头保留下来 反转后链接的时候需要用到
pre = NULL;//三个指针 开始反转
ListNode* t = cur->next;
for (int i = 1; i <= k; i++) {//限制反转数量为k
cur->next = pre;
pre = cur;
cur = t;
t = t->next;
}
//反转后 链接回主链
head ->next->next = cur;
head->next = pre;
}
那么这个操作实现了,现在题目就简单了,每k个一组就反转,我们就遍历链表,用一个num来计数
当num=1的时候,记录下前驱pre和当前位置cur,然后当num到k的时候,说明这一段要需要反转
这一段链表的头结点以及其前驱我们都有,那就可以用这个子函数实现反转了。
假设:k=4,那么如图所示,cur指的是当前结点,已经到第四个了,cur_t和pre_t是我们保存的这一段链表的头和头的前驱
所以我们将其交给函数,反转,反转完成后,如下图所示。
这里需要注意一个点:反转前cur指向第四个结点,既然前四个反转了,那么反转之后,cur就应该指向结点1才对。
所以反转之后,我们要纠正cur的指向。(注意,只需要纠正cur的指向,不需要纠正pre,因为反转完,结点4也遍历完了,马上就指针后移了,pre直接等于纠正后的cur即可,然后cur后移即可。)

另外还有个问题,与上一个题目相同的问题,那就是第一组反转的链表,需要将head重置一下,不然返回head会出错。
代码
时间复杂度:O(n)
空间复杂度:O(1)
(这整个操作最坏情况下,相当于遍历了两遍链表,也就是2n,复杂度还是O(n))
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* };
*/
class Solution {
public:
/**
*
* @param head ListNode类
* @param k int整型
* @return ListNode类
*/
void reverse(ListNode* pre, ListNode* cur, int k) {
ListNode* head = pre;
pre = NULL;
ListNode* t = cur->next;
for (int i = 1; i <= k; i++) {
cur->next = pre;
pre = cur;
cur = t;
t = t->next;
}
//反转后 连接回主链
head ->next->next = cur;
head->next = pre;
}
ListNode* reverseKGroup(ListNode* head, int k) {
// write code here
ListNode* pre = new ListNode(-1);
pre->next = head; //增加一个新的结点
ListNode* cur = head;
ListNode* cur_t = NULL;//保存待反转链表的头和前驱
ListNode* pre_t = NULL;
int flag = 1;//标记 第一组反转时 需将head重置
int num = 1;
while (cur != NULL) {
if (num == 1) {//保存待反转链表的头和前驱
cur_t = cur;
pre_t = pre;
}
if (num % k == 0) {
if (flag) { //第一次反转
head = cur;
flag = 0;
}
reverse(pre_t, cur_t, k);
//反转完成后 纠正cur指针位置
cur = cur_t;
num = 0;//计数置0
}
pre = cur;
cur = cur->next;
num++;
}
return head;
}
};
![[附源码]Python计算机毕业设计二手图书回收销售网站Django(程序+LW)](https://img-blog.csdnimg.cn/1d6a772a1f63413faf4809633c39385d.png)