2023-03-11 美团机试

题目：美团2024届暑期实习第一轮后端笔试详解
通过了前三道，花了一堆时间在第四道上，一分没得，第五题都没时间看。题目的设置有点无语，一到四题安排在一起，第五题安排在一起，当时不知道提交后可以继续修改，进了一到四题的项就不敢提交，以为第五题单独放一起肯定很难，最后没时间了看了一下第五题，比较简单。搞不明白为啥要把第五题单独列一个项，要不然怎样都能写出四道来

第一题

小美有一个由数字字符组成的字符串。现在她想对这个字符串进行一些修改。 具体地，她可以将文个字符串中任意位置字符修改为任意的数字字符。她想知道，至少进行多少次修改，可以使得“修改后的字符串不包含两个连续相同的字符?
例如，对于字符串”111222333", 她可以进行3次修改将其变为” 121212313"。输入描述
一行，一个字符串s，保证s只包含数字字符。1<=|s|<= 100000输出描述
一行，一个整数，表示修改的最少次数。

思路
简单题，遇见相同的字符直接改成数字字符之外的‘a’即可

#include <bits/stdc++.h>
using namespace std;

int main() {
  string s;
  while (cin >> s) {
    int cnt = 0;
    for (int i = 1; i < s.length(); i++) {
      if (s[i] == s[i - 1]) {
        s[i] = 'a';
        cnt++;
      }
    }
    cout << cnt << endl;
  }
}

第二题

小团在一个n*m的网格地图上探索。 网格地图上第i行第j列的格子用坐标(i,j)简记。初始时，小团的位置在地图的左上角，即坐标(1,1)。 地图上的每个格子 上都有一定的金币， 特别地，小团位于的初始位置(1,1)上的金币为0。小团在进行探索移动时，可以选择向右移动-格(即从(x,y)到达(x,y+1))或向下移动一格(即从(x,y)到达(x+1,y)) 。地图上的每个格子都有一个颜色，红，色或蓝色。如果小团次移动前后的两个格子颜色不同，那么他需要支付k个金币才能够完成这-次移动;如果移动前后的两个格子颜色相同，则不需要支付金币。小团可以在任意格子选择结束探索。现在给你网格地图上每个格子的颜色与金币数量，假设小团初始时的金币数量为0，请你帮助小团计算出最优规划，使他能获得最多的金币，输出能获得的最多 金币数量即可。注意:要求保证小团任意时刻金币数量不小于零。

输入描述
第一行是三个用空格隔开的整数n、m和k，表示网格地图的行数为n,列数为m,在不同颜色的两个格子间移动需要支付k个金币。
接下来n行，每行是一个长度为m的字符串， 字符串仅包含字符R’或’ B’。第i行字符串的第j个字符表示地图上第i行第j列的格子颜色，如果字符为’ R’ 则表示格子颜色为红色，为’B’ 表示格子颜色为蓝色。
接下来是个n行m列的非负整数矩阵，第i行第j列的数字表示地图上第行第j列的格子上的金币数量。保证所有数据中数字大小都是介于[0, 10]的整数。
1<=n,m<=200, 1<=k<=5。

思路
刚开始直接暴力回溯，运行超时

#include <bits/stdc++.h>
using namespace std;

// 定义全局变量
string color[201];
int coin_num[201][201];
int n, m, k;
int max_coin_num;

void dfs(int x, int y, int cur_coin_num) {
  max_coin_num = max(max_coin_num, cur_coin_num);
  if (x + 1 < n) {  // 向下移动
    int offer = color[x][y] == color[x + 1][y] ? 0 : -k;
    if (cur_coin_num + offer >= 0) {
      dfs(x + 1, y, cur_coin_num + offer + coin_num[x + 1][y]);
    }
  }
  if (y + 1 < m) {  // 向右移动
    int offer = color[x][y] == color[x][y + 1] ? 0 : -k;
    if (cur_coin_num + offer >= 0) {
      dfs(x, y + 1, cur_coin_num + offer + coin_num[x][y + 1]);
    }
  }
}
int main() {
  while (cin >> n >> m >> k) {
    for (int i = 0; i < n; i++) {
      cin >> color[i];
    }
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        cin >> coin_num[i][j];
      }
    }
    max_coin_num = 0;
    dfs(0, 0, 0);
    cout << max_coin_num << endl;
  }
}

后面用动态规划写了一个版本，通过

#include <bits/stdc++.h>
using namespace std;

int main() {
  string color[201];
  int coin_num[201][201];
  int n, m, k;
  while (cin >> n >> m >> k) {
    for (int i = 0; i < n; i++) {
      cin >> color[i];
    }
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        cin >> coin_num[i][j];
      }
    }
    int ans = 0;
    vector<vector<int>> max_coin_num(n, vector<int>(m, -1));  // 全部设成-1，不可达
    max_coin_num[0][0] = 0;
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        int value = -1;
        if (i - 1 >= 0) {  // 从上方转移而来
          int offer = color[i][j] == color[i - 1][j] ? 0 : -k;
          value = max(value, max_coin_num[i - 1][j] + offer);
        }
        if (j - 1 >= 0) {  // 从左边转移而来
          int offer = color[i][j] == color[i][j - 1] ? 0 : -k;
          value = max(value, max_coin_num[i][j - 1] + offer);
        }
        if (value >= 0) {  // 进行状态转移
          max_coin_num[i][j] = value + coin_num[i][j];
        }
      }
    }
    // 计算最大金币数目
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        ans = max(ans, max_coin_num[i][j]);
      }
    }
    cout << ans << endl;
  }
}

第三题

小美是位天文爱好者， 她收集了接下来段时间中所有 会划过她所在的观测地上空的流星信息。具体地，她收集了n个流星在她所在观测地上空的出现时刻和消失时刻。对于一个流星，若’其的出现时刻为s，消失时刻为t，那么小美在时间段[s, t]都能够观测到它。对于一个时刻，观测地上空出现的流星数量越多，则小美认为该时刻越好。小美希望能够选择一个最佳的时刻进行观测和摄影，使她能观测到最多数量的流星。现在小美想知道 ，在这个最佳时刻，她最多能观测到多少个流星以及一共有多少个最佳时刻可供她选择。

输入描述
第一行是一个正整数n,表示流星的数量。
第二行是n个用空格隔开的正整数，第i个数si表示第i个流星的出现时间。
第三行是n个用空格隔开的正整数，第i个数ti表示第i个流星的消失时间。
1<=n<=100000, 1<=si<=ti<=10^9
输出描述
输出一行用空格隔开的两个数x和y,其中x表示小美能观测到的最多流星数，y表示可供她选择的最佳时刻数量。

思路
排序，从左往右计算可观测的流星数量，不过后面看别人说标准解法是差分数组

#include <bits/stdc++.h>
using namespace std;

struct Node {
  int value;      // 时间
  bool is_start;  // 是否为起始观测时间
  int number;     // 观测流星数目
};

int main() {
  int n, s, t;
  while (cin >> n) {
    vector<Node> star(2 * n);
    for (int i = 0; i < n; i++) {
      cin >> s;
      star[i].value = s;
      star[i].is_start = true;
    }
    for (int i = n; i < 2 * n; i++) {
      cin >> t;
      star[i].value = t;
      star[i].is_start = false;
    }
    auto cmp = [&](const Node& n1, const Node& n2) -> bool { return n1.value < n2.value || (n1.value == n2.value && n1.is_start == true); };  // 尽可能让起始观测时间在终止观测时间之前
    sort(star.begin(), star.end(), cmp);
    int observer = 0;
    int max_observer = 0;
    for (int i = 0; i < 2 * n; i++) {
      if (star[i].is_start) {  // 遇到起始时间，观测数加一
        observer++;
        star[i].number = observer;
      } else {  // 遇到终止时间，当前观测数不变，之后观测数减一
        star[i].number = observer;
        observer--;
      }
      max_observer = max(max_observer, star[i].number);
    }
    int time_num = 0;
    for (int i = 0; i < 2 * n; i++) {
      if (star[i].number == max_observer) {  // 一定为start-end组合，跳过end节点
        time_num += star[i + 1].value - star[i].value + 1;
        i++;
      }
    }
    cout << max_observer << " " << time_num << endl;
  }
}

第四题

小D和小W最近在玩坦克大战，双方操控自己的坦克在16*1 6的方格图上战斗，小D的坦克初始位置在地图的左上角，朝向为右，其坐标(0,0)， 小W的坦克初始位置在地图右下角，朝向为左，坐标为(15,15)。坦克不能移动到地图外，坦克会占领自己所在的格子，己方的坦克不可以进入对方占领过的格子。每一个回合双方必须对自己的坦克下达以下5种指令中的一种:
.移动指令U:回合结束后，使己方坦克朝向为上，若上方的格子未被对方占领，则向当前朝向移动一个单位(横坐标-1)，否则保持不动;
.移动指令D:回合结束后，使己方坦克朝向为下，若下方的格子未被对方占领，则向当前朝向移动一个单位(横坐标+1)，否则保持不动，
.移动指令L:回合结束后，使己方坦克朝向为左,若左侧的格子未被对方占领，则向当前朝向移动一个单位(纵坐标-1) ,否则保持不动;
.移动指令R:回合结束后，使己方坦克朝向为右，若右侧的格子未被对方占领，则向当前朝向移动一个单位(纵坐标+1)，否则保持不动;
. 开火指令F:己方坦克在当前回合立即向当前朝向开火;

己方坦克开火后，当前回合己方坦克的正前方若有对方的坦克，对方的坦克将被摧毁，游戏结束，己方获得胜利;若双方的坦克在同一-回合被摧毁，游戏结束，判定为平局;若双方的坦克在同一回合内进入到同一个未被占领的格子，则双方的坦克发生碰撞，游戏结束，判定为平局;当游戏进行到第256个回合后，游戏结束，若双方坦克均未被摧毁，则占领格子数多的一方获得胜利，若双方占领的格子数一样多，判定为平局。*注意， 若-方开火， 另-方移动，则认为是先开火，后移动。

现在小D和小W各自给出一串长度为256的指令字符串， 请你帮助他们计算出游戏将在多少个回合后结束，以及游戏的结果。

输入描述
输入共两行，每行为一串长度为256的指令宁符串，字符串中只包含“U”，“D"，“L" “R”，“F"这五个字符。第一行表示小D的指令，第工行表示小W的指令。
输出描述
输出一共两行，第一行一个整数k，表示游戏将在k个回合后结束。第二行为游戏的结 果，若小D获胜则输出“D"，若小W获胜则输出“W”若平局则输出“P”

思路
大模拟，40分钟一分没得，懒得贴代码了

第五题

给一棵有n个点的有根树，点的编号为1到n，根为1。每个点的颜色是红色或者蓝色。对于树上的一个点，如果其子树中(不包括该点本身)红色点和蓝色点的数量相同，那么我们称该点是平衡的。

请你计算给定的树中有多少个点是平衡点。

输入描述
第一行是一个正整数n，表示有n个点。
接下来行一个长度为n的字符串，仅包含字符R’和’B’， 第i个字符表示编号为的节点的颜色，字符为’R’ 表示红色，’ B’ 表示蓝色。
接下来一行n-1个用空格隔开的整数，第1个整数表示编号为i+ 1的点的父亲节点编号。1<=n<=10000

输出描述
一行一个整数，表示树上平衡点的个数。

思路
没写，无语的题目安排

2023-03-12 拼多多机试

题目链接： 2023暑期实习-笔试-拼多多-算法实习生
晚上的笔试，过了三道半

第一题 多多的压缩编码II

还原压缩后的字符串
输入 10a1b1c
输出 aaaaaaaaaabc

思路
简单题

#include <bits/stdc++.h>
using namespace std;

int main() {
  string s;
  while (cin >> s) {
    string ans = "";
    int number = 0;
    for (char c : s) {
      if (c >= '0' && c <= '9') {  // 遇见数字
        number = number * 10 + c - '0';
      } else {                     // 遇见字母
        ans += string(number, c);  // 添加number个字符c
        number = 0;
      }
    }
    cout << ans << endl;
  }
}

第二题 多多的飞机大战游戏

多多最近下载了一款飞机大战的游戏，多多可以通过游戏上的不同发射按键来控制飞机发射子弹：
按下A键，飞机会发射出2枚子弹，每个子弹会对命中的敌人造成1点固定伤害，但不能作用于同个敌人。
按下B键，飞机会发射出1枚子弹，子弹会对命中的敌人造成巨额伤害并瞬间将其秒杀。

多多是个游戏高手，总是能操控子弹命中想要命中的敌人。这个游戏—共有 T 个关卡，消灭当前关卡全部敌人后，发射出去多余的子弹会消失，游戏会自动进入下一个关卡。
假设每个关卡都会在屏幕中同时出现N个敌人，这N个敌人所能承受的伤害也已经知道。多多想知道，每个关卡自己最少按几次发射按键就可以将敌人全部消灭。
输入描述
第一行输入一个固定数字T（1<=T=1000）表示关卡的总数量，N（1<=N<=200）表示每个关卡出现的敌人数量。
接下来T行，每行有N个数字D1，D2，…，Dw（1<= Di <= 200）分别表示这N个敌人所能承受的伤害。

输出描述
结果共有N行，每行一个数字，分别表示对于这个关卡，最少按几次发射按键就可以将敌人全部消灭。

思路
承受伤害为1按A键，大于1则直接按B键

#include <bits/stdc++.h>
using namespace std;

int main() {
  int t, n;
  while (cin >> t >> n) {
    for (int i = 0; i < t; i++) {
      int di;
      unordered_map<int, int> cnt;  // 承受伤害敌人与相应数目
      for (int j = 0; j < n; j++) {
        cin >> di;
        cnt[di]++;
      }
      int ans = 0;
      for (auto& [damage, num] : cnt) {
        if (damage == 1) {       // 全部选择A键
          ans += (num + 1) / 2;  // 向上取整
        } else {                 // 全部选择B键
          ans += num;
        }
      }
      cout << ans << endl;
    }
  }
}

第三题 多多的团建计划

多多君准备了三个活动（分别编号A、B和C)，每个活动分别有人数上限以及每个人参加的费用。
参加团建的有N个人(分别编号1~N），每个人先投票选择若干个意向的活动，最终每个人只能参加其中一个。
多多君收集完投票结果后，发现如何安排成为了大难题：如何在满足所有人的意向的情况下，使得活动的总费用最少。
于是多多君找到了擅长编程的你，希望你能帮助找到个合理的团建计划。

输入描述
第一行，一个整数N（1<=N<=100），代表准备参加活动的人数。
接下来N行，每行一个由 “ABC” 组成的字符串，其中第i行表示第i个人投票了哪几个活动。输入保证字符串非空，且由大写的 “ABC” 字符组成。
最后三行，每行两个整数，分别表示三个活动的人数上限以及每个人参加的费用。
输出描述
输出共2行
如果能满足所有人的要求，第一行输出 “YES”，第二行输出最少的总费用。
如果不能满足所有人的要求，第一行输出 “NO”，第二行输出最多能满足多少人。

思路
本来想用贪心，但觉得贪心策略不一定对，就直接用dfs暴力枚举所有可能了，好像得了40-60分，太久了，忘了
但使用贪心虽然得不到满分，也有80-90分了，不能一昧地暴力回溯

#include <bits/stdc++.h>
using namespace std;

// 全局变量
const int kINf = 1 << 30;
int n;
vector<string> vote(101);  // 每个人投票的活动
vector<int> limit(3);      // 活动限制
vector<int> money(3);      // 活动费用
int min_total;             // 最小总费用
int max_require;           // 最多满足多少人
bool can_all_require;      // 是否能满足

int get_money(const vector<int>& origin_limit, const vector<int>& cur_limit) {  // 通过活动名额差值计算总费用
  int total_money = 0;
  for (int i = 0; i < 3; i++) {
    total_money += (origin_limit[i] - cur_limit[i]) * money[i];
  }
  return total_money;
}

bool is_all_zero(const vector<int>& cur_limit) { return cur_limit[0] == 0 && cur_limit[1] == 0 && cur_limit[2] == 0; }  // 活动是否全部参加完

void dfs(int cur_index, vector<int> cur_limit, int cur_require) {
  if (cur_index >= n || is_all_zero(cur_limit)) {               // 当前下标越界或活动全部参加完
    if (cur_require == n) {                                     // 已经满足所有人
      min_total = min(min_total, get_money(limit, cur_limit));  // 计算最小总费用
      can_all_require = true;                                   // 可以满足所有人
    } else {
      max_require = max(max_require, cur_require);  // 计算最多满足人数
    }
    return;
  }
  if (vote[cur_index].length() == 1) {  // 如果只有一个人（好像和下面的代码冗余了，不知道我当时怎么想的）
    char c = vote[cur_index][0];
    if (cur_limit[c - 'A'] > 0) {  // 当前活动尚有名额
      cur_limit[c - 'A']--;
      dfs(cur_index + 1, cur_limit, cur_require + 1);
      cur_limit[c - 'A']++;
    } else {
      if (can_all_require) {  // 已经存在满足所有人的选择，略过当前选择
        return;
      }
      dfs(cur_index + 1, cur_limit, cur_require);  // 不考虑该人
    }
  } else {
    for (char c : vote[cur_index]) {  // 依次选择各个活动
      if (cur_limit[c - 'A'] > 0) {
        cur_limit[c - 'A']--;
        dfs(cur_index + 1, cur_limit, cur_require + 1);
        cur_limit[c - 'A']++;
      }
    }
    if (can_all_require) {  // 已经存在满足所有人的选择，略过当前选择
      return;
    }
    dfs(cur_index + 1, cur_limit, cur_require);  // 不考虑该人
  }
}

int main() {
  while (cin >> n) {
    for (int i = 0; i < n; i++) {
      cin >> vote[i];
    }
    for (int i = 0; i < 3; i++) {
      cin >> limit[i] >> money[i];
    }

    min_total = kINf;
    max_require = 0;
    can_all_require = false;
    dfs(0, limit, 0);
    if (min_total == kINf) {  // 不能满足所有人
      cout << "NO" << endl << max_require << endl;
    } else {  // 可以满足所有人
      cout << "YES" << endl << min_total << endl;
    }
  }
}

第四题 多多的餐厅客流量

多多君开了一家自助餐厅，为了更好地管理库存，多多君每天需要对之前的客流量数据进行分析，并根据客流量的平均数和中位数来制定合理的备货策略。
输入描述
第一行一个整数N,表示餐厅营业总天数(0<n<=200,000),< p=“”></n<=200,000),<>
第二行共N个整数,分别表示第i天的客流量R:(0= R:1, 000, 000)。

输出描述
输出共两行：
第一行长度为N，其中第i个值表示前i天客流量的平均值；第二行长度为N，其中第i个值表示前i天客流量的中位数。
一共有N天，每天的客流量为 Ri，求第1天到第i天的平均数和中位数，结果四舍五入保留整数。

思路
没啥思路，就用插入排序过了，标准方法是295. 数据流的中位数

#include <bits/stdc++.h>
using namespace std;

int GetInterge(double d) {  // 四舍五入
  int n = d;
  double test = n + 0.5;
  if (d >= test) {
    return n + 1;
  }
  return n;
}
void InsertSort(vector<int>& vec, int val) {  // 借助二分查找实现插入排序
  auto iter = upper_bound(vec.begin(), vec.end(), val);
  vec.emplace(iter, val);
}

int main() {
  int n;
  while (cin >> n) {
    vector<int> vec;
    vector<int> avg(n + 1);
    vector<int> mid(n + 1);
    double sum = 0;
    for (int i = 1; i <= n; i++) {
      int r;
      cin >> r;
      sum += r;
      avg[i] = GetInterge(sum / i);  // 求平均值
      InsertSort(vec, r);
      double tmp = vec[i / 2] + vec[(i - 1) / 2];
      mid[i] = GetInterge(tmp / 2);  // 求中位数
    }
    // 输出结果
    for (int i = 1; i <= n; i++) {
      cout << avg[i] << " ";
    }
    cout << endl;
    for (int i = 1; i <= n; i++) {
      cout << mid[i] << " ";
    }
    cout << endl;
  }
}

2023-3-15 阿里机试

题目链接: 大厂真题|3月15日阿里春招笔试三道题
晚上的笔试，七道单选，八道多选，三道编程题，编程题过了2道半，不能使用本地IDE，故没当时的代码（临结束的时候应该把所有的代码拷贝到剪切板的）

第一题

思路
满二叉树，首先根据数组构建二叉树，而后寻找根节点，最后递归求解满二叉树，仅当两个子树皆为满二叉树且节点数目相同时该树为满二叉树

按记忆打的，不一定对

#include <bits/stdc++.h>
using namespace std;

struct TreeNode {
  TreeNode* left;
  TreeNode* right;
  TreeNode() : left(nullptr), right(nullptr) {}
};
using Result = pair<int, bool>;  // 节点数量-是否为满二叉树

Result GetNodeInfo(TreeNode* node, int& full_node_num) {
  if (node == nullptr) {  // 空节点
    return {0, true};
  }
  Result left_info = GetNodeInfo(node->left, full_node_num);
  Result right_info = GetNodeInfo(node->right, full_node_num);
  bool is_full = (left_info.first == right_info.first) && left_info.second && right_info.second;  // 两个子节点均为满二叉树且节点数目一致
  int nodes = left_info.first + right_info.first + 1;
  if (is_full) {  // 满二叉树节点加一
    full_node_num++;
  }
  return {nodes, is_full};
}

int main() {
  int n;
  while (cin >> n) {
    vector<TreeNode> tree_node(n + 1);  // 树节点
    vector<bool> appear(n + 1, false);  // 节点是否出现在输入中
    // 构建二叉树
    for (int i = 1; i <= n; i++) {
      int x, y;
      cin >> x >> y;
      if (x != -1) {
        tree_node[i].left = &tree_node[x];
        appear[x] = true;
      }
      if (y != -1) {
        tree_node[i].right = &tree_node[y];
        appear[y] = true;
      }
    }
    // 寻找根节点（未出现的节点）
    int root = 0;
    for (int i = 1; i <= n; i++) {
      if (!appear[i]) {
        root = i;
        break;
      }
    }
    // 计算满二叉树节点数目
    int ans = 0;
    GetNodeInfo(&tree_node[root], ans);
    cout << ans << endl;
  }
}

/*
5
2 3
4 5
-1 -1
-1 -1
-1 -1
*/

第二题

三个数最大值减最小值=1，使用map记录数组与出现次数，对每个数字处理number与number+1的次数问题，注意结果可能超过int表示范围，需用long long存储

按记忆打的，不一定对

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
int main() {
  int n;
  while (cin >> n) {
    map<int, ll> ma;  // 数字-出现次数
    for (int i = 0; i < n; i++) {
      int x;
      cin >> x;
      ma[x]++;
    }
    ll ans = 0;
    for (auto& [number, times] : ma) {
      if (ma.count(number + 1) > 0) {  // 考虑number-number+1的组合
        ll another_times = ma[number + 1];
        if (times > 1) {  // 选择两个number 一个number+1
          ans += times * (times - 1) / 2 * another_times;
        }
        if (another_times > 1) {  // 选择两个number+1 一个number
          ans += another_times * (another_times - 1) / 2 * times;
        }
      }
    }
    cout << ans << endl;
  }
}

第三题

思路
由于是第三题，所以我默认它很难，我就直接使用暴力回溯写了一遍

数组排序
dfs:
	0: 达到终止条件，计算极差
	1: 将数组首部数据乘2
	2: dfs
	3: 还原数组
	4: 将数组尾部数据除2
	5: dfs
	6: 还原数组

细想一下可以知道，这根本不需要dfs，只需要for循环即可，不过我养成了思维定式，第三题一律暴力回溯

前面i个数据乘2，后面k-i个数据除2
for(int i=0;i<=k;i++){
	for(int j=0;j<i;j++){
		首部数据乘2
	}
	for(int j=0;j<k-i;j++){
		尾部数据除2
	}
}

另外我使用全排列写了一遍，不再使用以上的策略，直接所有情况枚举一遍

for(int i=start;i<vec.size();i++){
	swap(vec[i],vec[start];
	当前数字乘2
	dfs
	还原数字
	当前数字除2
	dfs
	还原数字
	swap(vec[i],vec[start];
}

最终我的解法都以超时结束，不知道用for循环实现可以得多少分

2023-3-16 蚂蚁机试

题目链接：「技术笔试」蚂蚁金服 2023-03-16
最终得分2.3分，第三题写了40分钟只得了30分，一直没找到bug

第一题 整数抽取

1e14 范围以内的一个正整数，将其每一数位上的奇数和偶数分别抽取出来组成两个新的数字，求这两差的绝对值。
思路
先将数字压入栈，然后计算奇数 偶数大小，上面的题解使用的是字符串存储数字，省去了压栈这一步

#include <bits/stdc++.h>
using namespace std;

using ll = long long;

ll GetValue(stack<int>& s) {  // 计算数字大小
  ll ans = 0;
  while (!s.empty()) {
    ans = ans * 10 + s.top();
    s.pop();
  }
  return ans;
}
int main() {
  ll n;
  while (cin >> n) {
    stack<int> one, two;
    while (n != 0) {
      int num = n % 10;
      if (num % 2 == 0) {  // 偶数
        two.emplace(num);
      } else if (num % 2 == 1) {  // 奇数
        one.emplace(num);
      }
      n /= 10;
    }
    cout << abs(GetValue(one) - GetValue(two)) << endl;
  }
}

第二题 组装电脑

n 组零件，每组零件有若干种，每一种有一个价格和性能。你需要从每组里面选出一种零件，使得总价格不超过 x，并且性能总和最大。
n <= 40, 所有零件的种类数不超过 40，其他数值 1e9。
思路
首先简单判断一下是否能完成组装，不能就直接返回，能的话就使用dfs穷举所有可能，找到最大性能

#include <bits/stdc++.h>
using namespace std;

using ll = long long;  // 全部使用long long存储，避免溢出
const ll kInf = 1 << 30;
void dfs(const vector<vector<pair<ll, ll>>>& vec, ll cur_index, ll cur_x, ll cur_v, ll& max_v) {
  if (cur_index >= vec.size()) {  // 选完所有零件，计算最大性能
    max_v = max(max_v, cur_v);
    return;
  }
  for (auto [a, v] : vec[cur_index]) {
    if (cur_x >= a) {  // 选择可选的零件
      dfs(vec, cur_index + 1, cur_x - a, cur_v + v, max_v);
    }
  }
}
int main() {
  ll n, x;
  while (cin >> n >> x) {
    vector<vector<pair<ll, ll>>> arr(n);
    ll min_x = 0;  // 最小零件价格总和
    for (ll i = 0; i < n; i++) {
      ll m, a, v;
      ll min_a = kInf;
      cin >> m;
      arr[i] = vector<pair<ll, ll>>(m);
      for (ll j = 0; j < m; j++) {
        cin >> arr[i][j].first;
        min_a = min(min_a, arr[i][j].first);  // 记录该类型零件最小价格
      }
      for (ll j = 0; j < m; j++) {
        cin >> arr[i][j].second;
      }
      min_x += min_a;
    }
    if (x < min_x) {  // 无法完成组装
      cout << -1 << endl;
      continue;
    }
    ll ans = 0;
    dfs(arr, 0, x, 0, ans);  // 计算最大零件价值和
    cout << ans << endl;
  }
}

第三题 带传送阵的矩阵游离

n 行 m 列的矩阵，每个位置上有一个元素。你可以上下左右行走，代价是前后两个位置元素值差的绝对值。另外，你最多可以使用一次传送阵（只能从一个数跳到另外一个相同的树），求从走上角走到右下角最少需要多少时间。
1 <= n, m <= 500, 1 <= aij <= 1e9。

思路
刚开始想了想，如果用dfs，应该能得30-60分，但当时时间也挺多的，就想完全通过。方法就是计算各点到起点的距离，计算各点到终点的距离，设使用传送阵的起始点为x，终点为y，最终的路径长度即为dist_form_start[x] + 0（传送阵代价） + dist_to_end[y]，可惜代码有bug，只得了30分，我觉得我思路是没问题的

以下为有bug的版本，先计算两个最短距离，然后使用传送计算最终距离

额，好像优先队列没设置为小顶堆，有点尴尬，这样都能得30分，运气不错
设置方式为

// 自带的比较函数
priority_queue<TP, vector<TP>, greater<TP>> q;
// 自定义比较函数
auto cmp = [](const pair<int, int>& p1, const pair<int, int>& p2) -> bool { return p1.second > p2.second; };
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(cmp)> qu(cmp);

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
const ll kInf = 0xfffffffffffff;
int main() {
  ll n, m;
  while (cin >> n >> m) {
    vector<vector<ll>> arr(n, vector<ll>(m));
    unordered_map<ll, vector<pair<ll, ll>>> ma;
    for (ll i = 0; i < n; i++) {
      for (ll j = 0; j < m; j++) {
        cin >> arr[i][j];
      }
    }

    for (ll i = 0; i < n; i++) {
      for (ll j = 0; j < m; j++) {
        if (ma.count(arr[i][j]) == 0) {
          vector<pair<ll, ll>> tmp;
          tmp.emplace_back(i, j);
          ma[arr[i][j]] = tmp;
        } else {
          ma[arr[i][j]].emplace_back(i, j);
        }
      }
    }
    vector<vector<ll>> dist1(n, vector<ll>(m, kInf));
    vector<vector<bool>> visit1(n, vector<bool>(m, false));
    priority_queue<tuple<ll, ll, ll>> qu;
    dist1[0][0] = 0;
    qu.emplace(0, 0, 0);
    while (!qu.empty()) {
      auto [from_start, i, j] = qu.top();
      qu.pop();
      if (visit1[i][j]) {
        continue;
      }
      visit1[i][j] = true;

      if (i + 1 < n) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i + 1][j]);
        if (dist1[i + 1][j] > cur_dist) {
          dist1[i + 1][j] = cur_dist;
          qu.emplace(cur_dist, i + 1, j);
        }
      }
      if (i - 1 >= 0) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i - 1][j]);
        if (dist1[i - 1][j] > cur_dist) {
          dist1[i - 1][j] = cur_dist;
          qu.emplace(cur_dist, i - 1, j);
        }
      }
      if (j + 1 < m) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i][j + 1]);
        if (dist1[i][j + 1] > cur_dist) {
          dist1[i][j + 1] = cur_dist;
          qu.emplace(cur_dist, i, j + 1);
        }
      }
      if (j - 1 >= 0) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i][j - 1]);
        if (dist1[i][j - 1] > cur_dist) {
          dist1[i][j - 1] = cur_dist;
          qu.emplace(cur_dist, i, j - 1);
        }
      }
    }
    vector<vector<ll>> dist2(n, vector<ll>(m, kInf));
    vector<vector<bool>> visit2(n, vector<bool>(m, false));
    dist2[n - 1][m - 1] = 0;
    qu.emplace(0, n - 1, m - 1);
    while (!qu.empty()) {
      auto [from_start, i, j] = qu.top();
      qu.pop();
      if (visit2[i][j]) {
        continue;
      }
      visit2[i][j] = true;

      if (i + 1 < n) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i + 1][j]);
        if (dist2[i + 1][j] > cur_dist) {
          dist2[i + 1][j] = cur_dist;
          qu.emplace(cur_dist, i + 1, j);
        }
      }
      if (i - 1 >= 0) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i - 1][j]);
        if (dist2[i - 1][j] > cur_dist) {
          dist2[i - 1][j] = cur_dist;
          qu.emplace(cur_dist, i - 1, j);
        }
      }
      if (j + 1 < m) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i][j + 1]);
        if (dist2[i][j + 1] > cur_dist) {
          dist2[i][j + 1] = cur_dist;
          qu.emplace(cur_dist, i, j + 1);
        }
      }
      if (j - 1 >= 0) {
        ll cur_dist = from_start + abs(arr[i][j] - arr[i][j - 1]);
        if (dist2[i][j - 1] > cur_dist) {
          dist2[i][j - 1] = cur_dist;
          qu.emplace(cur_dist, i, j - 1);
        }
      }
    }
    vector<vector<ll>> dist(n, vector<ll>(m, kInf));
    ll min_dist = kInf;
    for (ll i = 0; i < n; i++) {
      for (ll j = 0; j < m; j++) {
        auto vec = ma[arr[i][j]];
        for (auto [xi, xj] : vec) {
          if (dist1[i][j] != kInf && dist2[xi][xj] != kInf) {
            dist[i][j] = min(dist[i][j], dist1[i][j] + dist2[xi][xj]);
          }
        }
        min_dist = min(min_dist, dist[i][j]);
      }
    }
    cout << min_dist << endl;
  }
}

相比之下，牛客网上的题解就简洁多了，多加一个维度k，对维度同样使用状态转移，更加通用的做法，并且在处理方向上，我还是用习惯的方法，对每个方向进行枚举，而题解中则使用dir数组进行统一处理，既方便又不容易出错，map赋值时我还对是否存在该值进行分类讨论，实际上是不需要的，如果不存在map会先设置默认值而后进行更新

for (int i = 0; i < 4; i++) {
    int nx = x + dir[i][0], ny = y + dir[i][1];
    if (nx < 0 || nx >= n || ny < 0 || ny >= m || v[nx][ny][z] == 1) continue;
    if (d[nx][ny][z] > dist + abs(a[x][y] - a[nx][ny])) {
        d[nx][ny][z] = dist + abs(a[x][y] - a[nx][ny]);
        q.push({d[nx][ny][z], nx, ny, z});
    }
}

2023-03-19 米哈游机试

题目链接：全网首发-真题分享|3月19日米哈游校招研发岗三道题
参考题解：
米哈游笔试题目思路（客户端卷）
米哈游后端笔试题解

第一题

米小游拿到了一个矩阵，矩阵上有一格有一个颜色，为红色( R )。绿色( G )和蓝色( B )这三种颜色的一种。然而米小游是蓝绿色盲，她无法分游蓝色和绿色，所以在米小游眼里看来，这个矩阵只有两种颜色，因为蓝色和绿色在她眼里是一种颜色。米小游会把相同颜色的部分看成是一个连通块。请注意，这里的连通划是上下左右四连通的。由于色盲的原因，米小游自己看到的连通块数量可能比真实的连通块数量少。你可以帮米小游计算连通块少了多少吗？

思路
看到连通分量，就自然而然想用并查集实现，实际上只需要连接两个方向的节点

#include <bits/stdc++.h>
using namespace std;

class UnionFind {  // 并查集类
 public:
  UnionFind(int size) {  // 初始化
    data_ = vector<int>(size);
    for (int i = 0; i < size; i++) {
      data_[i] = i;
    }
  }

  int Find(int k) {  // 查找
    if (data_[k] == k) {
      return k;
    }
    data_[k] = Find(data_[k]);
    return data_[k];
  }
  void Union(int p, int q) {  // 合并
    int rootp = Find(p);
    int rootq = Find(q);
    data_[rootp] = rootq;
  }
  int Size() {  // 连通分量数目
    int size = 0;
    for (int i = 0; i < data_.size(); i++) {
      if (data_[i] == i) {
        size++;
      }
    }
    return size;
  }

 private:
  vector<int> data_;
};

int main() {
  int n, m;
  int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
  while (cin >> n >> m) {
    vector<vector<char>> arr(n, vector<char>(m));
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        cin >> arr[i][j];
      }
    }
    // 真实情况连通数量
    UnionFind uf1(n * m);
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        for (int k = 0; k < 4; k++) {
          int nx = i + dir[k][0];
          int ny = j + dir[k][1];
          if (nx >= 0 && nx < n && ny >= 0 && ny < m && arr[i][j] == arr[nx][ny]) {
            uf1.Union(i * m + j, nx * m + ny);
          }
        }
      }
    }
    int size1 = uf1.Size();
    // 视角连通分量数量
    UnionFind uf2(n * m);
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        for (int k = 0; k < 4; k++) {
          int nx = i + dir[k][0];
          int ny = j + dir[k][1];
          if (nx >= 0 && nx < n && ny >= 0 && ny < m && ((arr[i][j] == 'R') == (arr[nx][ny] == 'R'))) {
            uf2.Union(i * m + j, nx * m + ny);
          }
        }
      }
    }
    int size2 = uf2.Size();
    cout << size1 - size2 << endl;
  }
}

dfs的解法如下，比并查集少一点代码，写起来快点

#include <bits/stdc++.h>
using namespace std;
void dfs(vector<vector<char>>& vec, vector<vector<bool>>& visit, int x, int y, char target, int n, int m) {
  visit[x][y] = true;  // 设置成已访问
  static int dir[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
  for (int k = 0; k < 4; k++) {  // 遍历四个方向
    int nx = x + dir[k][0];
    int ny = y + dir[k][1];
    if (nx >= 0 && nx < n && ny >= 0 && ny < m && visit[nx][ny] == false && vec[nx][ny] == target) {  // 坐标合法，未访问过，为目标值
      dfs(vec, visit, nx, ny, target, n, m);
    }
  }
}
int main() {
  int n, m;
  while (cin >> n >> m) {
    vector<vector<char>> arr(n, vector<char>(m));
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        cin >> arr[i][j];
      }
    }
    vector<vector<bool>> visit1(n, vector<bool>(m, false));
    int cnt1 = 0;  // 连通分量数目
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (visit1[i][j] == false) {
          cnt1++;
          dfs(arr, visit1, i, j, arr[i][j], n, m);
        }
      }
    }
    // 将蓝色改成绿色
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (arr[i][j] == 'B') {
          arr[i][j] = 'G';
        }
      }
    }
    vector<vector<bool>> visit2(n, vector<bool>(m, false));
    int cnt2 = 0;  // 连通分量数目
    for (int i = 0; i < n; i++) {
      for (int j = 0; j < m; j++) {
        if (visit2[i][j] == false) {
          cnt2++;
          dfs(arr, visit2, i, j, arr[i][j], n, m);
        }
      }
    }
    cout << cnt1 << " " << cnt2 << endl;
    cout << cnt1 - cnt2 << endl;
  }
}

第二题

米小游拿到了一个字符串 s 。她可以进行任意次以下两种操作：
1 删除 s 的一个 “mhy” 子序列。
2 添加一个 “mhy” 子序列在 s 上。
例如，给定 s 为 “mhbdy” ，米小游进行一次操作后可以使 s 变成 “bd” ，或者变成 “mhmbhdyy” 。
米小游想知道，经过若干次操作后 s 是否可以变成 t ？
注：子序列在原串中的顺序也是从左到右，但可以不连续。

思路
觉得写不出来，就直接进行骗分策略，看了别人的题解才发现解法很简单，最重要的是想到mhy三个字母的序列不重要

#include <bits/stdc++.h>
using namespace std;

bool Check(string& s, string& t) {
  vector<int> num1(26, 0);
  vector<int> num2(26, 0);
  // 统计字符串各字母次数
  for (char c : s) {
    num1[c - 'a']++;
  }
  for (char c : t) {
    num2[c - 'a']++;
  }
  int m, h, y;  // 记录mhy字母次数差值
  for (int i = 0; i < 26; i++) {
    if (i == 'm' - 'a') {
      m = num1[i] - num2[i];
    } else if (i == 'h' - 'a') {
      h = num1[i] - num2[i];
    } else if (i == 'y' - 'a') {
      y = num1[i] - num2[i];
    } else if (num1[i] != num2[i]) {  // 其他字母数量不相等，不能转换
      return false;
    }
  }
  return (m == h) && (h == y);  // 差值相等则可以进行转换
}
int main() {
  int q;
  cin >> q;
  for (int i = 0; i < q; i++) {
    string s, t;
    cin >> s >> t;
    if (Check(s, t)) {
      cout << "Yes" << endl;
    } else {
      cout << "No" << endl;
    }
  }
}

第三题

思路：
我的思路与题解一样，只不过我少了倍数预处理的一步，直接两层for循环找到因数更新dp数组

#include <bits/stdc++.h>
using namespace std;

using ll = long long;
const int mod = 1e9 + 7;
const int kMax = 1e6 + 1;
vector<bool> visit(kMax, false);   // visit[i]: 数字i是否出现
vector<vector<int>> factor(kMax);  // factor[i]: i的各个因数
vector<ll> dp(kMax, 0);            // dp[i]: 以i结尾的数字集合数目
int main() {
  int n;
  cin >> n;
  vector<int> a(n);
  for (int i = 0; i < n; i++) {
    cin >> a[i];
    visit[a[i]] = true;
  }
  sort(a.begin(), a.end());  // 数字排序
  int max_n = a[n - 1];      // 最大数字
  // 预处理倍数关系
  for (int i = 1; i <= max_n; i++) {
    if (visit[i] == false) {
      continue;
    }
    for (int j = i + i; j <= max_n; j += i) {
      if (visit[j] == true) {
        factor[j].emplace_back(i);  // i为j的因数
      }
    }
  }
  for (int i = 1; i < n; i++) {
    for (int num : factor[a[i]]) {
      dp[a[i]] += dp[num] + 1;  // a[i]可以和num的数字集合全部组合一遍，最后加上{num,a[i]}
    }
    dp[a[i]] %= mod;
  }
  ll ans = 0;
  for (int i = 1; i < n; i++) {
    ans += dp[a[i]];
  }
  ans %= mod;
  cout << ans << endl;
}

2023-03-23 腾讯音乐笔试

题目：3.23 腾讯音乐 暑期 实习 技术类 笔试
中途肚子痛，提前半小时交卷了，第一题写了一半，第二题dfs骗了几十分，第三题签到

笔试或面试前千万别吃坏肚子

第一题

这个问题可以分解成两个子问题：
1 通过层序遍历得到奇偶层节点个数
2 假设奇数层节点个数为k，解决是否能从[1,n]中选择k个数，总和为target问题

若1-n总和为偶数，则target为sum/2，若为奇数，则target为sum/2或sum/2+1

代码片段如下：（不一定对）
第一步：层序遍历

  TreeNode* fun(TreeNode* root) {
    queue<Info> qu;
    int one = 0;                 // 奇数节点数
    int two = 0;                 // 偶数节点数
    stack<TreeNode*> one_stack;  // 奇数节点栈
    stack<TreeNode*> two_stack;  // 偶数节点栈
    qu.emplace(root, 1);
    while (!qu.empty()) {
      Info info = qu.front();
      TreeNode* node = info.first;
      int level = info.second;
      qu.pop();
      if (level % 2 == 1) {
        one++;
        one_stack.emplace(node);
      } else {
        two++;
        two_stack.emplace(node);
      }
      if (node->left != nullptr) {  // 将左子树节点压入队列
        qu.emplace(node->left, level + 1);
      }
      if (node->right != nullptr) {  // 将右子树节点压入队列
        qu.emplace(node->right, level + 1);
      }
    }
  }

第二步：选择k个数总和为target
双指针法求得可能结果

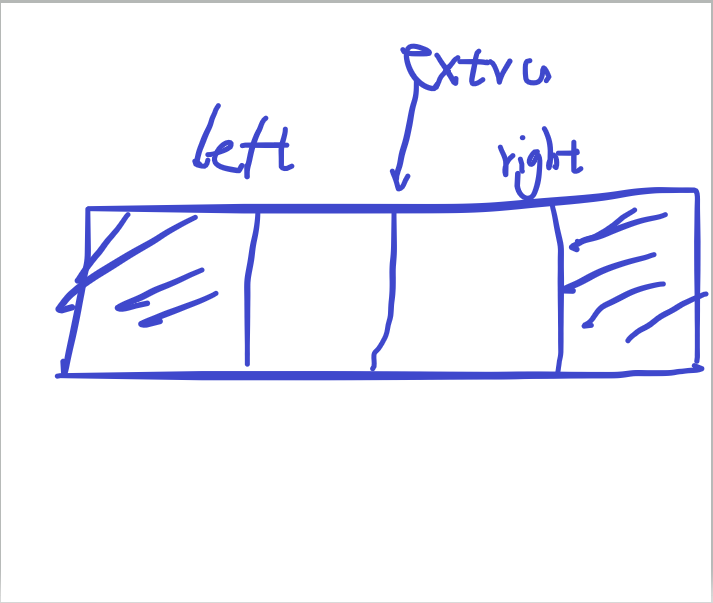
刚开始左区域最大，右区域为空，此时sum最小，而后一直将left right向左移动，增大sum，直至sum>target

#include <bits/stdc++.h>
using namespace std;

vector<int> FindSuitNumber(int n, int k, int target) {  // [1,n]中选择k个数，总和为target
  // 等差数列求和公式：Sn = n * (a1 + an) / 2
  int min_sum = k * (1 + k) / 2;
  int max_sum = k * (n - k + 1 + n) / 2;
  if (target < min_sum || target > max_sum) {
    // printf("target %d: no suit number\n", target);
    return {};
  }
  // 如果target属于[min_sum,max_sum]，则target一定能取到
  vector<int> seq(n);
  for (int i = 0; i < n; i++) {
    seq[i] = i + 1;
  }
  // 最后数据构成：0...left  extra_num right+1...n-1
  int left = k - 1;
  int right = n - 1;
  int sum = min_sum;
  int extra_num = -1;
  while (left >= 0) {
    int sub = seq[right] - seq[left];
    if (sum + sub < target) {  // 小于目标值，将右侧元素加入集合
      left--;
      right--;
      sum += sub;
    } else {
      extra_num = seq[left] + target - sum;
      left--;
      break;
    }
  }

  vector<int> ans;
  for (int i = 0; i <= left; i++) {
    ans.emplace_back(seq[i]);
  }

  ans.emplace_back(extra_num);

  for (int i = right + 1; i < n; i++) {
    ans.emplace_back(seq[i]);
  }
  // 校验结果
  int result = accumulate(ans.begin(), ans.end(), 0);
  if (result != target) {  // 总和不为target
    printf("target: %d result: %d\n", target, result);
  }
  if (ans.size() != k) {  // 数量错误
    printf("wrong ans size: %d", ans.size());
  }
  set<int> se;
  for (int num : ans) {
    if (num < 1 || num > n) {  // 数字超出范围
      printf("wrong value: %d\n", num);
    }
    if (se.count(num) > 0) {  // 重复数字
      printf("repeat value: %d\n", num);
    }
    se.emplace(num);
  }

  return ans;
}

int main() {
  for (int i = 0; i < 10000; i++) {
    for (int j = 1; j <= 100; j++) {
      FindSuitNumber(100, j, i);
    }
  }
}

第二题

算法实现中为避免函数参数过多，可以将公有的数据结构放在类成员中，且没必要遵循命名规范（类成员名后加_），类成员的设置应该在具体实现前想好。

第二题看别人说是最大值最小化问题，使用二分+贪心的方法解决，但没看到啥具体实现
（二分答案，贪心验证答案是否符合，符合就再缩小一点答案，不符合就扩大一点 ）

#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  int getValue(int start, int end) {  // 计算str[str,end)的metric，种类x长度
    vector<int> num(26, 0);           // 字符出现次数
    for (int i = 0; i < 26; i++) {
      num[i] = char_num_[end][i] - char_num_[start][i];
    }
    int diff = 0;  // 不同字符数目
    for (int i = 0; i < 26; i++) {
      if (num[i] > 0) {
        diff++;
      }
    }
    return diff * (end - start);
  }
  int computeMaxValue() {
    int max_value = 0;  // 计算最大metric
    // 分割位置集合[0,seq0,seq1,..seqk-1,length]
    for (int i = 0; i < k_; i++) {
      if (i == k_ - 1) {
        max_value = max(max_value, getValue(seq_[i], length_));  // 最后一个切割位置，与数组末尾配对
      } else {
        max_value = max(max_value, getValue(seq_[i], seq_[i + 1]));
      }
    }
    return max_value;
  }
  void dfs(int index, int& max_value) {
    if (index == k_) {
      max_value = min(max_value, computeMaxValue());  // 记录最小的最大metric
      return;
    }
    for (int i = index; i < seq_.size(); i++) {  // 全排列，但seq[i]>seq[i-1]
      if (seq_[i] > seq_[index - 1]) {
        swap(seq_[index], seq_[i]);
        dfs(index + 1, max_value);
        swap(seq_[index], seq_[i]);
      }
    }
  }
  int getMaxValue(string str, int k) {
    k_ = k;
    length_ = str.length();
    char_num_ = vector<vector<int>>(str.length() + 1, vector<int>(26, 0));  // char_num_[i]表示s[i]前的各字符出现次数，用于快速计算区间字符种类
    for (int i = 0; i < str.length(); i++) {
      char_num_[i + 1] = char_num_[i];
      char_num_[i + 1][str[i] - 'a']++;
    }

    if (k == 1) {
      return getValue(0, str.length());  // 不需要分割，直接计算metric
    }
    seq_ = vector<int>(str.length());
    for (int i = 0; i < str.length(); i++) {
      seq_[i] = i;
    }
    int ans = 1 << 30;
    dfs(1, ans);  // 第一位一定为0，数组开始索引为1
    return ans;
  }

 private:
  vector<vector<int>> char_num_;
  vector<int> seq_;
  int k_;
  int length_;
};
int main() {
  Solution solution;
  solution.getMaxValue("ababbbb", 2);
}

第三题

签到题

#include <bits/stdc++.h>
using namespace std;
class Solution {
 public:
  int getCnt(string str) {
    int ans = 0;
    for (int i = 0; i < str.length() - 1; i++) {
      int sub = abs(str[i] - str[i + 1]);
      if (sub == 'a' - 'A' || sub == 0) {
        ans++;
      }
    }
    return ans;
  }
};

2023-03-26 腾讯笔试

题目：腾讯笔试记录0326（研发）
就写出了第一第二题，第三题题目有点问题，导致我写了40分钟没得啥分，一直没理解最后一个样例是怎么来的，第四第五题一看就是我不会的题目，随便写了写

第一题 链表操作

链表中相邻节点两两一组，然后相邻两组之间进行交换
类似的题目：25. K 个一组翻转链表
直接将链表节点指针存入数组，便于理解

class Solution {
 public:
  ListNode* reorderList(ListNode* head) {
    ListNode virt_head(-1);  // 虚拟头节点
    virt_head.next = head;
    vector<ListNode*> arr;
    ListNode* cur = head;
    while (cur != nullptr) {
      arr.emplace_back(cur);
      cur = cur->next;
    }
    int num = arr.size();
    ListNode* prev = &virt_head;  // 待处理组的前一个节点
    for (int i = 0; i + 3 < num; i += 4) {
      prev->next = arr[i + 2];              // 指向第二组的头节点
      arr[i + 1]->next = arr[i + 3]->next;  // 指向第二组后一个节点
      prev = arr[i + 1];                    // 更新prev节点
      arr[i + 3]->next = arr[i];            // 更新第二组的next为第一组头节点
    }
    if (num % 4 == 3) {  // 剩下3个节点，特殊处理
      prev->next = arr[num - 1];
      arr[num - 2]->next = arr[num - 1]->next;
      arr[num - 1]->next = arr[num - 3];
    }
    return virt_head.next;
  }
};

第二题 重组字符串

给定N个字符串，每个字符串全部由小写字母组成，且每个字符串的长度最多为8,请你断有多少重组字符串，重组字符串有以下规则：1.从每个字符串里面都抽取1个字母组成。2.新字符串不能有2个相同的字母。请问总共能组成多少个重组字符串。

字符串长度比较小，用dfs暴力枚举即可

#include <bits/stdc++.h>
using namespace std;
void dfs(vector<string>& strs, int index, string cur_str, set<string>& res) {
  if (index == strs.size()) {  // 加入结果集合
    res.emplace(cur_str);
    return;
  }
  for (char c : strs[index]) {
    if (cur_str.find(c) == string::npos) {  // 无重复字母
      cur_str.push_back(c);                 // 加入字符串
      dfs(strs, index + 1, cur_str, res);   // 遍历下一个字符串
      cur_str.pop_back();                   // 还原
    }
  }
}
int main() {
  int n;
  cin >> n;
  vector<string> strs(n);
  for (int i = 0; i < n; i++) {
    cin >> strs[i];
  }
  set<string> ans;  // 使用set去重
  dfs(strs, 0, "", ans);
  cout << ans.size();
}

第三题 最小权值排列数组

给定2个整数数组A,B,数组长度都为N,数组B为权值数组，权值数据范国为[0,2],请你构造一个数组C,满足以下条件：
1,长应为N
2.数组元素范国为[1,N],且元素值不能更复，即为N的一个排列
3.如果数组下标i<j，且有B[i]>B[j],那么一定要保证C[i]>C[j]
4数组C与数组A每个元素之差的和的绝对值最小.

按理来说样例的答案应该是98，但样例是104，一直想不出来为什么

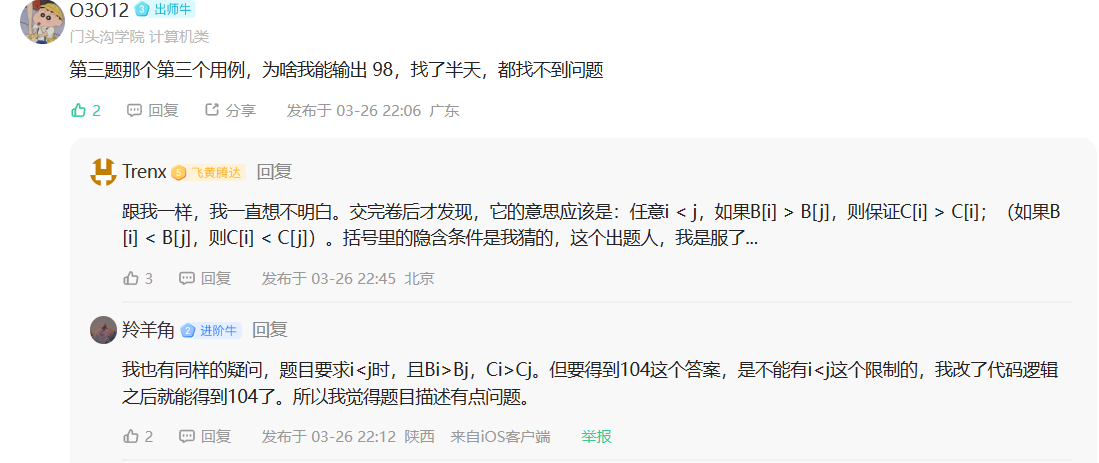
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int kMax = 2 * 10e5 + 1;
vector<int> A(kMax);
vector<int> B(kMax);
int n;
ll ans = 0xffffffffffff;
void dfs(vector<ll>& seq, int index, int one_min, int two_min) {  // one_min 前面1位置的最小值 two_min 前面2位置的最小值
  if (index == n) {
    ll array_abs_sum = 0;  // 差值的绝对值之和
    for (int i = 0; i < n; i++) {
      array_abs_sum += abs(seq[i] - A[i]);
    }
    ans = min(ans, array_abs_sum);
    // 打印样例序列
    if (array_abs_sum == 98) {
      for (int num : seq) {
        cout << num << " ";
      }
      cout << endl;
    }
    return;
  }

  for (int i = index; i < n; i++) {
    if (B[index] == 0) {
      if (seq[i] < one_min && seq[i] < two_min) {  // 需小于1最小值与2最小值
        swap(seq[i], seq[index]);
        dfs(seq, index + 1, one_min, two_min);
        swap(seq[i], seq[index]);
      }
    } else if (B[index] == 1) {
      if (seq[i] < two_min) {  // 需小于2最小值
        int new_one_min = min<ll>(seq[i], one_min);
        swap(seq[i], seq[index]);
        dfs(seq, index + 1, new_one_min, two_min);  // 更新1最小值
        swap(seq[i], seq[index]);
      }
    } else {
      int new_two_min = min<ll>(seq[i], two_min);
      swap(seq[i], seq[index]);
      dfs(seq, index + 1, one_min, new_two_min);  // 更新2最小值
      swap(seq[i], seq[index]);
    }
  }
}
int main() {
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> A[i];
  }
  for (int i = 0; i < n; i++) {
    cin >> B[i];
  }
  vector<ll> seq(n);  // [1,n]序列
  for (int i = 0; i < n; i++) {
    seq[i] = i + 1;
  }
  dfs(seq, 0, kMax + 1, kMax + 1);
  cout << ans << endl;
}

/*
6
100 2 3 1 5 6
0 1 2 0 2 1
样例答案：104
我的答案：98
6 2 4 1 5 3
98
*/

2023-03-28 百度笔试

题目链接：3.28百度笔试复盘

图解SQL的inner join、left /right join、 outer join区别

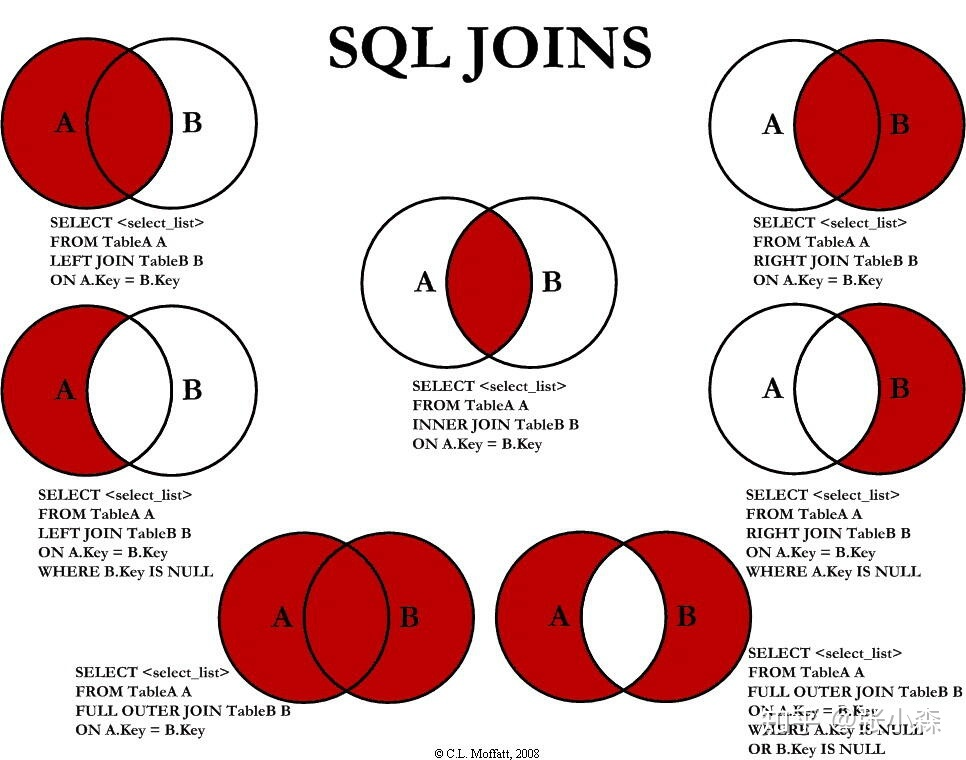
编程题过了2.8道，第三题一直超时，只得了80分

第一题

题目：

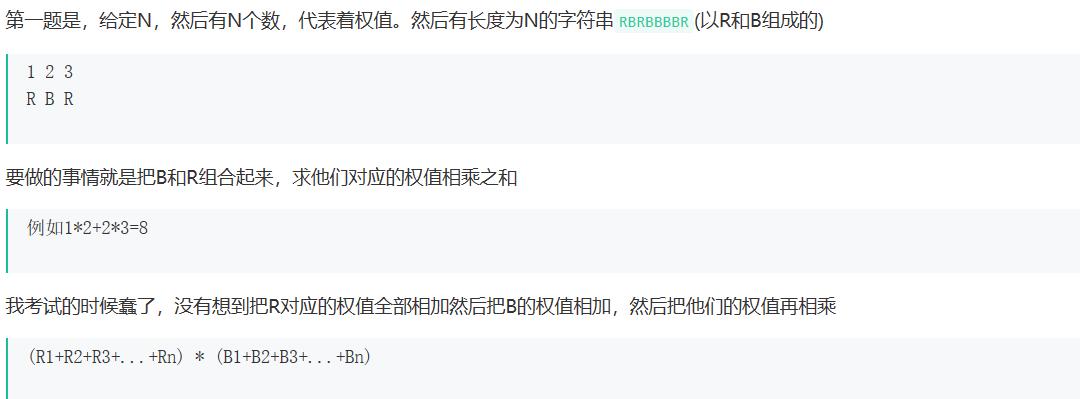
签到题

#include <bits/stdc++.h>
using namespace std;

const int kMod = 1e9 + 7;
using ll = long long;
int main() {
  int n;
  cin >> n;
  vector<int> a(n);
  for (int i = 0; i < n; i++) {
    cin >> a[i];
  }
  string str;
  cin >> str;
  ll red_sum = 0;   // 红色权值之和
  ll blue_sum = 0;  // 蓝色权值之和
  for (int i = 0; i < n; i++) {
    if (str[i] == 'R') {
      red_sum = (red_sum + a[i]) % kMod;
    } else {
      blue_sum = (blue_sum + a[i]) % kMod;
    }
  }
  ll ans = (red_sum * blue_sum) % kMod;
  cout << ans << endl;
}

第二题

题目：

标准解法是单调栈，不过我当时没想到，就用数组存从当前位置往右看最大value的索引

#include <bits/stdc++.h>
using namespace std;

int main() {
  string str;
  cin >> str;
  int length = str.length();
  string ans = "0.";
  vector<int> max_see(length);  // 从当前位置往右看最大value的索引
  max_see[length - 1] = length - 1;
  for (int i = length - 2; i >= 2; i--) {
    char next_max_value = str[max_see[i + 1]];
    if (str[i] >= next_max_value) {  // 当前位置比右边最大值大
      max_see[i] = i;
    } else {  // 当前位置比右边最大值小
      max_see[i] = max_see[i + 1];
    }
  }
  for (int i = 2; i < length; i++) {
    ans.push_back(str[max_see[i]]);
    i = max_see[i];
  }
  cout << ans << endl;
}

第三题

题目：

只得了80分，要么时间超时，要么内存使用过多，可以优化的点在于输入x y时将信息暂存到某一个地方，而后在树遍历的过程中一次性计算所有，而不是每次都遍历x的所有子节点，并与info相加，不过最后没时间了，就没实现

#include <bits/stdc++.h>
using namespace std;
using NumberInfo = pair<int, int>;  // 记录数字中2，5因数的个数
NumberInfo GetInfo(int x) {         // 得到数字2，5因数的个数
  int two = 0, five = 0;
  while (x > 0 && x % 2 == 0) {
    two++;
    x = x / 2;
  }
  while (x > 0 && x % 5 == 0) {
    five++;
    x = x / 5;
  }
  return {two, five};
}

void AddInfo(NumberInfo& p1, NumberInfo p2) {  // 因数个数相加
  p1.first += p2.first;
  p1.second += p2.second;
}

int main() {
  int n, q;
  cin >> n;
  vector<bool> visited(n + 1, false);  // 该节点是否出现
  vector<int> tree(n + 1);             // 使用数组维护树结构
  vector<vector<int>> child(n + 1);    // 节点的子节点（包括自身）
  vector<NumberInfo> num(n + 1);       // 各节点2,5因数个数
  for (int i = 1; i <= n; i++) {
    int a;
    cin >> a;
    num[i] = GetInfo(a);
    child[i].emplace_back(i);
  }
  // 构建树结构，1为根节点
  visited[1] = true;
  tree[1] = 1;
  for (int i = 0; i < n - 1; i++) {
    int u, v;
    cin >> u >> v;
    // 确定哪个为父节点
    if (visited[u]) {
      tree[v] = u;
      visited[v] = true;
    } else {
      tree[u] = v;
      visited[u] = true;
    }
  }
  visited.clear();
  // 计算各节点子节点信息
  for (int i = 2; i <= n; i++) {
    int root = i;
    do {
      root = tree[root];
      child[root].emplace_back(i);
    } while (root != 1);
  }
  cin >> q;
  for (int i = 0; i < q; i++) {
    int x, y;
    cin >> x >> y;
    NumberInfo info = GetInfo(y);
    // 所有子节点信息加上info因数个数
    for (auto node : child[x]) {
      AddInfo(num[node], info);
    }
  }
  // 计算各节点的最终值（因数2与因数5的个数）
  for (int i = 2; i <= n; i++) {
    int root = i;
    do {
      root = tree[root];
      AddInfo(num[root], num[i]);
    } while (root != 1);
  }
  // 计算各节点后缀0的个数（因数2与因数5个数的较小值）
  for (int i = 1; i <= n; i++) {
    cout << min(num[i].first, num[i].second) << " ";
  }
}

杂项

判断字符串

ali字符串，刚开始忽略了对开头字符是否为Aa的判断，只有3种状态

#include <bits/stdc++.h>
using namespace std;

int main() {
  string str;
  int n;
  cin >> n;
  for (int i = 0; i < n; i++) {
    cin >> str;
    int status = 0;      //  状态机转换  0：初始状态 1：遇到Aa 2：遇到lL 3: 遇到iI
    bool error = false;  // 是否发生错误
    for (char c : str) {
      if (status == 0) {
        if (c == 'a' || c == 'A') {  //  状态转换
          status = 1;
        } else {  // 预期之外的值，发生错误
          error = true;
          break;
        }
      } else if (status == 1) {
        if (c == 'l' || c == 'L') {  //  状态转换
          status = 2;
        } else if (c != 'a' && c != 'A') {  // 预期之外的值，发生错误
          error = true;
          break;
        }
      } else if (status == 2) {
        if (c == 'i' || c == 'I') {  //  状态转换
          status = 3;
        } else if (c != 'l' && c != 'L') {  // 预期之外的值，发生错误
          error = true;
          break;
        }
      } else if (status == 3) {
        if (c != 'i' && c != 'I') {  // 预期之外的值，发生错误
          error = true;
          break;
        }
      }
    }
    if (error || status != 3) {  // 发生错误或未遇到i
      cout << "No" << endl;
    } else {
      cout << "Yes" << endl;
    }
  }
}

01翻转

使用dfs遍历各个翻转可能，加上一点剪枝策略，骗分
正确思路

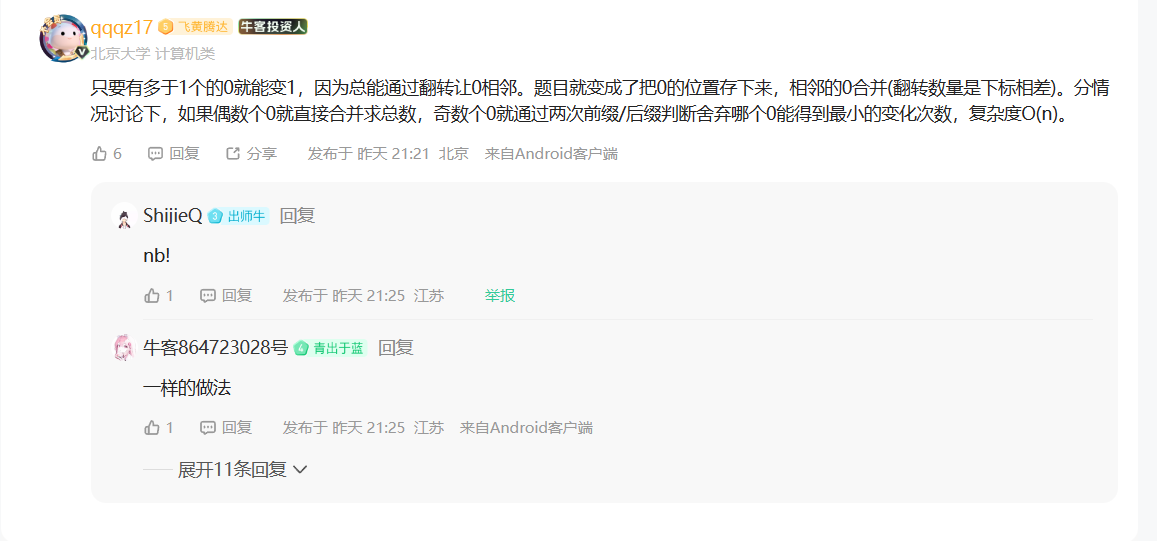
dfs优化思路

可以使用备忘录的方式减少各个点最大获得价值的重复计算

#include <bits/stdc++.h>
using namespace std;
const int kMax = 10001;
const int kInf = -1 * (1 << 30);
int n;
vector<int> food(kMax);
vector<vector<int>> path(kMax);
vector<int> max_get(kMax, kInf);

// void dfs(int cur_id, int cur_value, int& max_value) {
//   cur_value += food[cur_id];
//   max_value = max(max_value, cur_value);
//   for (int dst_id : path[cur_id]) {
//     dfs(dst_id, cur_value, max_value);
//   }
// }

int dfs(int cur_id, int cur_value) {
  cur_value += food[cur_id];
  int max_value = cur_value;
  for (int dst_id : path[cur_id]) {
    if (max_get[dst_id] == kInf) {
      max_get[dst_id] = dfs(dst_id, cur_value);
    }
    max_value = max(max_value, max_get[dst_id]);
  }
  return max_value;
}

int main() {
  cin >> n;
  for (int i = 0; i < n; i++) {
    int id, parent_id, value;
    cin >> id >> parent_id >> value;
    food[id] = value;
    if (parent_id != -1) {
      path[parent_id].emplace_back(id);
    }
  }
  int ans = 0;
  for (int id = 0; id < n; id++) {
    int tmp = dfs(id, 0);
    ans = max(ans, tmp);
  }
  cout << ans << endl;
}

/*
7
0 1 8
1 -1 -2
2 1 9
4 0 -2
5 4 3
3 0 -3
6 2 -3
*/