数据结构–最短路径 Dijkstra算法

Dijkstra算法
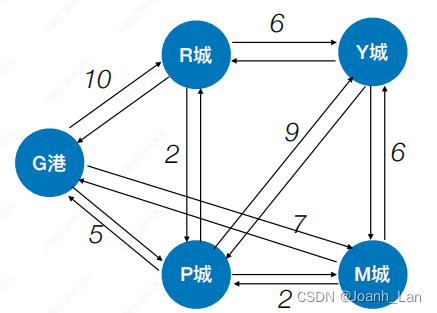
计算 b e g i n 点到各个点的最短路 \color{red}计算\ begin\ 点到各个点的最短路 计算 begin 点到各个点的最短路

如果是无向图,可以先把无向图转化成有向图

我们需要2个数组
final[] (标记各顶点是否已找到最短路径)与 dis[] (最短路径⻓度)数组
Dijkstra算法是一种用于寻找图中最短路径的算法,它的步骤如下:
- 初始化:将起始节点的最短路径设置为0,其他节点的最短路径设置为正无穷大。
- 选取最短路径最小的节点作为当前节点。
- 更新当前节点的邻居节点的最短路径:如果通过当前节点到达邻居节点的路径比邻居节点当前的最短路径更短,则更新邻居节点的最短路径。
- 标记当前节点为已访问(已经找到 b e g i n begin begin 到该点的最短路)。
- 重复步骤2 → \to → 4,直到所有节点都被访问过或者没有可达到的节点。
- 根据最短路径和前驱节点构建最短路径树或者路径数组。
以上就是Dijkstra算法的基本步骤。在实际应用中,可以使用优先队列来选取最短路径最小的节点,以提高算法的效率 (堆Dijkstra)。

V0到V2 的最短(带权)路径⻓度为:dist[2] = 9
通过 path[ ] 可知,V0到V2 的最短(带权)路径:
v
0
→
v
4
→
v
1
→
v
2
v_0 \to v_4 \to v_1 \to v_2
v0→v4→v1→v2
Dijkstra算法的时间复杂度
时间复杂度: O ( n 2 ) 即 O ( ∣ V ∣ 2 ) O(n^2)即O(|V|^2) O(n2)即O(∣V∣2)
代码实现
int g[N][N]; // 存储每条边
int dist[N]; // 存储1号点到每个点的最短距离
bool st[N]; // 存储每个点的最短路是否已经确定
//时间复杂是 O(n2+m), n 表示点数,m 表示边数
// 求1号点到n号点的最短路,如果不存在则返回-1
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
for (int i = 0; i < n - 1; i++)
{
int t = -1; // 在还未确定最短路的点中,寻找距离最⼩的点
for (int j = 1; j <= n; j++)
if (!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
// ⽤t更新其他点的距离
for (int j = 1; j <= n; j++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f)
return -1;
return dist[n];
}
负权值带权图问题,Dijkstra不可用
负权值带权图问题, D i j k s t r a 不可用!!! \color{red}负权值带权图问题,Dijkstra不可用!!! 负权值带权图问题,Dijkstra不可用!!!
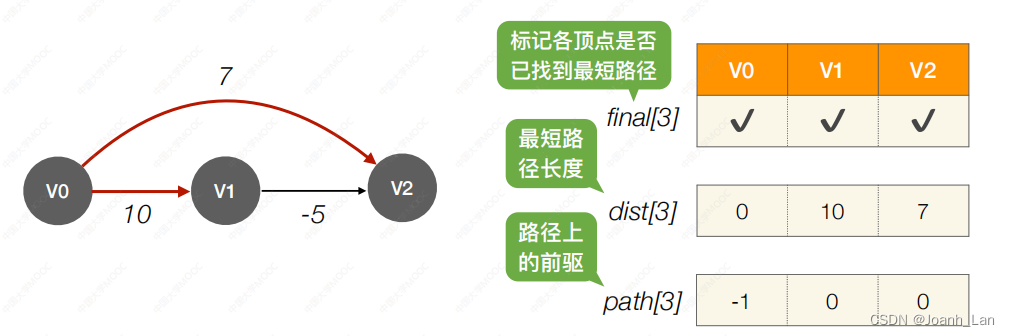
事实上
V
0
V_0
V0 到
V
2
V_2
V2 的最短带权路径⻓度为 5
结论:Dijkstra 算法不适⽤于有负权值的带权图