今日份题目：

给你一个由 n 个数对组成的数对数组 pairs ，其中 pairs[i] = [lefti, righti] 且 lefti < righti 。

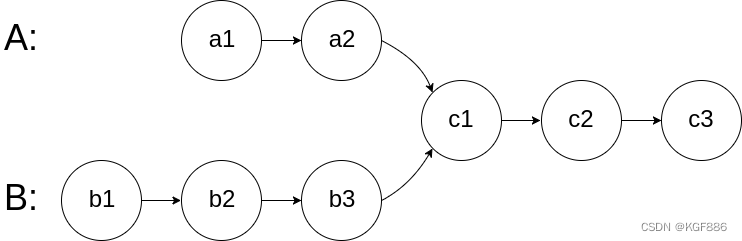
现在，我们定义一种 跟随 关系，当且仅当 b < c 时，数对 p2 = [c, d] 才可以跟在 p1 = [a, b] 后面。我们用这种形式来构造 数对链 。

找出并返回能够形成的 最长数对链的长度 。

你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

示例1

输入：pairs = [[1,2], [2,3], [3,4]]
输出：2
解释：最长的数对链是 [1,2] -> [3,4] 。

示例2

输入：pairs = [[1,2],[7,8],[4,5]]
输出：3
解释：最长的数对链是 [1,2] -> [4,5] -> [7,8] 。

提示

• n == pairs.length

• 1 <= n <= 1000

• -1000 <= lefti < righti <= 1000

题目思路

动态规划，一维dp数组记录到目前为止的最长数对链数值。

状态转移方程：

找到当前位置之前的满足递增的最长dp值的那一组，找不到就是自己（1）。

dp[i]=max(dp[i],dp[j]+1);

代码

class Solution 
{
public:
    int findLongestChain(vector<vector<int>>& pairs) 
    {
        int n=pairs.size();
        vector<int> dp(n,1);//记录到目前为止的最长数对链
        sort(pairs.begin(),pairs.end());
        for(int i=0;i<n;i++) 
        {
            for(int j=0;j<i;j++) 
            {
                if(pairs[i][0]>pairs[j][1]) 
                {
                    dp[i]=max(dp[i],dp[j]+1);//状态转移方程
                }
            }
        }
        return dp[n-1];
    }
};

提交结果

 欢迎大家在评论区讨论，如有不懂的代码部分，欢迎在评论区留言！