原题链接：

457. 环形数组是否存在循环

https://leetcode.cn/problems/circular-array-loop/description/

完成情况：

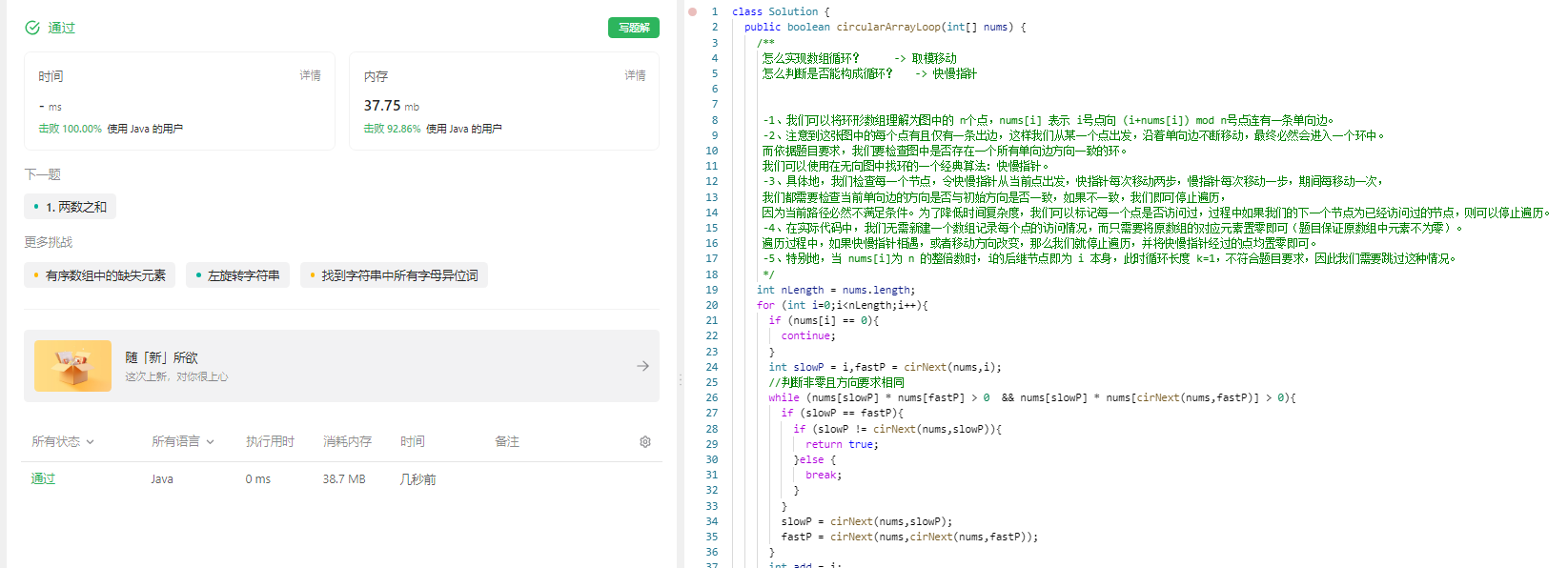
在这里插入图片描述

解题思路：

	/**
	 怎么实现数组循环？     -> 取模移动
	 怎么判断是否能构成循环？   -> 快慢指针


	 -1、我们可以将环形数组理解为图中的 n个点，nums[i] 表示 i号点向 (i+nums[i]) mod n号点连有一条单向边。
	 -2、注意到这张图中的每个点有且仅有一条出边，这样我们从某一个点出发，沿着单向边不断移动，最终必然会进入一个环中。
	 而依据题目要求，我们要检查图中是否存在一个所有单向边方向一致的环。
	 我们可以使用在无向图中找环的一个经典算法：快慢指针。
	 -3、具体地，我们检查每一个节点，令快慢指针从当前点出发，快指针每次移动两步，慢指针每次移动一步，期间每移动一次，
	 我们都需要检查当前单向边的方向是否与初始方向是否一致，如果不一致，我们即可停止遍历，
	 因为当前路径必然不满足条件。为了降低时间复杂度，我们可以标记每一个点是否访问过，过程中如果我们的下一个节点为已经访问过的节点，则可以停止遍历。
	 -4、在实际代码中，我们无需新建一个数组记录每个点的访问情况，而只需要将原数组的对应元素置零即可（题目保证原数组中元素不为零）。
	 遍历过程中，如果快慢指针相遇，或者移动方向改变，那么我们就停止遍历，并将快慢指针经过的点均置零即可。
	 -5、特别地，当 nums[i]为 n 的整倍数时，i的后继节点即为 i 本身，此时循环长度 k=1，不符合题目要求，因此我们需要跳过这种情况。
	 */

参考代码：

package 西湖算法题解___中等题;

public class __457环形数组是否存在循环 {
	/*
	题目翻译：
		就是说，有一个数组，可以认为是形成了环的数组
		里面的元素，【正数】代表向前移动多少个，【负数】代表向后退多少个

		问？！
			其中是否存在部分子数组能构成一个循环移动保持不变顺序的数组
	 */
	public boolean circularArrayLoop(int[] nums) {
		/**
		 怎么实现数组循环？     -> 取模移动
		 怎么判断是否能构成循环？   -> 快慢指针


		 -1、我们可以将环形数组理解为图中的 n个点，nums[i] 表示 i号点向 (i+nums[i]) mod n号点连有一条单向边。
		 -2、注意到这张图中的每个点有且仅有一条出边，这样我们从某一个点出发，沿着单向边不断移动，最终必然会进入一个环中。
		 而依据题目要求，我们要检查图中是否存在一个所有单向边方向一致的环。
		 我们可以使用在无向图中找环的一个经典算法：快慢指针。
		 -3、具体地，我们检查每一个节点，令快慢指针从当前点出发，快指针每次移动两步，慢指针每次移动一步，期间每移动一次，
		 我们都需要检查当前单向边的方向是否与初始方向是否一致，如果不一致，我们即可停止遍历，
		 因为当前路径必然不满足条件。为了降低时间复杂度，我们可以标记每一个点是否访问过，过程中如果我们的下一个节点为已经访问过的节点，则可以停止遍历。
		 -4、在实际代码中，我们无需新建一个数组记录每个点的访问情况，而只需要将原数组的对应元素置零即可（题目保证原数组中元素不为零）。
		 遍历过程中，如果快慢指针相遇，或者移动方向改变，那么我们就停止遍历，并将快慢指针经过的点均置零即可。
		 -5、特别地，当 nums[i]为 n 的整倍数时，i的后继节点即为 i 本身，此时循环长度 k=1，不符合题目要求，因此我们需要跳过这种情况。
		 */
		int nLength = nums.length;
		for (int i=0;i<nLength;i++){
			if (nums[i] == 0){
				continue;
			}
			int slowP = i,fastP = cirNext(nums,i);
			//判断非零且方向要求相同
			while (nums[slowP] * nums[fastP] > 0  && nums[slowP] * nums[cirNext(nums,fastP)] > 0){
				if (slowP == fastP){
					if (slowP != cirNext(nums,slowP)){
						return true;
					}else {
						break;
					}
				}
				slowP = cirNext(nums,slowP);
				fastP = cirNext(nums,cirNext(nums,fastP));
			}
			int add = i;
			while (nums[add] * nums[cirNext(nums,add)] > 0){
				int temp = add;
				add = cirNext(nums,add);
				nums[temp] = 0;
			}
		}
		return false;
	}

	/**
	 * 模拟数组循环，即对数值进行取模判断
	 *
	 * @param nums
	 * @param curP
	 * @return
	 */
	private int cirNext(int[] nums, int curP) {
		int nLength = nums.length;
		return ((curP + nums[curP]) % nLength + nLength)%nLength;
	}
}