题目

给你一棵二叉树的根节点，返回该树的 直径 。

二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

两节点之间路径的 长度 由它们之间边数表示。

示例 1：

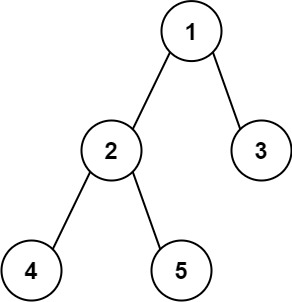
输入：root = [1,2,3,4,5]
输出：3
解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。

示例 2：

输入：root = [1,2]
输出：1

提示：

• 树中节点数目在范围 [1, 10^4] 内
• -100 <= Node.val <= 100

 

解答

源代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int max = 0;

    public int diameterOfBinaryTree(TreeNode root) {
        depth(root);
        return max;
    }

    public int depth(TreeNode node) {
        if (node == null) {
            return 0;
        }

        int left = depth(node.left);
        int right = depth(node.right);
        max = Math.max(max, left + right);

        return Math.max(left, right) + 1;
    }
}

总结

按理还是以每个节点作输入进行递归，但是这道题没办法直接让递归返回的就是我们需要的结果。因为我们想要求的直径肯定包括一个节点（我们设为A）的左右两条边，但是递归再向上返回时，A节点的父节点只需要A的一条边。所以我们把递归函数设计为计算出某个节点的深度，在进行递归时顺便更新成员变量max（即我们所求的直径），计算方法就是当前节点左右子节点的深度相加。