2.1 Lattice Vibration 晶格振动
Born-Oppenheimer Approximation
- Electrons’ movement: Electron theory
- free electron theory
- energy band theory
- Atoms’ movement
- crystal dynamics
- lattice vibration
当研究电子运动时,忽略原子运动;当研究原子运动时,忽略电子运动。
原子运动影响晶体的热、磁、光、超导性质,晶格动力学正是研究原子运动的规律。
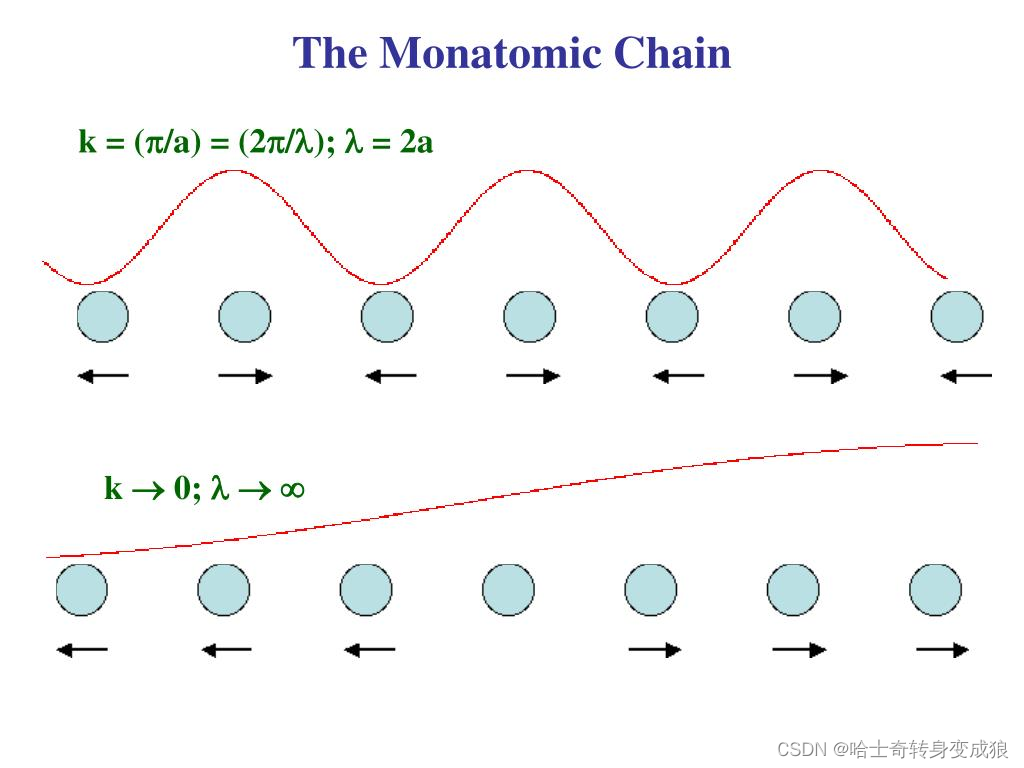
2.1.1 1D Monoatomic Chain 一维单原子链

(1) Equation of motion 运动方程
m u ¨ n = β ( u n + 1 − 2 u n + u n − 1 ) m \ddot u_n = \beta (u_{n+1} - 2u_n + u_{n-1}) mu¨n=β(un+1−2un+un−1)
Two Basic Hypothesises
-
简谐振动假设 Harmonic approximation (Harmonic limit): The restoring force on each atom is approximately proportional to its displacement.
F = − β x F= - \beta x F=−βx -
最近邻假设 Nearest-neighbor limit: To calculate the forces simply, only nearest-neighbor interactions of atoms be considered.
如何计算β: Taylor’s series
Atom potential U( r ):
U ( r ) = U ( a ) + ( r − a ) 2 2 ( d 2 U d r 2 ) r = a + … U(r) = U(a) + \frac{(r-a)^2}{2} \left (\frac{d^2 U}{ d r^2} \right )_{r=a} + \dots U(r)=U(a)+2(r−a)2(dr2d2U)r=a+…
F = − d U ( r ) d r = − [ d 2 U ( r ) d r 2 ] ⋅ ( r − a ) = − β x F = - \frac{d U(r)}{dr} = - \left [ \frac{d^2 U(r)}{dr^2} \right ]\cdot (r-a) = - \beta x F=−drdU(r)=−[dr2d2U(r)]⋅(r−a)=−βx
∴ β = ( d 2 U d r 2 ) r = a \therefore \beta = \left ( \frac{d^2 U}{dr^2} \right) _{r=a} ∴β=(dr2d2U)r=a
β \beta β is the force constant between nearest-neighbor atoms. It will differ for longitudinal and transverse waves in 3D space. (β可以区分横波和纵波)
(2) Born-Karman boundary condition, Periodic boundary condition 周期性边界条件
假设单原子链是无限延伸的,再空间中构成单原子环。这是一种近似,由于原子个数N很大,可以忽略首尾,从而得到周期性边界条件: u N + 1 = u 1 , u N + n = u n u_{N+1} = u_1, \ \ u_{N+n} = u_n uN+1=u1, uN+n=un
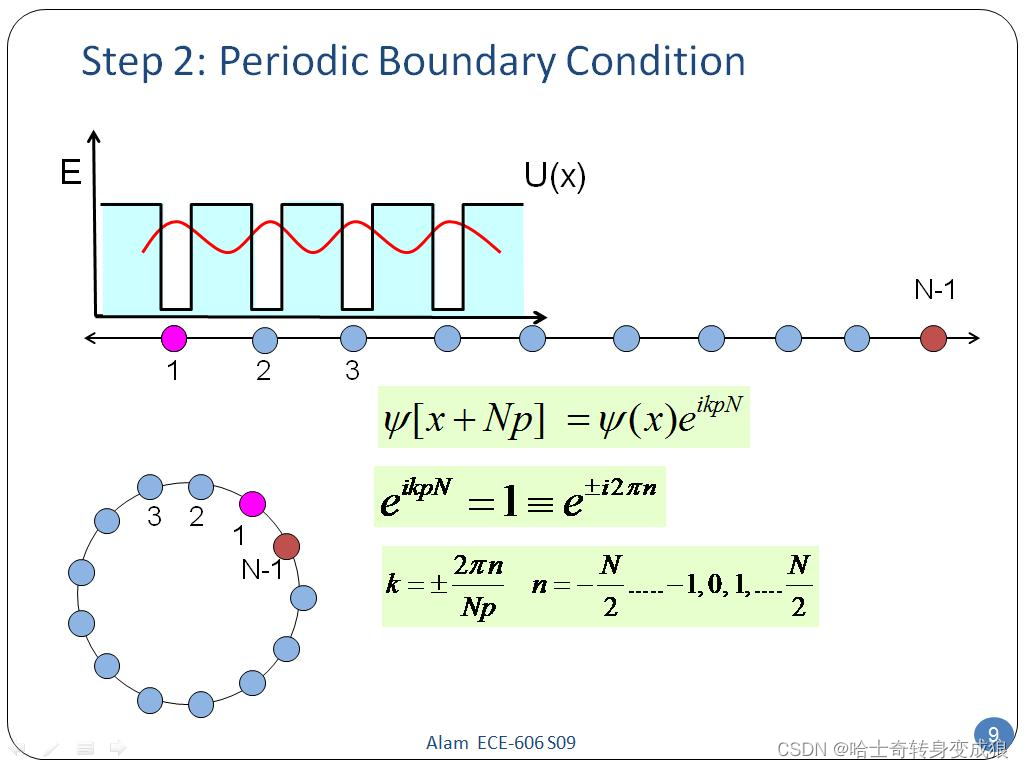
m u ¨ n = β ( u n + 1 − 2 u n + u n − 1 ) m \ddot u_n = \beta (u_{n+1} - 2u_n + u_{n-1}) mu¨n=β(un+1−2un+un−1)
u ¨ n = − ω 2 u n \ddot u_n = - \omega^2 u_n u¨n=−ω2un
u n = A e i ( k x n − ω t ) = A e i ( n a k − ω t ) u_n = A e^{i(kx_n-\omega t)} = Ae^{i(nak-\omega t)} un=Aei(kxn−ωt)=Aei(nak−ωt)
∴ m ω 2 = 2 β ( 1 − cos k a ) \therefore m \omega^2 = 2\beta (1-\cos{ka}) ∴mω2=2β(1−coska)
(3) dispersion relation and lattice wave 色散关系和格波
solve the equation above, then:
ω = 2 β m ∣ sin k a 2 ∣ \omega = 2\sqrt{\frac{\beta}{m}} \left | \sin{\frac{ka}{2}} \right | ω=2mβ sin2ka
k = 2 π N a m , m = 0 , ± 1 , ± 2 , … k=\frac{2\pi}{Na}m, \ \ \ m=0, \pm1, \pm2,\dots k=Na2πm, m=0,±1,±2,…
其中,N:单原子链的原子个数(长度),a:晶格常数
相速度(通常意义上的速度): v ϕ = λ T = ω λ 2 π = ω k = 2 β m ∣ sin k a 2 ∣ k v_{\phi} = \frac{\lambda}{T} = \frac{\omega \lambda}{2 \pi} = \frac{\omega }{k} = 2\sqrt{\frac{\beta}{m}}\frac{\left |\sin \frac{ka}{2} \right |}{k} vϕ=Tλ=2πωλ=kω=2mβk sin2ka
群速度(多列波叠加,波的包络前进的速度): v k = d ω d k = a β m cos k a 2 v_k = \frac{d \omega}{d k} = a \sqrt{\frac{\beta}{m}}\cos \frac{ka}{2} vk=dkdω=amβcos2ka
波速与波长有关的现象叫做色散。
k取值不连续,对应不同的振动模式。
ω 0 = β m , ω M = 2 ω 0 , ω m = 0 \omega_0 = \frac{\beta}{m}, \ \ \ \omega_M = 2\omega_0,\ \ \ \omega_m = 0 ω0=mβ, ωM=2ω0, ωm=0
晶体振动以格波的形式体现,表现为一种集体行为。一组格波代表一组振动模式,即一组 ( k , ω ) (k,\omega) (k,ω)的取值.
independent lattice wave
ω ( k ) = ω ( k + G ) , G = m ⋅ 2 π a i ^ \omega(k) = \omega(k+G), \ \ \ G=m\cdot \frac{2\pi}{a} \hat i ω(k)=ω(k+G), G=m⋅a2πi^
The movement of atoms with k or k+G is the same. So only consider k in 1st BZ.
All independent vibrations are described by k inside BZ.
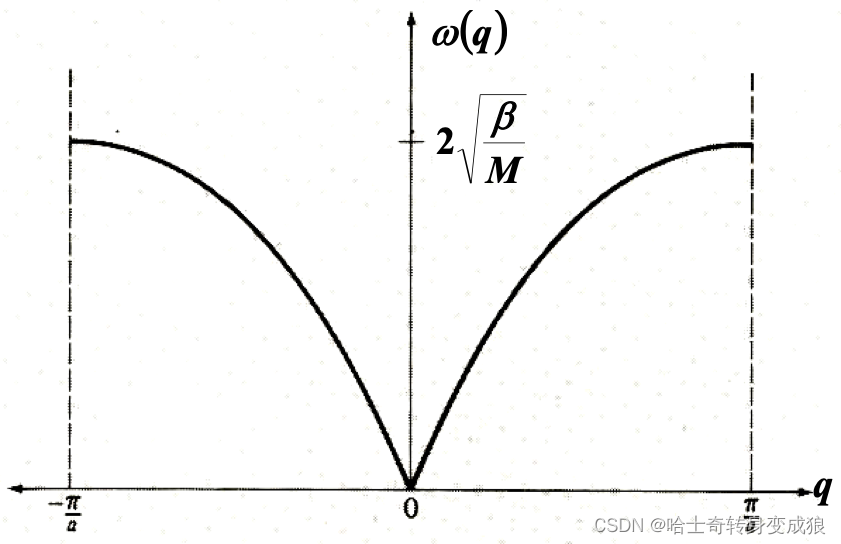
(1)波矢端点落在布里渊区界面上,行波不再传播(驻波),相邻原子的振动方向相反,满足布拉格定律。
k
=
π
a
k=\frac{\pi}{a}
k=aπ
(2)长波极限,相速度=群速度,与波长无关,此时的格波是一种弹性波,晶格可看作连续介质(声波)
λ
≫
a
,
v
ϕ
=
v
k
=
a
β
m
\lambda \gg a, \ \ \ v_{\phi} = v_k = a \sqrt{\frac{\beta}{m}}
λ≫a, vϕ=vk=amβ
2.1.2 1D Diatomic Chain 一维双原子链
(1) equation of motion

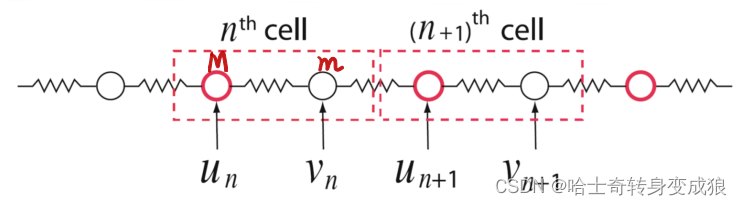
{
M
u
¨
n
=
β
(
ν
n
+
ν
n
−
1
−
2
u
n
)
m
ν
¨
n
=
β
(
u
n
+
u
n
+
1
−
2
ν
n
)
\begin{cases} M \ddot u_n = \beta (\nu_n +\nu_{n-1} - 2u_n) \\ m \ddot \nu _n = \beta (u_n + u_{n+1} - 2\nu_n) \end{cases}
{Mu¨n=β(νn+νn−1−2un)mν¨n=β(un+un+1−2νn)
u N + 1 = u 1 , ν N + n = ν n u_{N+1} = u_1, \ \ \ \nu_{N+n} = \nu_n uN+1=u1, νN+n=νn
u n = A e i ( n a k − ω t ) , ν n = B e i [ n + 1 2 a k − ω t ] u_n = A e^{i(nak - \omega t)}, \ \ \ \nu_n = Be^{i \left [ \frac{n+1}{2} ak - \omega t \right ]} un=Aei(nak−ωt), νn=Bei[2n+1ak−ωt]
代入运动方程可以得到线性齐次代数方程组:
{ ( 2 β − M ω 2 ) A − 2 β cos ( 1 2 a k ) B = 0 − 2 β cos ( 1 2 a k ) A + ( 2 β − m ω 2 ) B = 0 \begin{cases} (2\beta - M \omega^2) A - 2\beta \cos(\frac{1}{2}ak) B = 0 \\ -2\beta \cos(\frac{1}{2}ak) A + (2\beta - m \omega^2) B=0 \end{cases} {(2β−Mω2)A−2βcos(21ak)B=0−2βcos(21ak)A+(2β−mω2)B=0
线性齐次代数方程组有非零解,则系数行列式为0,从而得到:
∣ 2 β − M ω 2 − 2 β cos ( 1 2 a k ) − 2 β cos ( 1 2 a k ) 2 β − m ω 2 ∣ = 0 \begin{vmatrix} 2\beta - M \omega^2 & - 2\beta \cos(\frac{1}{2}ak) \\ -2\beta \cos(\frac{1}{2}ak) & 2\beta - m \omega^2 \end{vmatrix} = 0 2β−Mω2−2βcos(21ak)−2βcos(21ak)2β−mω2 =0
(2) dispersion relation 色散关系
ω ± 2 = β ( M + m ) M m { 1 ± 1 − 4 M m ( M + m ) 2 sin 2 ( 1 2 a k ) } \omega_{\pm}^2 = \frac{\beta (M+m)}{ Mm } \left \{ 1 \pm \sqrt{ 1 - \frac{4Mm}{(M+m)^2} \sin^2{(\frac{1}{2}ak}) } \right \} ω±2=Mmβ(M+m){1±1−(M+m)24Mmsin2(21ak)}
ω
±
2
=
β
M
m
[
(
M
+
m
)
±
M
2
+
m
2
+
2
M
m
cos
(
a
k
)
]
\omega_{\pm} ^2 =\frac{\beta}{Mm}[(M+m) \pm \sqrt{ M^2 + m^2 + 2Mm\cos{(ak)} }]
ω±2=Mmβ[(M+m)±M2+m2+2Mmcos(ak)]
k
=
2
π
N
a
m
,
,
m
=
0
,
±
1
,
±
2
,
…
k=\frac{2\pi}{Na} m,\ \ \ ,m = 0,\pm 1, \pm 2, \dots
k=Na2πm, ,m=0,±1,±2,…
一个k 对应两个ω: ω + , ω − \omega_+,\ \ \omega_- ω+, ω−
一维双原子链有两个格波:光学支(Optical Branch)、声学支(Acoustical Branch)
- 光学支:一个原胞中的两个原子振动方向相反。有明显的光学特征——共振吸收。
- 声学支:一个原胞中的两个原子振动方向相同。弹性波,色散关系简单,原胞可看作一个整体。

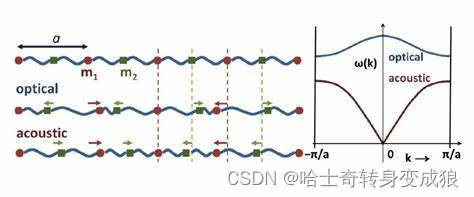
comparation with 1D monoatomic chain and 1D diatomic chain:
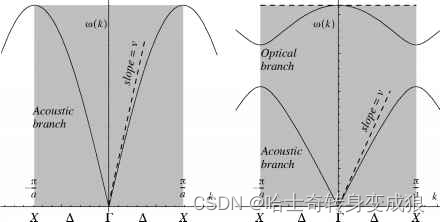

2.1.3 3D Crystal 三维晶体
(1) lattice waves
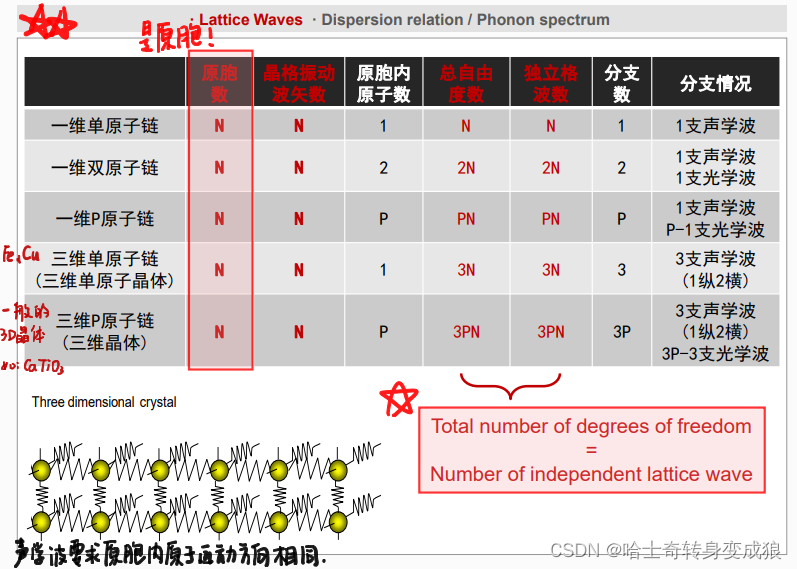
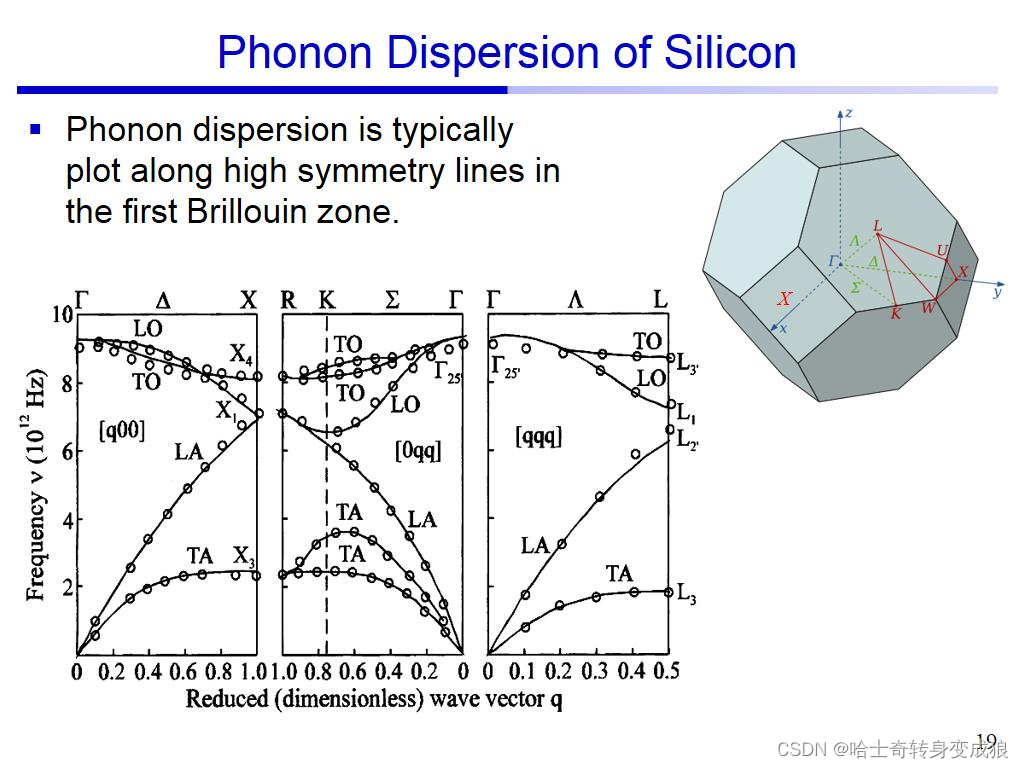
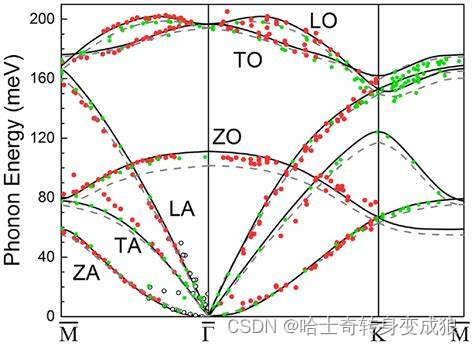
(2) dispersion relation/ Phonon spectrum 一些典型晶体的色散关系/声子能量谱
硅:
石墨:
2.1.4 Quantization of Lattice Waves 格波能量量子化——声子
(1) density of k distribution in k space 波矢k在波矢空间的分布密度
volume of 1st BZ: v b = ( 2 π ) 3 v a v_b = \frac{(2\pi)^3}{v_a} vb=va(2π)3
number of k in 1st BZ:
3D: ρ ( k ) = N ( 2 π ) 3 v a = V ( 2 π ) 3 \rho (k) = \frac{N}{ \frac{(2\pi)^3}{v_a} } = \frac{V}{(2\pi)^3} ρ(k)=va(2π)3N=(2π)3V
V: volume of the primitive unit cell
1D: ρ ( k ) = N a 2 π = L 2 π \rho (k) = \frac{Na}{2\pi} = \frac{L}{2\pi} ρ(k)=2πNa=2πL
2D: ρ ( k ) = S ( 2 π ) 2 \rho(k) = \frac{S}{(2\pi)^2} ρ(k)=(2π)2S
(2) equivalence,将振动模式与谐振子等价
equivalence between a vibration mode and a harmonic oscillator
The energy of crystal corresponding to vibrarion mode k will be
E
k
=
T
k
+
U
k
=
1
2
p
k
2
+
1
2
ω
2
q
k
2
E_k = T_k + U_k = \frac{1}{2}p_k^2+\frac{1}{2}\omega^2 q_k^2
Ek=Tk+Uk=21pk2+21ω2qk2
which is the energy of a harmonic oscillator with displacement
q
k
q_k
qk, momentum
p
k
p_k
pk and vibration frequency
ω
\omega
ω.
This tells us the equivalence between the energy of a vibration mode and the energy of a harmonic oscillator. Crystal lattice vibration energy of a monoatomic chain contain N atoms can be expressed as the summation of the energy of N harmonic oscillators.
A 3D monoatomic crystal: E = T + U = 1 2 ∑ k = 1 3 N ( p k 2 + ω k 2 q k 2 ) E = T+U = \frac{1}{2} \sum_{k=1}^{3N} (p_k^2 + \omega_k^2 q_k^2) E=T+U=21k=1∑3N(pk2+ωk2qk2)
Crystal lattice vibration energy of a 3D monoatomic crystal contain N atoms can be expressed as the summation of the energy of 3N harmonic oscillator, whose frequencies are just the frequencies of the 3N independent vibration modes.
( k , ω ) ⟷ ω ( k ) (k, \omega) \longleftrightarrow \omega (k) (k,ω)⟷ω(k)
独立格波 ⟷ \longleftrightarrow ⟷ 独立的振动模式 ⟷ \longleftrightarrow ⟷ 谐振子
(3) phonon 声子
Energy of a harmonic oscillator with angular frequency ω \omega ω: KaTeX parse error: Undefined control sequence: \E at position 1: \̲E̲= ( n + \frac{1…
Energy of a vibration mode or a lattice wave with angular frequency ω j ( k ) \omega_j (k) ωj(k): E j ( k ) = ( n j ( k ) + 1 2 ) ℏ ω j ( k ) , n j ( k ) = 0 , 1 , 2 , … E_j(\mathbf{k}) = (n_j(\mathbf{k}) + \frac{1}{2}) \hbar \omega_j (\mathbf{k}), \ \ \ n_j(\mathbf{k})= 0, 1, 2,\dots Ej(k)=(nj(k)+21)ℏωj(k), nj(k)=0,1,2,…
Total Energy of lattice vibration of a crystal with N unit cells, each cell having P atoms: E = ∑ j = 1 3 P ∑ k = 1 N E j ( k ) = ∑ j = 1 3 P ∑ k = 1 N ( n j ( k ) + 1 2 ) ℏ ω j ( k ) E = \sum_{j=1}^{3P} \sum_{k=1}^{N} E_j (\mathbf{k}) = \sum_{j=1}^{3P} \sum_{k=1}^{N} (n_j(\mathbf{k}) + \frac{1}{2}) \hbar \omega_j(\mathbf{k}) E=j=1∑3Pk=1∑NEj(k)=j=1∑3Pk=1∑N(nj(k)+21)ℏωj(k)
声子 phonon: ℏ ω j ( k ) \hbar \omega_j (\mathbf{k}) ℏωj(k)
光子 photon: h ν , ℏ ω h\nu, \ \ \hbar \omega hν, ℏω
- ℏ ω j ( k ) \hbar \omega_j (\mathbf{k}) ℏωj(k)是格波能量的激发单元,称为“元激发”;声子是一种准粒子,具有动量 ℏ k ^ \hbar \hat k ℏk^,但并不是光子、电子这样的真实粒子。
- 声子只存在于晶体中,而不能脱离晶体存在。
- 声子动量为准动量,格波的传播并不伴随着质量的定向运动。
- 声子数量可以变化: n j ( k ) n_j(\mathbf{k}) nj(k)。
- 声子是玻色子,遵循Bose-Einstain分布。
(4) lattice vibration energy 晶格振动能
E j ( k ) = ( n j ( k ) + 1 2 ) ℏ ω j ( k ) , n j ( k ) = 0 , 1 , 2 , … E_j(\mathbf{k}) = (n_j(\mathbf{k}) + \frac{1}{2}) \hbar \omega_j (\mathbf{k}), \ \ \ n_j(\mathbf{k})= 0, 1, 2,\dots Ej(k)=(nj(k)+21)ℏωj(k), nj(k)=0,1,2,…
k B k_B kB :Boltzmann constant
Average energy of harmonic oscillators with angular frequency ω j \omega_j ωj at temperature T: E ˉ i = 1 2 ℏ ω i + ℏ ω i 1 e ℏ ω i k B T − 1 = ( 1 2 + 1 e ℏ ω i k B T − 1 ) ℏ ω i \bar E_i = \frac{1}{2} \hbar \omega_i + \hbar \omega_i \frac{1}{e^{\frac{\hbar \omega_i}{k_B T} - 1}} = \left (\frac{1}{2} + \frac{1}{e^{\frac{\hbar \omega_i}{k_B T} - 1}} \right) \hbar \omega_i Eˉi=21ℏωi+ℏωiekBTℏωi−11=(21+ekBTℏωi−11)ℏωi
T=0K: Zero-point energy: 零点能
E
ˉ
i
=
1
2
ℏ
ω
i
\bar E_i = \frac{1}{2}\hbar \omega_i
Eˉi=21ℏωi
T
≫
0
K
T \gg 0K
T≫0K:
ℏ
ω
≪
k
B
T
\hbar \omega \ll k_B T
ℏω≪kBT: 与温度有关的晶格振动能
E
ˉ
i
=
1
2
ℏ
ω
+
k
B
T
≈
k
B
T
\bar E_i = \frac{1}{2} \hbar \omega + k_B T \approx k_B T
Eˉi=21ℏω+kBT≈kBT
Total lattice vibration energy of a crystal: E = ∑ i E ˉ i = ∑ i ( 1 2 + 1 e ℏ ω i k B T − 1 ) = ∑ i 1 2 ℏ ω i + ∑ i ℏ ω i e ℏ ω i k B T − 1 = E 0 + E ( T ) E = \sum_i \bar E_i = \sum_i \left( \frac{1}{2} + \frac{1}{e^{\frac{\hbar \omega_i}{k_B T} - 1}} \right ) = \sum_i \frac{1}{2}\hbar \omega_i + \sum_i \frac{\hbar \omega_i}{e^{\frac{\hbar \omega_i}{k_B T} - 1}} =E_0 +E(T) E=i∑Eˉi=i∑(21+ekBTℏωi−11)=i∑21ℏωi+i∑ekBTℏωi−1ℏωi=E0+E(T)
The problem is that the summation is very difficult to obtain cause the number of independent lattice waves or equivalent harmonic oscillators is very large ( 1 0 23 10^{23} 1023). We need a new concept called “Density of state” to change the summation into integration.
将求和转变为积分
(5) density of states 态密度
The density of states g(ω) is defined as the number of oscillators (or k) per unit
frequency interval.
态密度的定义:单位频率间隔谐振子(振动模式)的数量
g ( ω ) = d n d ω g(\omega) = \frac{dn}{d\omega} g(ω)=dωdn
Total number of oscillators: ∫ 0 ω m g ( ω ) d ω = d N p \int_0^{\omega_m} g(\omega )d\omega = dNp ∫0ωmg(ω)dω=dNp
where d is dimension, N is unit cell number and p is atom number in a cell.
E 0 = ∫ 0 ω m 1 2 ℏ ω g ( ω ) d ω E_0 = \int_0^{\omega_m} \frac{1}{2} \hbar \omega g(\omega )d\omega E0=∫0ωm21ℏωg(ω)dω
E ( T ) = ∫ 0 ω m ℏ ω e ℏ ω k B T − 1 g ( ω ) d ω E(T) = \int_0^{\omega_m} \frac{\hbar \omega}{e^{\frac{\hbar \omega}{k_B T} - 1}} g(\omega )d\omega E(T)=∫0ωmekBTℏω−1ℏωg(ω)dω
∴ E = E 0 + E ( T ) \therefore E = E_0 + E(T) ∴E=E0+E(T)
For one branch of the dispersion relation:
d
n
=
g
j
(
ω
)
d
ω
=
ρ
j
(
k
)
d
k
dn=g_j(\omega) d\omega =\rho_j(k)dk
dn=gj(ω)dω=ρj(k)dk
ρ
j
(
k
)
=
{
L
2
π
,
1D
S
4
π
2
,
2D
V
8
π
3
,
3D
\rho_j(k) = \begin{cases} \frac{L}{2\pi}, & \text{1D} \\ \frac{S}{4\pi^2}, & \text{2D} \\ \frac{V}{8\pi^3}, & \text{3D} \end{cases}
ρj(k)=⎩
⎨
⎧2πL,4π2S,8π3V,1D2D3D
g j ( ω ) = ρ j ( k ) d k d ω j g_j(\omega) = \rho_j(k) \frac{dk}{d\omega_j} gj(ω)=ρj(k)dωjdk
g ( ω ) = ∑ j = 1 d p g j ( ω ) g(\omega) = \sum_{j=1}^{dp} g_j(\omega) g(ω)=j=1∑dpgj(ω)
lattice vibration ~ harmonic oscillator ~ phonon