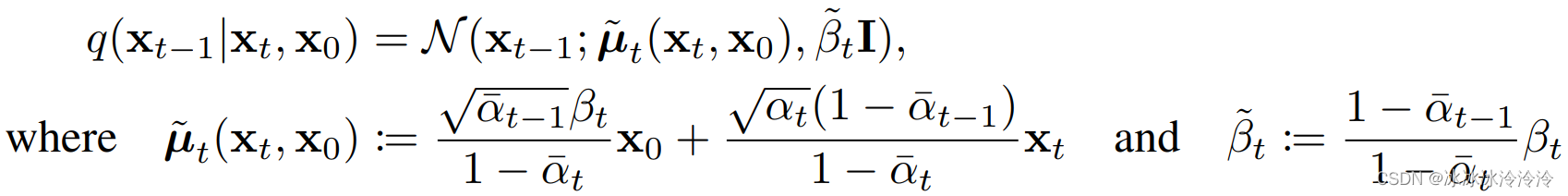小结：本文主要讲述vtk中vtkCleanPolyData过滤器的作用和实现原理，希望对各位小伙伴能有所帮助！

 

示例：

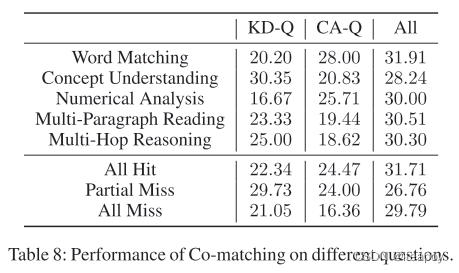
将下图进行Clean，设置Tolerance为0.01（相对误差）。

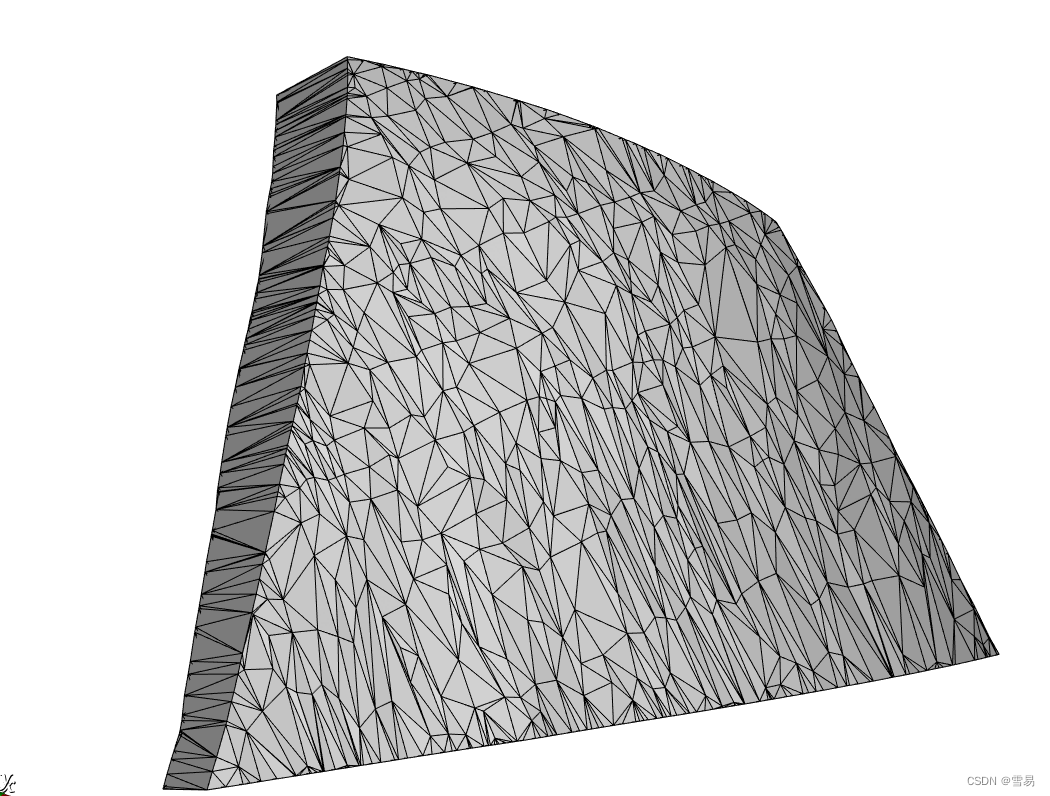
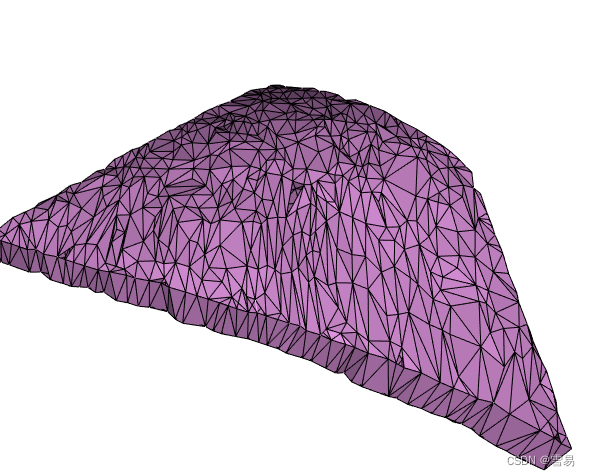
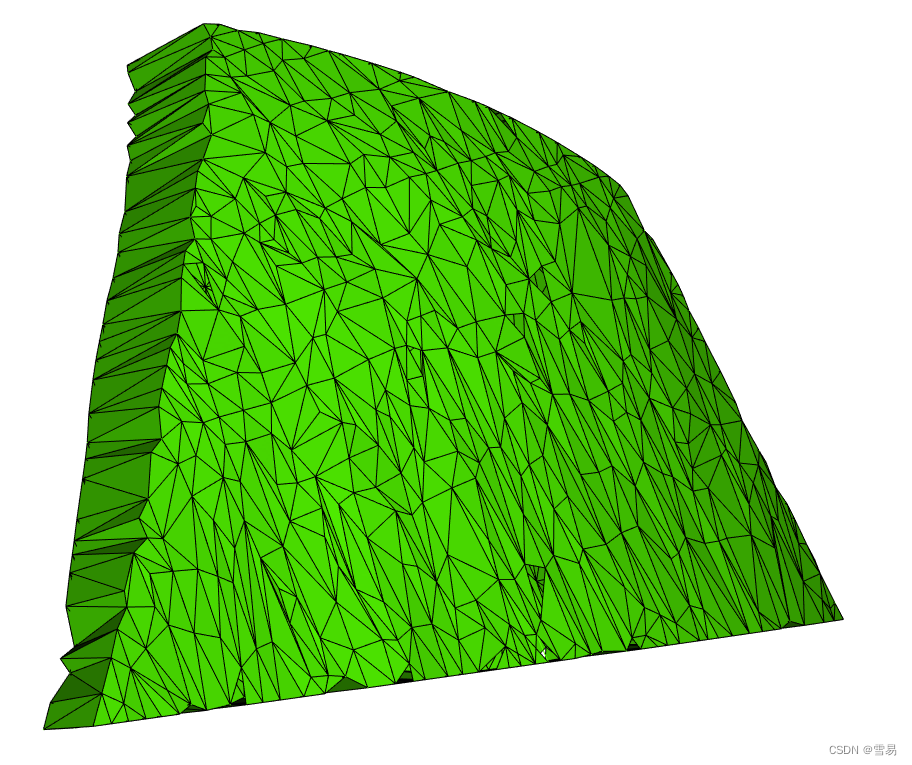
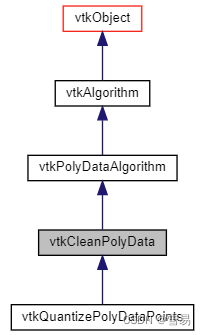
                    vtkCleanPolyData                                 vtkQuantizePolyDataPoints

 

 结论：会删除掉一些特征点，会出现空洞。

vtkCleanPolyData

描述：合并重复点，删除未使用的点，删除退化单元格

vtkCleanPolyData是一个过滤器，它将多边形数据作为输入输出。vtkCleanPolyData将合并重复点(启用并在指定的容差范围内)，消除任何单元格中没有使用的点（启用），将退化单元格转换为适当的形式(例如，如果合并三角形的两个点，则将三角形转换为直线)。

Line with 1 points -> Vert (if ConvertLinesToPoints)
Poly with 2 points -> Line (if ConvertPolysToLines)
Poly with 1 points -> Vert (if ConvertPolysToLines && ConvertLinesToPoints)
Strp with 3 points -> Poly (if ConvertStripsToPolys)
Strp with 2 points -> Line (if ConvertStripsToPolys && ConvertPolysToLines)
Strp with 1 points -> Vert (if ConvertStripsToPolys && ConvertPolysToLines  && ConvertLinesToPoints)
 

只有当ConvertLinesToPoints开启且所有点合并为一个时，类型为VTK_POLY_LINE的单元格才会被转换为顶点。退化线段(有两个相同的端点)将被删除。

注意事项

1. 点的合并可以被禁用。在这种情况下，将不使用点定位器，并且将消除没有被任何单元格使用的点，但永远不会合并。

2. 合并点可以改变拓扑结构，包括引入non-manifold形式。为了避免这些问题，应仔细选择公差。子类应该处理OperateOnBounds和OperateOnPoint，以确保定位器被正确初始化(即所有修改的点必须位于修改的边界内)。

3. 当对一组没有单元格的坐标进行操作，则必须在使用vtkCleanPolyData过滤器之前，将包含所有点的vtkPolyVertex单元格添加到PolyData(或使用vtkVertexGlyphFilter)。

4. 如果精确地指定公差=0.0，则vtkCleanPolyData将使用vtkMergePoints对象来合并点(这更快)。否则使用较慢的vtkIncrementalPointLocator。

5. 合并重复点的公差可以通过绝对值和可以通过相对值（即包围盒对角线的比例，默认）来进行设定。绝对值通过SetToleranceIsAbsolute和SetAbsoluteTolerance设置。相对值通过SetTolerance设置。

参数

1. ConvertLinesToPoints（默认为True）

2. ConvertPolysToLines（默认为True）

3. ConvertStripsToPolys（默认为True）

4. PointMerging（默认为True）

vtkQuantizesPolyDataPoints

描述：量化点的x,y,z坐标

vtkQuantizePolyDataPoints是vtkCleanPolyData的子类，继承了vtkCleanPolyData的功能，它在插入到点列表之前量化点坐标。用户应该将QFactor设置为正值(默认为0.25)，所有{x,y,z}坐标将被量化为该粒度大小。