文章目录
- 一、随机试验与随机事件
- 1.1 随机试验
- 1.2 样本空间
- 1.3 随机事件
- 二、事件的运算与关系
- 2.1 事件的运算
- 2.2 事件的关系
- 2.3 事件运算的性质
- 三、概率的公理化定义与概率的基本性质
- 3.1 概率的公理化定义
- 3.2 概率的基本性质
- 写在最后
一、随机试验与随机事件
1.1 随机试验
若一个试验满足如下条件:
- 在相同的条件下该试验可重复进行;
- 试验的结果是多样的且所有可能的结果在试验前都是确定的;
- 某次试验之前不确定具体发生的结果,
这样的试验称为随机试验,简称试验,一般用字母 E E E 表示。
1.2 样本空间
设 E E E 为随机试验,随机试验 E E E 的所有可能的基本结果所组成的集合,称为随机试验 E E E 的样本空间,记为 Ω \Omega Ω , Ω \Omega Ω 中的任意一个元素称为样本点。
1,样本空间里面所有的元素必须是最基本的,即不可再分。
2,样本空间必须是所有可能的基本结果,即具有完备性,且同一个基本结果在样本空间中只出现一次。
1.3 随机事件
设 E E E 为随机试验, Ω \Omega Ω 为其样本空间,则 Ω \Omega Ω 的子集称为随机事件,其中 ∅ \emptyset ∅ 称为不可能事件, Ω \Omega Ω 称为必然事件。
二、事件的运算与关系
2.1 事件的运算
设
A
,
B
A,B
A,B 为两个随机事件,则事件
A
A
A 与事件
B
B
B 同时发生的事件,称为事件
A
,
B
A,B
A,B 的积事件,记为
A
B
AB
AB 或
A
⋂
B
A\bigcap B
A⋂B ,如下图所示。

事件
A
A
A 或事件
B
B
B 发生的事件(即事件
A
A
A 与事件
B
B
B 至少有一个事件发生的事件),称为事件
A
,
B
A,B
A,B 的和事件,记为
A
+
B
A+B
A+B 或
A
⋃
B
A\bigcup B
A⋃B ,如下图所示。

事件
A
A
A 发生而事件
B
B
B 不发生的事件,称为事件
A
,
B
A,B
A,B 的差事件,记为
A
−
B
A-B
A−B 。事件
A
A
A 不发生的事件,称为事件
A
A
A 的补事件,记为
A
‾
\overline{A}
A 。
2.2 事件的关系
设 A , B A,B A,B 为两个随机事件,若事件 A A A 发生时,事件 B B B 一定发生,则称 A A A 包含于 B B B ,记为 A ⊂ B A\subset B A⊂B 。若有 A ⊂ B , B ⊂ A A\subset B,B\subset A A⊂B,B⊂A ,称两事件相等,记为 A = B A=B A=B 。
若事件
A
A
A 与
B
B
B 不能同时发生,称事件
A
,
B
A,B
A,B 不相容或互斥,如下图所示。

若事件
A
A
A 与
B
B
B 不能同时发生,但至少会有一个发生,称事件
A
,
B
A,B
A,B 为对立事件,如下图所示。
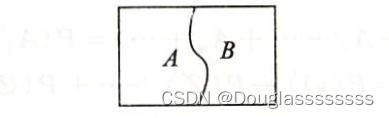
(1) A = ( A − B ) + A B A=(A-B)+AB A=(A−B)+AB ,且 A − B A-B A−B 与 A B AB AB 互斥。
(2) A + B = ( A − B ) + ( B − A ) + A B A+B=(A-B)+(B-A)+AB A+B=(A−B)+(B−A)+AB ,且 A − B , B − A , A B A-B,B-A,AB A−B,B−A,AB 两两互斥。
(3) A B ⊂ A ⊂ A + B , A B ⊂ B ⊂ A + B AB\subset A\subset A+B,AB\subset B\subset A+B AB⊂A⊂A+B,AB⊂B⊂A+B 。
(4)事件 A , B A,B A,B 互斥的充要条件是 A B = ∅ AB=\empty AB=∅ 。
(5)事件 A , B A,B A,B 对立的充要条件是 A B = ∅ AB=\empty AB=∅ ,且 A + B = Ω A+B=\Omega A+B=Ω 。
2.3 事件运算的性质
好多啊,如果要记住的话可费劲了,还容易错,最好还是结合图示来记忆和推吧。
1. A B = B A , A + B = B + A ; AB=BA,A+B=B+A; AB=BA,A+B=B+A;
2.
(
1
)
A
⋃
A
=
A
,
A
⋂
A
=
A
;
(1)A\bigcup A=A,A\bigcap A=A;
(1)A⋃A=A,A⋂A=A;
(
2
)
A
⋂
(
B
⋃
C
)
=
(
A
⋂
B
)
⋃
(
A
⋂
C
)
,
A
⋃
(
B
⋂
C
)
=
(
A
⋃
B
)
⋂
(
A
⋃
C
)
;
(2)A\bigcap(B\bigcup C)=(A\bigcap B)\bigcup (A\bigcap C),A \bigcup (B \bigcap C)=(A\bigcup B) \bigcap (A \bigcup C);
(2)A⋂(B⋃C)=(A⋂B)⋃(A⋂C),A⋃(B⋂C)=(A⋃B)⋂(A⋃C);
3.(1)
A
=
(
A
−
B
)
⋃
A
;
A=(A-B) \bigcup A;
A=(A−B)⋃A;
(
2
)
(
A
−
B
)
⋂
A
=
A
−
B
;
(2)(A-B)\bigcap A=A-B;
(2)(A−B)⋂A=A−B;
(
3
)
A
+
B
=
(
A
−
B
)
⋃
A
B
⋃
(
B
−
A
)
;
(3)A+B=(A-B)\bigcup AB \bigcup (B-A);
(3)A+B=(A−B)⋃AB⋃(B−A);
4.(1)
A
+
A
‾
=
Ω
;
A+\overline{A}=\Omega;
A+A=Ω;
(
2
)
A
⋂
A
‾
=
∅
;
(2)A \bigcap \overline{A} =\empty;
(2)A⋂A=∅;
5.(1)
A
∩
B
‾
=
A
‾
∪
B
‾
;
\overline{A\cap B}=\overline{A}\cup \overline{B};
A∩B=A∪B;
(
2
)
A
‾
∩
B
‾
=
A
∪
B
‾
(2)\overline{A}\cap\overline{B}=\overline{A\cup B}
(2)A∩B=A∪B
第 5 条的结论比较有规律,很像戴帽子和脱帽子,都要变运算。同样有如下运算性质: A ∪ B ‾ = A ‾ ∩ B ‾ , A ‾ ∪ B ‾ = A ∩ B ‾ \overline{A\cup B}=\overline{A}\cap \overline{B},\overline{A}\cup\overline{B}=\overline{A\cap B} A∪B=A∩B,A∪B=A∩B
三、概率的公理化定义与概率的基本性质
3.1 概率的公理化定义
设随机试验 E E E 的样本空间为 Ω \Omega Ω ,在 Ω \Omega Ω 上定义满足如下条件的随机事件的函数 P ( A ) ( A ⊂ Ω ) P(A)(A \subset \Omega) P(A)(A⊂Ω) ,称为事件 A A A 的概率:
(1)(非负性) 对任意的事件 A A A ,有 P ( A ) ≥ 0 ; P(A) \geq 0; P(A)≥0;
(2)(归一性) P ( Ω ) = 1 ; P(\Omega)=1; P(Ω)=1;
(3)(可列可加性) 设 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,则有 P ( ⋃ n = 1 ∞ A n ) = ∑ n = 1 ∞ P ( A n ) , P(\bigcup_{n=1}^{\infty}A_n)=\sum_{n=1}^{\infty}P(A_n), P(n=1⋃∞An)=n=1∑∞P(An), 则对任意的 A ⊂ Ω A\subset \Omega A⊂Ω ,称 P ( A ) P(A) P(A) 为事件 A A A 的概率。
3.2 概率的基本性质
(一)
P
(
∅
)
=
0.
P(\empty)=0.
P(∅)=0.
证明:令
A
1
=
A
2
=
⋯
=
A
n
=
⋯
=
∅
A_1=A_2= \dots=A_n=\dots=\empty
A1=A2=⋯=An=⋯=∅ ,有
A
1
=
A
2
=
⋯
=
A
n
=
…
A_1=A_2= \dots=A_n=\dots
A1=A2=⋯=An=… 互不相容,由可列可加性,有
P
(
A
1
+
A
2
+
⋯
+
A
n
+
…
)
=
P
(
A
1
)
+
P
(
A
2
)
+
…
P
(
A
n
)
+
…
,
P(A_1+A_2+ \dots+A_n+\dots)=P(A_1)+P(A_2)+\dots P(A_n)+\dots,
P(A1+A2+⋯+An+…)=P(A1)+P(A2)+…P(An)+…, 由
A
1
+
A
2
+
⋯
+
A
n
+
⋯
=
∅
A_1+A_2+ \dots+A_n+\dots =\empty
A1+A2+⋯+An+⋯=∅ ,可得
P
(
∅
)
=
P
(
∅
)
+
P
(
∅
)
+
⋯
+
P
(
∅
)
+
…
,
P(\empty)=P(\empty)+P(\empty)+\dots+P(\empty)+\dots ,
P(∅)=P(∅)+P(∅)+⋯+P(∅)+…, 故
P
(
∅
)
=
0
P(\empty)=0
P(∅)=0 。
(二)(有限可加性) 设 A 1 , A 2 , … , A n A_1,A_2,\dots,A_n A1,A2,…,An 为互斥的有限个随机事件列,则 P ( ⋃ k = 1 n A k ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{k=1}^{n}A_k)=\sum_{k=1}^{n}P(A_k). P(k=1⋃nAk)=k=1∑nP(Ak). 证明:取 A n + 1 = A n + 2 = ⋯ = ∅ A_{n+1}=A_{n+2}=\dots=\empty An+1=An+2=⋯=∅ ,则 A 1 , A 2 , … , A n , … A_1,A_2,\dots,A_n,\dots A1,A2,…,An,… 为不相容的随机事件,由 P ( A n + 1 ) = P ( A n + 2 ) = ⋯ = 0 P(A_{n+1})=P(A_{n+2})=\dots=0 P(An+1)=P(An+2)=⋯=0 及可列可加性,可得 P ( ⋃ n = 1 ∞ A n ) = P ( ⋃ k = 1 n A k ) = P ( A 1 ) + P ( A 2 ) + … P ( A n ) = ∑ k = 1 n P ( A k ) . P(\bigcup_{n=1}^{\infty}A_n)=P(\bigcup_{k=1}^{n}A_k)=P(A_1)+P(A_2)+\dots P(A_n)=\sum_{k=1}^{n}P(A_k). P(n=1⋃∞An)=P(k=1⋃nAk)=P(A1)+P(A2)+…P(An)=k=1∑nP(Ak). (三)(补概率的公式) : P ( A ‾ ) = 1 − P ( A ) . P(\overline{A})=1-P(A). P(A)=1−P(A).
写在最后
剩下关于概率的基本公式、独立事件以及贝叶斯和概型,放到下一篇文章吧。