1、目的
项目具体不便透露,主要记录方法的理解与使用。
数据分析工具见上一篇博客
https://blog.csdn.net/qq_36212935/article/details/130849333
2、背景
数据分析,FSC、SSC、SFL数据直方图如下:
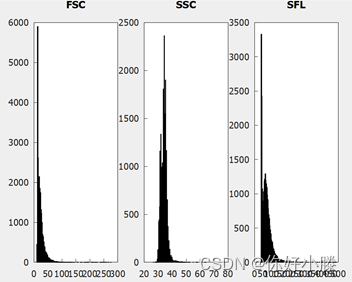
发现SFL数据呈一定“高斯”分布图像,具体数据直方图如下:
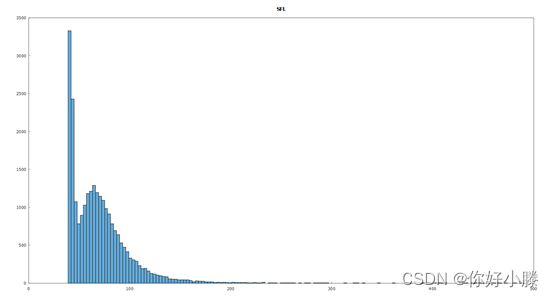
简要理解为:
a>左边“频数”高的,数值低的为杂点,即噪声数据,影响项目最终结果;
b>右边是想得到的数据,但杂点处也包含了得到的数据,如何有效的分离杂点和有效数据是本文需研究的内容,即有效数据的大小应该是多少。
3、方法
(1)GMM方法
python调用相关库实现GaussianMixture算法(简称GMM算法),实现GMM算法聚团分类图像如下:
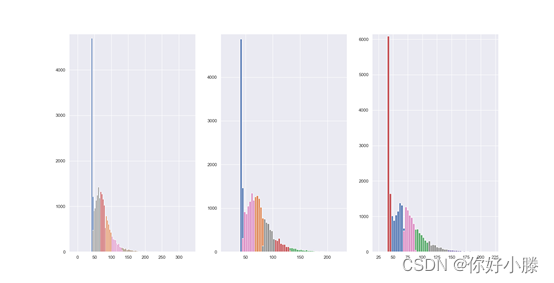
这里选用8个高斯混合而成,杂点处被分类为同一标签,根据给定数据的每个组件的后验概率求得除杂点外的总后验概率之和,图形如下:
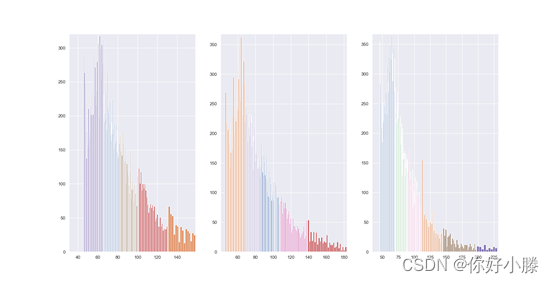
数据结果如下:(左为原始数据重复性,右为GMM算法过滤后的数据重复性)
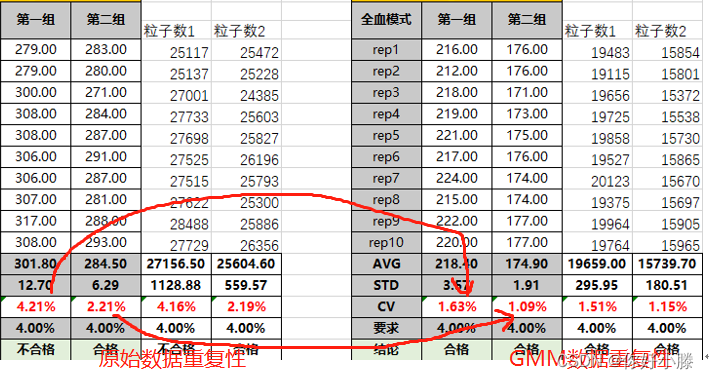
可以看到有效数据(粒子数)变得更小且更稳定,即CV值更低。
(2)非线性拟合方法
非线性拟合方法主要涉及到有效数据混合高斯分布的拟合,其拟合需要的参数值(即a峰值、b横坐标、c标准差)用LM算法求最小值得到。LM算法涉及到雅克比矩阵,黑塞矩阵等概念的应用,代价函数的选取等。最终希望得到一个“较好”的高斯分布函数。如下是2个高斯的部分代码,调用eigen库函数实现:
int ngauss = 2;
Eigen::VectorXd x_init(ngauss * 3);
x_init.setOnes();
x_init *= 50;
x_init(0) = 151;
x_init(1) = 52;
x_init(2) = 32;
x_init(3) = 149;
x_init(4) = 56;
x_init(5) = 31;
DiGaussFunctor functor(ngauss, &input);
Eigen::LevenbergMarquardt<DiGaussFunctor> lmSolver(functor);
Eigen::LevenbergMarquardtSpace::Status status = lmSolver.minimize(x_init);
eigen库用法见:
https://zhuanlan.zhihu.com/p/414383770
最终拟合后的图形如下:
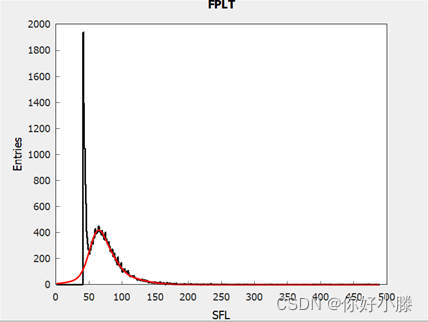
最后,根据此有效数据的高斯分布规律来选取有效数据粒子数。
a>第一种想法是,直方图波谷位置右侧数据直接保留,左侧数据根据高斯分布与原杂点数据差的比值,按0-1的随机数的概率,来选取杂点处的数据作为有效数据,概率小于比值即是有效数据,否则不是。
b、第二种想法是,右侧不变,左侧的粒子数选取根据面积来判断。根据梯形法则求高斯分布的面积,左侧面积比上右侧面积乘以右侧有效粒子数即为左侧该选取的杂点粒子数。
梯形法则见:
https://zhuanlan.zhihu.com/p/629972534#:~:text=%E6%A2%AF%E5%BD%A2%E6%B3%95%E5%88%99%E6%98%AF%E4%B8%80%E7%A7%8D%E6%95%B0%E5%80%BC%E7%A7%AF%E5%88%86%E6%96%B9%E6%B3%95%EF%BC%8C%E7%94%A8%E4%BA%8E%E4%BC%B0%E8%AE%A1%E5%AE%9A%E7%A7%AF%E5%88%86%E7%9A%84%E5%80%BC%E3%80%82%20%E5%AE%83%E5%9F%BA%E4%BA%8E%E5%B0%86%E5%AE%9A%E7%A7%AF%E5%88%86%E7%9A%84%E5%8C%BA%E9%97%B4%20%E5%88%86%E5%89%B2%E6%88%90%E8%8B%A5%E5%B9%B2%E4%B8%AA%E5%B0%8F%E6%A2%AF%E5%BD%A2%20%EF%BC%8C%E4%BB%A5%E9%80%BC%E8%BF%91%E6%9B%B2%E7%BA%BF%E4%B8%8B%E9%9D%A2%E7%A7%AF%EF%BC%8C%E4%BB%8E%E8%80%8C%E5%BE%97%E5%88%B0%E5%AE%9A%E7%A7%AF%E5%88%86%E7%9A%84%E8%BF%91%E4%BC%BC%E5%80%BC%E3%80%82,%E5%85%B7%E4%BD%93%E5%9C%B0%EF%BC%8C%E6%88%91%E4%BB%AC%E5%B0%86%E7%A7%AF%E5%88%86%E5%8C%BA%E9%97%B4%20%5Ba%2C%20b%5D%E7%AD%89%E5%88%86%E6%88%90n%E7%AD%89%E4%BB%BD%EF%BC%8C%E6%AF%8F%E4%B8%80%E4%BB%BD%E9%95%BF%E5%BA%A6%E4%B8%BAh%3D%20%28b-a%29%2Fn%E3%80%82
(3)降维方法+非线性方法
由于非线性拟合使用的数据是单一SFL数据,而最终结果是要使用FSC、SFL上的数据,考虑一种降维方法,保留FSC和SFL上的数据信息,即主成分分析方法PCA,其实现原理见:
https://zhuanlan.zhihu.com/p/37777074
实现步骤为:
1、去中心化;
2、计算协方差矩阵;
3、特征值分解方法求协方差矩阵的特征值与特征向量;
即:
Eigen::EigenSolver<Eigen::Matrix2d> es(sigma);
Eigen::Matrix2d D = es.pseudoEigenvalueMatrix(); //特征值
Eigen::Matrix2d V = es.pseudoEigenvectors();//特征向量
4、特征值从大到小排序,选择其中最大的k个;
5、将数据转换到k个特征向量构建的新空间中。
其相关值为:
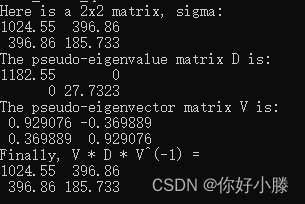
后续还是使用第二种的非线性拟合方法,此时需要注意,降维数据的改变需修改拟合的高斯个数,初始值等,以达到最优的高斯分布。
其结果图如下:
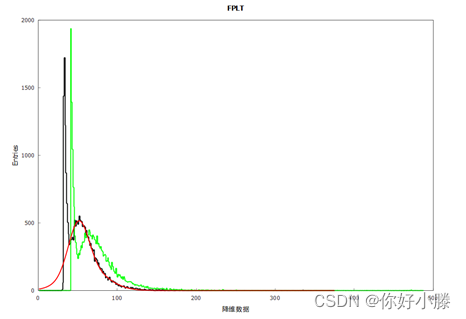
黑色线表示降维数据、绿色线表示SFL单一数据,红色线表示拟合降维数据的高斯分布。降维数据相比SFL数据整体减小,直方图左移。由于降维数据包含更多信息,PLT粒子数更符合“高斯”分布规律,所以使用2个高斯就非常好的拟合出右侧PLT粒子的分布规律。降维数据和拟合高斯分布如下所示:
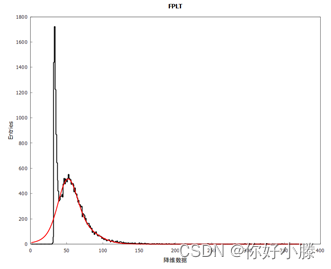
二者对比结果如下:
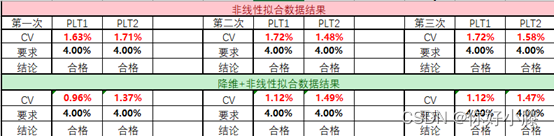
4、总结
三种方法的预研,得到最终数据的对比结果,如下表所示:
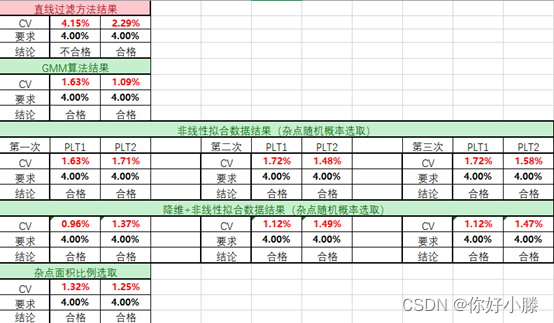
老方法直线过滤不适用,结果最好的是降维方法加上非线性拟合方法的数据结果,杂点选取方法采用面积比例的方法,数据稳定。