题目大意

$1\le n,l_i,r_i\le 5\ast 10^5$

题解

这题 $l/r$ 的数据在 $5\times 10^5$ ，想到差分。
特殊的是它有两条线段，对于同一个点 ，一对线段的贡献可能为 $0/1/2$ 。
相交的线段单点贡献为 $2$ ，不相交的单点贡献为 $1$ 。
我们需要维护 $0/1/2$ 的个数，对所有的点统计答案即可。
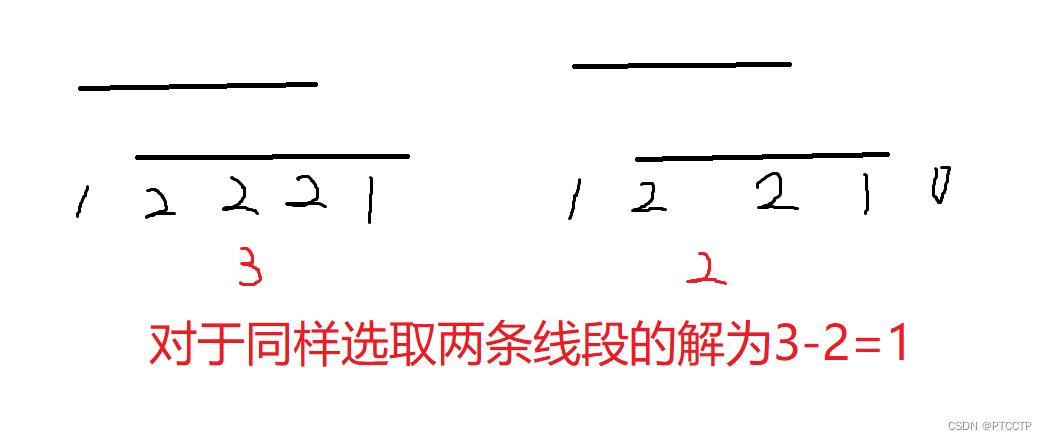
考虑答案中有大量重复，对于一段选择方案相同的线段，应该只选一次，
提供一种新思路：
将每一条线段长度减一，即删去了该线段的一个单点贡献。
再将总答案减去计算后的结果即可，即统计右端点。

参考代码

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=1e9+7;
const int N=5e5+5;
vector<pair<int,int> > f[N],g[N];
int n;
int pow2[N];
ll ans=0;
int main()
{
	pow2[0]=1;
	for(int i=1;i<N;i++)
		pow2[i]=(pow2[i-1]*2)%mod;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		int l1,r1,l2,r2;
		scanf("%d%d%d%d",&l1,&r1,&l2,&r2);
		f[l1].push_back({1,0});
		f[l2].push_back({1,0});
		f[r1+1].push_back({-1,0});
		f[r2+1].push_back({-1,0});
		int l=max(l1,l2),r=min(r1,r2);
		if(l<=r)                   //处理相交的线段
        {
            f[l].push_back({0,1});
		    f[r+1].push_back({0,-1});
        }
		r1--;                      //去除右端点
		r2--;
		g[l1].push_back({1,0});             //差分
		g[l2].push_back({1,0});
		g[r1+1].push_back({-1,0});
		g[r2+1].push_back({-1,0});
        l=max(l1,l2),r=min(r1,r2);
		if(l<=r)               
        {
            g[l].push_back({0,1});
		    g[r+1].push_back({0,-1});
        }
 	}
	int a=0,b=0;
	for(int i=1;i<N;i++)
	{
        for(int j=0;j<f[i].size();j++)
        {
            a+=f[i][j].first;
		    b+=f[i][j].second;
        }
		if(a-b==n)                      //有n条不是一对的线段重合
			ans=(ans+pow2[b])%mod;
	}
	a=0,b=0;
//    cout<<ans<<endl;
	for(int i=1;i<N;i++)
	{
        for(int j=0;j<g[i].size();j++)
        {
            a+=g[i][j].first;
		    b+=g[i][j].second;
        }
		if(a-b==n)
			ans=((ans-pow2[b]+mod)%mod+mod)%mod;
	}
	printf("%lld\n",ans);
}