【一】常见的使用树的场景

以树状结构表示和存储数据是软件开发中的常见问题：
（1）XML / Markup语法解析器（例如Apache Xerces和Xalan XSLt）使用树
（2）PDF使用以下树结构：根节点->目录节点->页面节点->子页面节点。通常，PDF文件在内存中表示为平衡树
（3）多种科学和游戏应用程序使用决策树，概率树，行为树；Flare可视化库（http://flare.prefuse.org/）充分利用了生成树，经纪人在决定是否投标合同时也使用树

树是表示层次结构的方法之一，因此可用于许多问题域：
（1）计算机科学中的二叉树
（2）生物学中的系统树
（3）商业中的庞氏骗局
（4）项目管理中的任务分解树
（5）树用于建模多级关系，例如“上级-下级”，“祖先-后代”，“整个-部分”，“一般-特定”

【二】方式一：邻接表

（1）方法介绍

图论中的邻接表是一种通过存储每个顶点的邻居列表（即相邻顶点）来表示图的方法。对于树，可以仅存储父节点，然后每个列表都包含一个值，该值可以与顶点一起存储在数据库中。这是最流行的表示形式之一，也是最直观的表示形式：表仅具有对自身的引用（图2）。然后，根节点NULL的父节点包含一个空值（）。

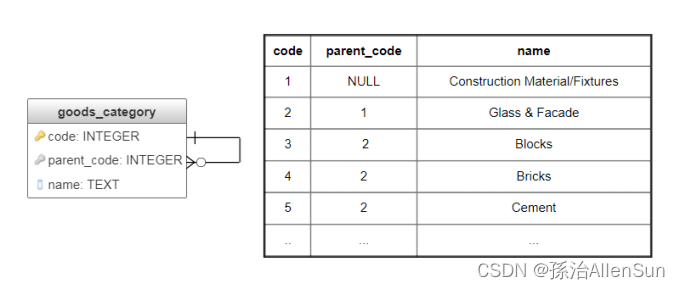
此方法的主要数据选择操作要求DBMS支持递归查询。PostgreSQL支持这种类型的查询，但是对于不支持DBMS的用户，可能需要通过使用临时表和存储过程来执行选择。以下是一些查询示例。

（1）获取给定节点的子树

WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
	SELECT code, name, parent_code, 1 FROM goods_category WHERE code=1 /* id of the given node */
	UNION ALL 
	SELECT c.code, c.name, c.parent_code, level+1
	FROM goods_category c, sub_category sc
	WHERE c.parent_code = sc.code  
)
SELECT code, name, parent_code, level FROM sub_category;

（2）从根到给定节点的路径

WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
	SELECT code, name, parent_code, 1 FROM goods_category WHERE code=5 /* id of the given node */
	UNION ALL 
	SELECT c.code, c.name, c.parent_code, level+1
	FROM goods_category c, sub_category sc
	WHERE c.code = sc.parent_code  
)
SELECT code, name, parent_code, (SELECT max(level) FROM sub_category) - level AS distance FROM sub_category;

（3）检查Cement节点（代码= 5）是否为Construction Material / Fixtures（代码= 1）的后代

WITH RECURSIVE sub_category(code, name, parent_code, level) AS (
	SELECT code, name, parent_code, 1 FROM goods_category WHERE code=5 /* id of the checked node */
	UNION ALL 
	SELECT c.code, c.name, c.parent_code, level+1
	FROM goods_category c, sub_category sc
	WHERE c.code = sc.parent_code  
) 
SELECT CASE WHEN exists(SELECT 1 FROM sub_category WHERE code=2 /* code of the subtree root */)
	THEN 'true' 
	ELSE 'false' 
	END

（2）优点

（1）数据的直观表示（元组(code, parent_code)直接对应于树的边缘）；
（2）没有数据冗余，也不需要非参照完整性约束（除非您需要DBMS级约束来防止循环）；
（3）树木可以有任意深度；
（4）快速，简单的插入，移动和删除操作，因为它们不会影响任何其他节点。

（3）缺点

该方法需要递归以便选择节点的后代或祖先，定义节点的深度，并找出后代的数量。如果DBMS不支持特定功能，则无法有效地实现这些操作。对于无法进行递归或不可行的情况，可以通过使用一个递归来实现此方法的某些优点。

（4）实现案例：生成菜单树结构

数据库的存储方式

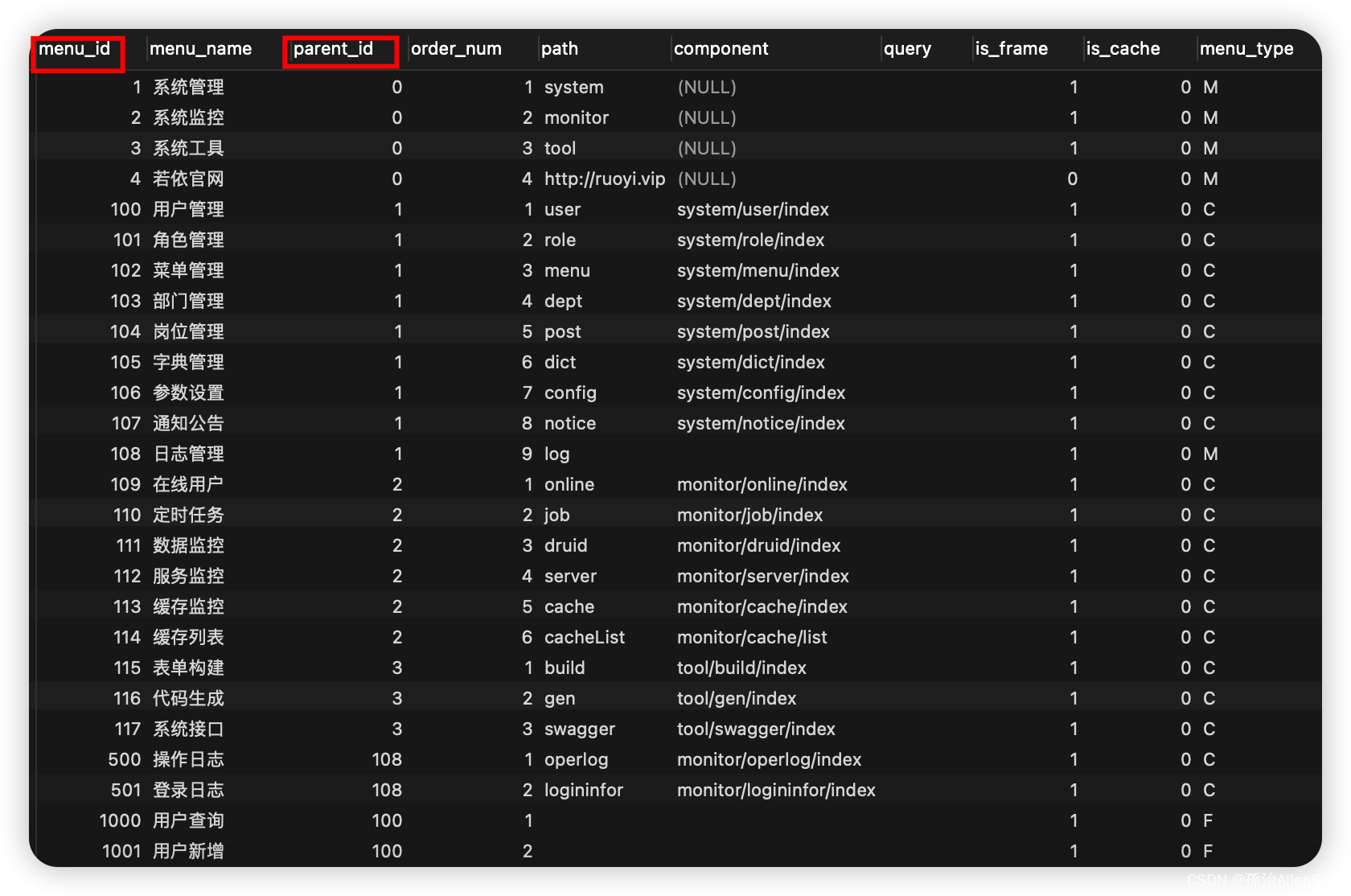
后端代码实现

public static void main(String[] args) {
        Node[] nodes = new Node[]{
            new Node(1, 0, "123"),
            new Node(2, 1, "1234"),
            new Node(3, 1, "1235"),
            new Node(4, 3, "1236"),
            new Node(5, 2, "1237"),
        };
        print(Arrays.asList(nodes));
    }
    
    public static void print(List<Node> list) {
        // 节点信息映射
        Map<Integer, Node> nodeInfoMap = new HashMap<>();
        // 每个父节点对应的子节点列表
        Map<Integer, List<Integer>> childrenIdMap = new HashMap<>();
        List<Node> curLevelNodes = new ArrayList<>();
        for (Node node : list) {
            nodeInfoMap.put(node.id, node);
            if (node.parentId == 0) {
                curLevelNodes.add(node);
            } else {
                List<Integer> children = childrenIdMap.get(node.parentId);
                if (children == null) {
                    children = new ArrayList<>();
                    childrenIdMap.put(node.parentId, children);
                }
                children.add(node.id);
            }
        }
        for (Node node : curLevelNodes) {
            printRecursively(nodeInfoMap, childrenIdMap, node, "");
        }
    }
    
    private static void printRecursively(Map<Integer, Node> nodeInfoMap,
                                  Map<Integer, List<Integer>> childrenIdMap,
                                  Node node, String prefix) {
        System.out.println(prefix + node.name);
        List<Integer> children = childrenIdMap.get(node.id);
        if (children != null) {
            for (Integer childId : children) {
                printRecursively(nodeInfoMap, childrenIdMap, nodeInfoMap.get(childId), prefix + " ");
            }
        }
    }
    
    @AllArgsConstructor
    private static class Node {
        int id;
        int parentId;
        String name;
    }

【三】方式二：子集

（1）方法介绍

也称为Closure table或Bridge table，该方法将树表示为嵌套的子集：根节点包含所有深度为1的节点，它们依次包含深度为2的节点，依此类推

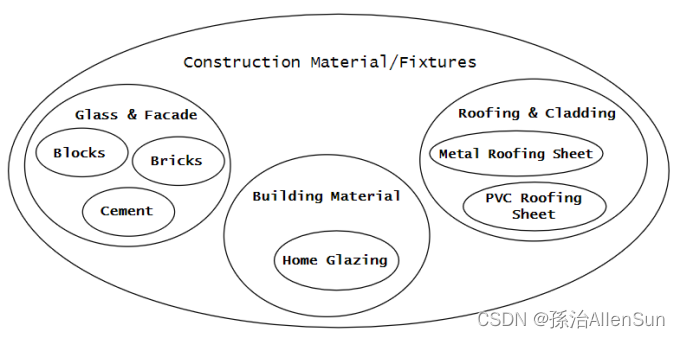
Subsets方法需要两个表：第一个表包含所有子集（表goods_category，图4），第二个表包含子集的包含事实，以及相应的深度级别（表subset，图4）。

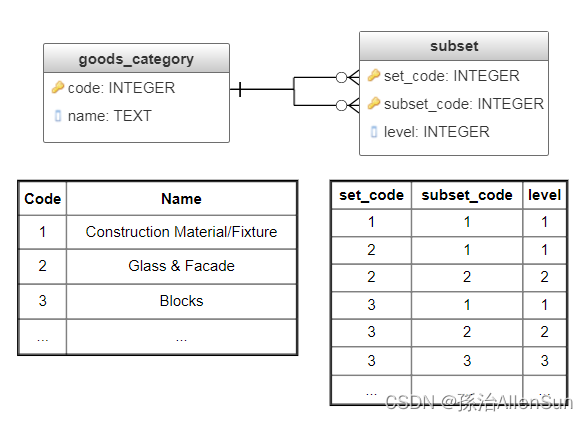
结果，对于树中的每个节点，该subset表包含的记录数等于该节点的深度级别。因此，记录数随着算术级数的增长而增加，但是普通查询变得比以前的方法更简单，更快。

（1）获取给定节点的子树：

SELECT name, set_code, subset_code, level FROM subset s
    LEFT JOIN goods_category c ON c.code = s.set_code
WHERE subset_code = 1 /* the subtree root */
ORDER BY level;

（2）从根到给定节点的路径：

SELECT name, set_code, subset_code, level FROM subset s
    LEFT JOIN goods_category c ON c.code = s.subset_code
WHERE set_code = 3 /* the give node */
ORDER BY level;

（3）检查“块”节点（代码= 3）是否为“建筑材料/夹具”（代码= 1）的后代：

SELECT CASE 
    WHEN exists(SELECT 1 FROM subset 
                WHERE set_code = 3 AND subset_code = 1)
	THEN 'true' 
	ELSE 'false' 
	END

为了保持完整性，移动和插入操作需要实现触发器，该触发器将更新所有关联的记录。

（2）优点

Subsets方法的主要优点\是支持快速，简单，非递归的树操作：子树选择，祖先选择，节点深度级别的计算和后代数量。

（3）缺点

（1）相对不直观的数据表示（由于间接后代之间的冗余引用而变得复杂）；
（2）数据冗余；
（3）数据完整性需要触发器；
（4）移动和插入操作比邻接列表方法更为复杂。插入需要为每个后代节点附加记录，而移动节点需要更新其后代和祖先的记录。

【四】方式三：嵌套集

（1）方法介绍

此方法的思想是存储树的前缀遍历。在此首先访问树的根，然后按前缀顺序访问左子树的所有节点，然后再次按前缀顺序访问右子树的节点。遍历的顺序存储在两个附加字段中：left_key和right_key。该left_key字段包含进入子树之前的遍历步骤数，而right_key包含离开子树之前的遍历步骤数。结果，对于每个节点，其后代的节点号在节点号之间，而与它们的深度级别无关。此属性允许编写查询而无需采用递归。

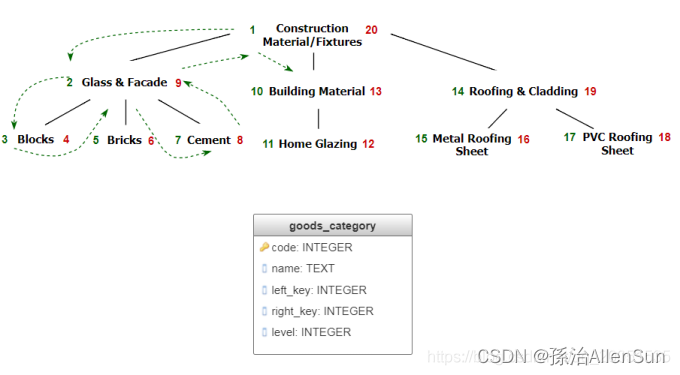
（1）获取给定节点的子树：

WITH root AS (SELECT left_key, right_key FROM goods_category WHERE code=2 /* id of the node */)
SELECT * FROM goods_category
    WHERE left_key >= (SELECT left_key FROM root) 
        AND right_key <= (SELECT right_key FROM root)
ORDER BY level;

（2）从根到给定节点的路径：

WITH node AS (SELECT left_key, right_key FROM goods_category WHERE code=8 /* id of the node */)
SELECT * FROM goods_category
    WHERE left_key <= (SELECT left_key FROM node) 
        AND right_key >= (SELECT right_key FROM node)
ORDER BY level;

（3）检查“块”节点是否是“建筑材料/夹具”节点的后代：

SELECT CASE 
    WHEN exists(SELECT 1 from goods_category AS gc1, goods_category gc2 
        WHERE gc1.code = 1 
            AND gc2.code = 3 
            AND gc1.left_key <= gc2.left_key 
            AND gc1.right_key >= gc2.right_key)
    THEN 'true'
    ELSE 'false'
END

（2）优点

它允许快速而简单的操作来选择节点的祖先，后代，其计数和深度级别，而无需递归。

（3）缺点

在插入或移动节点时必须重新分配遍历顺序。例如，为了将一个节点添加到最底层，有必要将所有节点的left_keyandright_key字段更新为其“ right and above”，这可能需要重新遍历整个树。可以通过分配给减少更新的数量left_key和right_key具有间隔，例如值10 000和200 000代替的1和20。这将允许插入节点而无需对其他节点重新编号。另一种方法是对left_key和的值使用实数right_key。

【五】方式四：物化路径

（1）方法介绍

也称为沿袭列，此方法的想法是显式存储从根开始的整个路径作为节点的主键（图6）。物化路径是表示树的一种优雅方式：每个节点都有一个直观的标识符，其中的各个部分都有明确定义的语义。此属性对于通用分类非常重要，包括国际疾病分类（ICD），科学论文中使用的通用小数分类（UDC），PACS（物理和天文学分类方案）。此方法的查询很简洁，但并不总是有效的，因为它们涉及子字符串匹配。

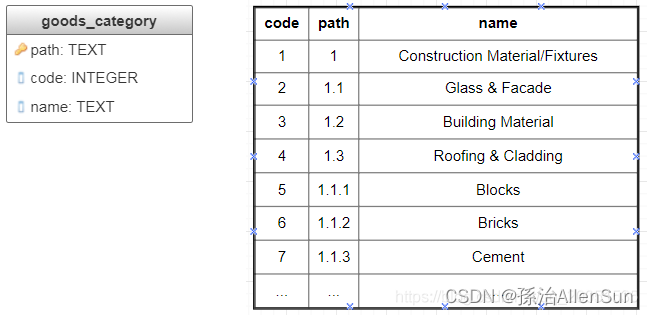
（1）获取给定节点的子树：

SELECT * FROM goods_category WHERE path LIKE '1.1%' ORDER BY path

（2）从根到给定节点的路径：

SELECT * FROM goods_category WHERE '1.1.3' LIKE path||'%' ORDER BY path

（3）检查“水泥”节点是否为“建筑材料/夹具”节点的后代：

SELECT CASE 
    WHEN exists(SELECT 1 FROM goods_category AS gc1, goods_category AS gc2
        WHERE gc1.name = 'Construction Material/Fixtures' 	
            AND gc2.name = 'Cement' 
            AND gc2.path LIKE gc1.path||'%')
    THEN 'true'
    ELSE 'false'
END

对于事先知道级别数和每个级别上的节点数的情况，可以通过使用带有严格定义的零填充小数位组的数字标识符来避免使用显式分隔符。这种方法被用于许多分类中，包括OKATO，NAICS。

也可以将单独的列用于层次结构的各个级别（多个谱系列）：这将消除使用子字符串匹配的必要性。

物化路径方法的优点是数据的直观表示以及某些常见查询的简单性。

该方法的缺点包括复杂的插入，移动和删除操作，完整性约束的简单实现以及由于需要进行子字符串匹配而导致的查询效率低下。在使用数字标识符方法的情况下，另一个可能的缺点是深度级别的数量有限。