机器学习笔记之优化算法——梯度下降法:凸函数VS强凸函数
- 引言
- 凸函数:
- 凸函数的定义与判定条件
- 凸函数的一阶条件
- 凸函数的梯度单调性
- 凸函数的二阶条件
- 强凸函数
- 强凸函数的定义
- 强凸函数的判定条件
- 强凸函数的一阶条件
- 强凸函数的梯度单调性
- 强突函数的二阶条件
引言
本节将介绍凸函数、强凸函数以及它们之间的联系(补梯度下降法:总体介绍中的坑)。
凸函数:
凸函数的定义与判定条件
关于凸函数的定义表示如下:设
f
(
⋅
)
f(\cdot)
f(⋅)为定义在空间
I
\mathcal I
I上的函数,若对
I
\mathcal I
I上的任意两点
x
1
,
x
2
x_1,x_2
x1,x2与任意实数
λ
∈
(
0
,
1
)
\lambda \in (0,1)
λ∈(0,1)总有:
通常将空间
I
\mathcal I
I设置为实数域与空间
⇒
R
n
\Rightarrow \mathbb R^n
⇒Rn。
f
[
λ
⋅
x
2
+
(
1
−
λ
)
⋅
x
1
]
≤
λ
⋅
f
(
x
2
)
+
(
1
−
λ
)
⋅
f
(
x
1
)
f[\lambda \cdot x_2 + (1 - \lambda) \cdot x_1] \leq \lambda \cdot f(x_2) + (1 - \lambda) \cdot f(x_1)
f[λ⋅x2+(1−λ)⋅x1]≤λ⋅f(x2)+(1−λ)⋅f(x1)
则称:函数
f
(
⋅
)
f(\cdot)
f(⋅)为
I
\mathcal I
I上的凸函数。对应示例图像表示如下:
将其转化:
λ
⋅
x
2
+
(
1
−
λ
)
⋅
x
1
=
x
1
+
λ
⋅
(
x
2
−
x
1
)
\lambda \cdot x_2 + (1 - \lambda)\cdot x_1 = x_1 + \lambda \cdot (x_2 - x_1)
λ⋅x2+(1−λ)⋅x1=x1+λ⋅(x2−x1),那么
λ
(
x
2
−
x
1
)
\lambda(x_2 - x_1)
λ(x2−x1)可看作增量,而
λ
\lambda
λ可看作控制增量的参数。

凸函数的一种判定条件:构造一个函数
G
(
t
)
\mathcal G(t)
G(t),满足:
G
(
t
)
≜
f
(
x
+
v
⋅
t
)
∀
x
,
v
∈
R
n
,
t
∈
R
\mathcal G(t) \triangleq f(x + v \cdot t) \quad \forall x,v \in \mathbb R^n,t \in \mathbb R
G(t)≜f(x+v⋅t)∀x,v∈Rn,t∈R
则有推论:
f
(
⋅
)
f(\cdot)
f(⋅)是凸函数
⇔
G
(
t
)
\Leftrightarrow \mathcal G(t)
⇔G(t)是凸函数。在一般情况下,我们面对的权重空间是一个高维空间,而在高维空间中的目标函数
f
(
⋅
)
f(\cdot)
f(⋅)也通常是一个高维函数。假设:权重空间是一个
2
2
2维空间,对应的目标函数
f
(
⋅
)
f(\cdot)
f(⋅)也是一个
2
2
2维函数:
即:输入变量的维度是
2
2
2维,而目标函数的输出结果是
1
1
1维标量。
f
(
⋅
)
:
R
2
↦
R
f(\cdot):\mathbb R^2 \mapsto \mathbb R
f(⋅):R2↦R
那么如何验证
f
(
⋅
)
f(\cdot)
f(⋅)描述的图像在高维空间中的曲面是否为凸的
?
?
?在介绍方向导数中提到:关于某一点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)关于函数
f
(
⋅
)
f(\cdot)
f(⋅)在方向
l
⃗
\vec l
l的方向导数
∂
Z
∂
l
⃗
∣
(
x
0
,
y
0
)
\begin{aligned}\frac{\partial \mathcal Z}{\partial \vec l}|_{(x_0,y_0)}\end{aligned}
∂l∂Z∣(x0,y0)表示为下图中在
l
⃗
\vec l
l方向上过
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)做一个垂直于
X
O
Y
\mathcal X\mathcal O\mathcal Y
XOY的平面,平面与
f
(
⋅
)
f(\cdot)
f(⋅)相交的图像在
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)处的斜率结果:
其中黄色菱形部分表示垂直于X O Y \mathcal X\mathcal O\mathcal Y XOY平面在l ⃗ \vec l l方向上并过( x 0 , y 0 ) (x_0,y_0) (x0,y0)黄色点的平面;红色点则表示( x 0 , y 0 ) (x_0,y_0) (x0,y0)在函数f ( ⋅ ) f(\cdot) f(⋅)上的结果;而黑色实线则表示过映射点与函数图像相切的直线,其斜率即方向导数∂ Z ∂ l ⃗ ∣ ( x 0 , y 0 ) \begin{aligned}\frac{\partial \mathcal Z}{\partial \vec l}|_{(x_0,y_0)}\end{aligned} ∂l∂Z∣(x0,y0)。

但这里我们并不关注方向导数,而是关注平面与函数图像之间相交所产生的截线的形状。可以观察上述图像对应的俯视图结果:
无论是上图还是俯视图,都没有对
f
(
x
,
y
)
f(x,y)
f(x,y)进行完全表示,这仅仅是其中一部分图像。

从俯视图角度可以看到:黄色截面简化成了一条直线。这实际上可看做上述判定条件中函数
x
+
v
⋅
t
x+v \cdot t
x+v⋅t的某一种结果。而对应的
f
(
x
+
v
⋅
t
)
f(x + v \cdot t)
f(x+v⋅t)则表达:截面与函数图像之间相交产生的截线。
如果从向量的角度认识,以下面红色直线为例:

其中
x
,
v
x,v
x,v是任意
R
n
\mathbb R^n
Rn的向量,从而
x
+
v
⋅
t
x+v \cdot t
x+v⋅t可表示为该图黑色虚线的结果。由于
t
∈
R
t \in \mathbb R
t∈R,如果我们将所有的
t
t
t全部取到,那么最终构成
x
+
v
⋅
t
x + v \cdot t
x+v⋅t构成向量的集合就是红色直线的结果。
关于向量v v v,我们通常将其视作单位向量。因为即便不是单位向量,在转化为单位向量过程中得到的标量系数k k k也可以与t t t进行合并:t ∈ R ⇒ k ⋅ t ∈ R t \in\mathbb R \Rightarrow k \cdot t \in \mathbb R t∈R⇒k⋅t∈R。如果将v v v看作单位向量e ⃗ ( cos α , cos β ) \vec e(\cos \alpha,\cos\beta) e(cosα,cosβ),那么过点P ( x 0 , y 0 ) \mathcal P(x_0,y_0) P(x0,y0),并且方向与e ⃗ \vec e e平行的直线参数方程可表示为:
Y = ( x 0 , y 0 ) + t ⋅ e ⃗ = ( x 0 , y 0 ) + t ⋅ ( cos α , cos β ) \mathcal Y = (x_0,y_0) + t \cdot \vec e = (x_0,y_0) + t \cdot (\cos\alpha,\cos\beta) Y=(x0,y0)+t⋅e=(x0,y0)+t⋅(cosα,cosβ)
因此,关于该判定条件的另一种表达有:如果
x
+
v
⋅
t
x + v \cdot t
x+v⋅t在该权重空间中描述的任意一个截面,其与函数
f
(
⋅
)
f(\cdot)
f(⋅)相交产生的任意一条截线对应的函数均是凸函数,那么函数
f
(
⋅
)
f(\cdot)
f(⋅)也是一个凸函数,反之同理。
这是一个充分必要条件。
凸函数的一阶条件
在函数
f
(
⋅
)
f(\cdot)
f(⋅)可微的条件下,有:
相比于上述的定义与判定条件,并没有要求函数
f
(
⋅
)
f(\cdot)
f(⋅)一定是可微的。也就是说:一个函数是凸函数,并不要求该函数一定可微。
f
(
⋅
)
is Convex
⇔
f
(
x
2
)
≥
f
(
x
1
)
+
[
∇
f
(
x
1
)
]
T
⋅
(
x
2
−
x
1
)
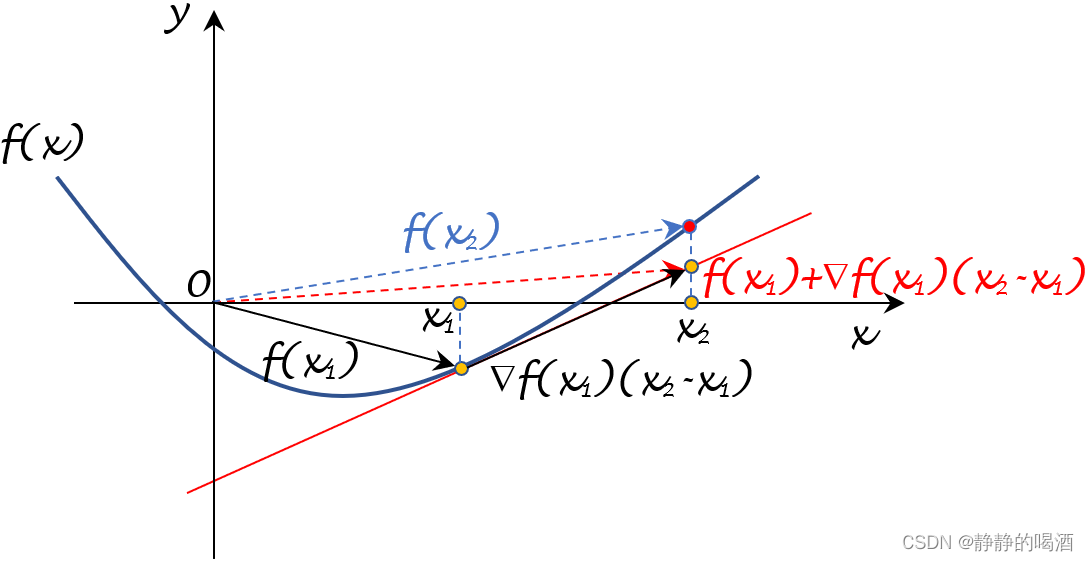
f(\cdot) \text{ is Convex} \Leftrightarrow f(x_2) \geq f(x_1) + [\nabla f(x_1)]^T \cdot (x_2-x_1)
f(⋅) is Convex⇔f(x2)≥f(x1)+[∇f(x1)]T⋅(x2−x1)
这是一个充分必要条件。可以在图像中看到这个现象:
(
2023/8/10
)
(\text{2023/8/10})
(2023/8/10)补充
证明:充分性
- 要证: f [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] ≤ λ ⋅ f ( x 1 ) + ( 1 − λ ) ⋅ f ( x 2 ) , ∀ x 1 , x 2 ∈ C , λ ∈ ( 0 , 1 ) f[\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] \leq \lambda \cdot f(x_1) + (1 - \lambda) \cdot f(x_2),\forall x_1,x_2 \in \mathcal C,\lambda \in (0,1) f[λ⋅x1+(1−λ)⋅x2]≤λ⋅f(x1)+(1−λ)⋅f(x2),∀x1,x2∈C,λ∈(0,1)
- 将
λ
⋅
x
1
+
(
1
−
λ
)
⋅
x
2
\lambda \cdot x_1 + (1 - \lambda) \cdot x_2
λ⋅x1+(1−λ)⋅x2记作
Z
\mathcal Z
Z,从而有:
Z
∈
C
\mathcal Z \in \mathcal C
Z∈C。既然
Z
\mathcal Z
Z同样是定义域
C
\mathcal C
C上一点,根据假设条件必然有:
{ f ( x 1 ) ≥ f ( Z ) + [ ∇ f ( Z ) ] T ⋅ ( x 1 − Z ) f ( x 2 ) ≥ f ( Z ) + [ ∇ f ( Z ) ] T ⋅ ( x 2 − Z ) \begin{cases} f(x_1) & \geq f(\mathcal Z) + [\nabla f(\mathcal Z)]^T \cdot (x_1 - \mathcal Z) \\ f(x_2) & \geq f(\mathcal Z) + [\nabla f(\mathcal Z)]^T \cdot (x_2 - \mathcal Z)\end{cases} {f(x1)f(x2)≥f(Z)+[∇f(Z)]T⋅(x1−Z)≥f(Z)+[∇f(Z)]T⋅(x2−Z) - 将上述两个不等式的左右两端分别乘以
λ
,
1
−
λ
\lambda,1 - \lambda
λ,1−λ。由于
λ
∈
(
0
,
1
)
\lambda \in (0,1)
λ∈(0,1),因而不等式符号不发生变化:
{ λ ⋅ f ( x 1 ) ≥ λ ⋅ f ( Z ) + λ [ ∇ f ( Z ) ] T ⋅ ( x 1 − Z ) ( 1 − λ ) ⋅ f ( x 2 ) ≥ ( 1 − λ ) ⋅ f ( Z ) + ( 1 − λ ) ⋅ [ ∇ f ( Z ) ] T ⋅ ( x 2 − Z ) \begin{cases} \begin{aligned} \lambda \cdot f(x_1) & \geq \lambda \cdot f(\mathcal Z) + \lambda [\nabla f(\mathcal Z)]^T \cdot (x_1 - \mathcal Z) \\ (1 - \lambda) \cdot f(x_2) & \geq (1 - \lambda) \cdot f(\mathcal Z) + (1 - \lambda) \cdot [\nabla f(\mathcal Z)]^T \cdot (x_2 - \mathcal Z) \end{aligned} \end{cases} {λ⋅f(x1)(1−λ)⋅f(x2)≥λ⋅f(Z)+λ[∇f(Z)]T⋅(x1−Z)≥(1−λ)⋅f(Z)+(1−λ)⋅[∇f(Z)]T⋅(x2−Z)
将上述两不等式对应位置相加,有:
λ f ( x 1 ) + ( 1 − λ ) ⋅ f ( x 2 ) ≥ ( λ + 1 − λ ) ⋅ f ( Z ) + [ ∇ f ( Z ) ] T ⋅ [ ( λ ⋅ x 1 − λ ⋅ Z ) + ( 1 − λ ) ⋅ x 2 − ( 1 − λ ) ⋅ Z ] ≥ f ( Z ) + [ ∇ f ( Z ) ] T ⋅ [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 − Z ] \begin{aligned} \lambda f(x_1) + (1 - \lambda) \cdot f(x_2) & \geq (\lambda + 1 - \lambda) \cdot f(\mathcal Z) + [\nabla f(\mathcal Z)]^T \cdot [(\lambda \cdot x_1 - \lambda \cdot \mathcal Z) + (1 - \lambda) \cdot x_2 - (1 - \lambda) \cdot \mathcal Z] \\ & \geq f(\mathcal Z) + [\nabla f(\mathcal Z)]^T \cdot [\lambda \cdot x_1 + (1 - \lambda) \cdot x_2 - \mathcal Z] \end{aligned} λf(x1)+(1−λ)⋅f(x2)≥(λ+1−λ)⋅f(Z)+[∇f(Z)]T⋅[(λ⋅x1−λ⋅Z)+(1−λ)⋅x2−(1−λ)⋅Z]≥f(Z)+[∇f(Z)]T⋅[λ⋅x1+(1−λ)⋅x2−Z]
由于: λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 \lambda \cdot x_1 + (1 - \lambda) \cdot x_2 λ⋅x1+(1−λ)⋅x2记作 Z \mathcal Z Z,因此后一项: [ ∇ f ( Z ) ] T ⋅ [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 − Z ] = 0 [\nabla f(\mathcal Z)]^T \cdot [\lambda \cdot x_1 + (1 - \lambda) \cdot x_2 - \mathcal Z] = 0 [∇f(Z)]T⋅[λ⋅x1+(1−λ)⋅x2−Z]=0。最后将 Z \mathcal Z Z带入,整理有:
这正是凸函数的定义。
λ f ( x 1 ) + ( 1 − λ ) ⋅ f ( x 2 ) ≥ f ( Z ) = f [ λ ⋅ x 1 + ( 1 − λ ) ⋅ x 2 ] \lambda f(x_1) + (1 - \lambda) \cdot f(x_2) \geq f(\mathcal Z) = f[\lambda \cdot x_1 + (1 - \lambda) \cdot x_2] λf(x1)+(1−λ)⋅f(x2)≥f(Z)=f[λ⋅x1+(1−λ)⋅x2]
证明:必要性
-
在已知 f ( ⋅ ) f(\cdot) f(⋅)是凸函数的条件下:
即便将x 1 , x 2 x_1,x_2 x1,x2调换位置,也不会影响公式的成立。
f [ λ ⋅ x 2 + ( 1 − λ ) ⋅ x 1 ] ≤ λ ⋅ f ( x 2 ) + ( 1 − λ ) ⋅ f ( x 1 ) x 1 , x 2 ∈ C ; λ ∈ ( 0 , 1 ) f [\lambda \cdot x_2 + (1 - \lambda) \cdot x_1] \leq \lambda \cdot f(x_2) + (1 - \lambda) \cdot f(x_1) \quad x_1,x_2 \in \mathcal C;\lambda \in (0,1) f[λ⋅x2+(1−λ)⋅x1]≤λ⋅f(x2)+(1−λ)⋅f(x1)x1,x2∈C;λ∈(0,1)- 观察不等式左侧,有:
f [ λ ⋅ x 2 + ( 1 − λ ) ⋅ x 1 ] = f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] f[\lambda \cdot x_2 + (1 - \lambda) \cdot x_1] = f [x_1 + \lambda \cdot (x_2 - x_1)] f[λ⋅x2+(1−λ)⋅x1]=f[x1+λ⋅(x2−x1)] - 观察不等式右侧,有:
λ ⋅ f ( x 2 ) + ( 1 − λ ) ⋅ f ( x 1 ) = f ( x 1 ) + λ ⋅ [ f ( x 2 ) − f ( x 1 ) ] \lambda \cdot f(x_2) + (1 - \lambda) \cdot f(x_1) = f(x_1) + \lambda \cdot [f(x_2) - f(x_1)] λ⋅f(x2)+(1−λ)⋅f(x1)=f(x1)+λ⋅[f(x2)−f(x1)]
最终将上式整理得:
将f ( x 2 ) f(x_2) f(x2)以外的其他项移到不等号左侧,不等号不发生变化。
f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] − f ( x 1 ) λ + f ( x 1 ) ≤ f ( x 2 ) \frac{f [x_1 + \lambda \cdot (x_2 - x_1)] - f(x_1)}{\lambda} + f(x_1)\leq f(x_2) λf[x1+λ⋅(x2−x1)]−f(x1)+f(x1)≤f(x2) - 观察不等式左侧,有:
-
对项 f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] f [x_1 + \lambda \cdot (x_2 - x_1)] f[x1+λ⋅(x2−x1)]关于 x 1 x_1 x1进行泰勒展开:
其中O ( ⋅ ) \mathcal O(\cdot) O(⋅)表示高阶无穷小。
f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] = f ( x 1 ) + 1 1 ! λ ⋅ [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) + O ( λ ⋅ ∣ ∣ x 2 − x 1 ∣ ∣ ) \begin{aligned} f[x_1 + \lambda \cdot (x_2 - x_1)] = f(x_1) + \frac{1}{1!}\lambda \cdot [\nabla f(x_1)]^T (x_2 - x_1) + \mathcal O(\lambda \cdot ||x_2 - x_1||) \end{aligned} f[x1+λ⋅(x2−x1)]=f(x1)+1!1λ⋅[∇f(x1)]T(x2−x1)+O(λ⋅∣∣x2−x1∣∣)
将上式的 f ( x 1 ) f(x_1) f(x1)移至等号左侧,并将等式左右两侧同时除以 λ \lambda λ,有:
f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] − f ( x 1 ) λ = [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) + O ( λ ⋅ ∣ ∣ x 2 − x 1 ∣ ∣ ) λ \frac{f[x_1 + \lambda \cdot (x_2 - x_1)] - f(x_1)}{\lambda} = [\nabla f(x_1)]^T (x_2 - x_1) + \frac{\mathcal O(\lambda \cdot ||x_2 - x_1||)}{\lambda} λf[x1+λ⋅(x2−x1)]−f(x1)=[∇f(x1)]T(x2−x1)+λO(λ⋅∣∣x2−x1∣∣)
由于 λ ∈ ( 0 , 1 ) \lambda \in (0,1) λ∈(0,1),因此这里令 λ ⇒ 0 \lambda \Rightarrow 0 λ⇒0,有:
关于lim λ ⇒ 0 O ( λ ⋅ ∣ ∣ x 2 − x 1 ∣ ∣ ) λ \begin{aligned}\mathop{\lim}\limits_{\lambda \Rightarrow 0} \frac{\mathcal O(\lambda \cdot ||x_2 - x_1||)}{\lambda}\end{aligned} λ⇒0limλO(λ⋅∣∣x2−x1∣∣),其中分子是关于λ \lambda λ的高阶无穷小,而分子仅是一阶。因此该项分子趋近0 0 0的速度要快于分母,从而为0 0 0。
f [ x 1 + λ ⋅ ( x 2 − x 1 ) ] − f ( x 1 ) λ = [ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) \frac{f[x_1 + \lambda \cdot (x_2 - x_1)] - f(x_1)}{\lambda} = [\nabla f(x_1)]^T (x_2 - x_1) λf[x1+λ⋅(x2−x1)]−f(x1)=[∇f(x1)]T(x2−x1) -
将该式带入到上述步骤,有:
[ ∇ f ( x 1 ) ] T ( x 2 − x 1 ) + f ( x 1 ) ≤ f ( x 2 ) [\nabla f(x_1)]^T (x_2 - x_1) + f(x_1) \leq f(x_2) [∇f(x1)]T(x2−x1)+f(x1)≤f(x2)
凸函数的梯度单调性
在函数
f
(
⋅
)
f(\cdot)
f(⋅)可微的条件下,
[
∇
f
(
x
)
−
∇
f
(
y
)
]
[\nabla f(x) - \nabla f(y)]
[∇f(x)−∇f(y)]与
x
−
y
x-y
x−y之间同号。即:
f
(
⋅
)
is Convex
⇔
[
∇
f
(
x
)
−
∇
f
(
y
)
]
T
(
x
−
y
)
≥
0
f(\cdot) \text{ is Convex } \Leftrightarrow [\nabla f(x) - \nabla f(y)]^T (x - y) \geq 0
f(⋅) is Convex ⇔[∇f(x)−∇f(y)]T(x−y)≥0
证明:必要性
如果
f
(
⋅
)
f(\cdot)
f(⋅)是可微的凸函数,根据凸函数的一阶条件,有:
{
f
(
y
)
≥
f
(
x
)
+
[
∇
f
(
x
)
]
T
⋅
(
y
−
x
)
f
(
x
)
≥
f
(
y
)
+
[
∇
f
(
y
)
]
T
⋅
(
x
−
y
)
\begin{cases} \begin{aligned} f(y) \geq f(x) + [\nabla f(x)]^T \cdot (y - x) \\ f(x) \geq f(y) + [\nabla f(y)]^T \cdot (x - y) \end{aligned} \end{cases}
{f(y)≥f(x)+[∇f(x)]T⋅(y−x)f(x)≥f(y)+[∇f(y)]T⋅(x−y)
将上述式子相加,有:
[
∇
f
(
x
)
−
∇
f
(
y
)
]
T
⋅
(
x
−
y
)
≥
0
[\nabla f(x) - \nabla f(y)]^T \cdot (x - y) \geq 0
[∇f(x)−∇f(y)]T⋅(x−y)≥0
证明:充分性
如果
f
(
⋅
)
f(\cdot)
f(⋅)的梯度
∇
f
(
⋅
)
\nabla f(\cdot)
∇f(⋅)是单调的,定义关于
t
∈
[
0
,
1
]
t \in [0,1]
t∈[0,1]的函数
G
(
t
)
\mathcal G(t)
G(t):
G
(
t
)
=
f
[
x
+
t
⋅
(
y
−
x
)
]
\mathcal G(t) = f[x + t \cdot (y - x)]
G(t)=f[x+t⋅(y−x)]
对应
G
(
t
)
\mathcal G(t)
G(t)的导数
G
′
(
t
)
\mathcal G'(t)
G′(t):
G
′
(
t
)
=
[
∇
f
(
x
+
t
⋅
(
y
−
x
)
)
]
T
⋅
(
y
−
x
)
\mathcal G'(t) = [\nabla f(x + t \cdot (y-x))]^T \cdot (y-x)
G′(t)=[∇f(x+t⋅(y−x))]T⋅(y−x)
由于
G
′
(
t
)
\mathcal G'(t)
G′(t)在
t
∈
[
0
,
1
]
t \in [0,1]
t∈[0,1]上连续,且:
[
∇
f
(
x
)
−
∇
f
(
y
)
]
T
⋅
(
x
−
y
)
≥
0
[\nabla f(x) - \nabla f(y)]^T \cdot (x - y) \geq 0
[∇f(x)−∇f(y)]T⋅(x−y)≥0
从而有:
消了两个负号~
G
′
(
t
)
≥
G
′
(
0
)
⇐
{
G
′
(
1
)
−
G
′
(
0
)
=
[
∇
f
(
y
)
−
∇
f
(
x
)
]
T
⋅
(
y
−
x
)
≥
0
G
′
(
0
)
−
G
′
(
0
)
=
0
\mathcal G'(t) \geq \mathcal G'(0) \Leftarrow \begin{cases} \mathcal G'(1) - \mathcal G'(0) = [\nabla f(y) - \nabla f(x)]^T \cdot (y-x) \geq 0 \\ \mathcal G'(0) - \mathcal G'(0) = 0 \end{cases}
G′(t)≥G′(0)⇐{G′(1)−G′(0)=[∇f(y)−∇f(x)]T⋅(y−x)≥0G′(0)−G′(0)=0
最终有:
f
(
y
)
=
G
(
1
)
=
G
(
0
)
+
∫
0
1
G
′
(
t
)
d
t
≥
G
(
0
)
+
G
′
(
0
)
=
f
(
x
)
+
[
∇
f
(
x
)
]
T
(
y
−
x
)
f(y) = \mathcal G(1) = \mathcal G(0) + \int_0^1 \mathcal G'(t) dt \geq \mathcal G(0) + \mathcal G'(0) = f(x) + [\nabla f(x)]^T (y-x)
f(y)=G(1)=G(0)+∫01G′(t)dt≥G(0)+G′(0)=f(x)+[∇f(x)]T(y−x)
即:
f
(
⋅
)
f(\cdot)
f(⋅)为凸函数。
凸函数的二阶条件
在函数
f
(
⋅
)
f(\cdot)
f(⋅)二阶可微的条件下,说明关于
f
(
⋅
)
f(\cdot)
f(⋅)的二阶梯度
∇
2
f
(
⋅
)
\nabla^2 f(\cdot)
∇2f(⋅)存在,即对应的
Hessian Matrix
\text{Hessian Matrix}
Hessian Matrix存在。从而有该矩阵是一个半正定矩阵:
简单注意一下,这里的
0
0
0指的是
0
0
0矩阵。
f
(
⋅
)
is Convex
⇔
∇
2
f
(
x
)
≽
0
f(\cdot) \text{ is Convex } \Leftrightarrow \nabla^2 f(x) \succcurlyeq 0
f(⋅) is Convex ⇔∇2f(x)≽0
(
2023
/
8
/
10
)
(2023/8/10)
(2023/8/10)补充
证明:充分性
已知
Hessian Matrix
\text{Hessian Matrix}
Hessian Matrix是半正定矩阵
(
∇
2
f
(
x
)
≽
0
,
∀
x
∈
C
)
(\nabla^2 f(x) \succcurlyeq 0,\forall x \in \mathcal C)
(∇2f(x)≽0,∀x∈C):
- 基于
y
∈
C
y \in \mathcal C
y∈C,针对
f
(
y
)
f(y)
f(y)关于某点
x
x
x进行泰勒展开:
其中ξ \xi ξ表示( x , y ) (x,y) (x,y)范围内的一点,标准表示:ξ = x + λ ⋅ ( y − x ) ; λ ∈ ( 0 , 1 ) \xi = x + \lambda \cdot (y - x);\lambda \in (0,1) ξ=x+λ⋅(y−x);λ∈(0,1)不否认ξ ∈ C \xi \in \mathcal C ξ∈C。
f ( y ) = f ( x ) + 1 1 ! [ ∇ f ( x ) ] T ( y − x ) + 1 2 ! ( y − x ) T [ ∇ 2 f ( ξ ) ] ( y − x ) + O ( ⋅ ) f(y) = f(x) + \frac{1}{1!}[\nabla f(x)]^T (y - x) + \frac{1}{2!} (y -x)^T [\nabla^2 f(\xi)](y -x) + \mathcal O(\cdot) f(y)=f(x)+1!1[∇f(x)]T(y−x)+2!1(y−x)T[∇2f(ξ)](y−x)+O(⋅)
- 由于
∇
2
f
(
ξ
)
≽
0
\nabla^2 f(\xi) \succcurlyeq 0
∇2f(ξ)≽0,必然有:
f ( y ) ≥ f ( x ) + [ ∇ f ( x ) ] T ( y − x ) f(y) \geq f(x) + [\nabla f(x)]^T (y-x) f(y)≥f(x)+[∇f(x)]T(y−x) - 根据上述凸函数的一阶条件,自然得证: f ( ⋅ ) f(\cdot) f(⋅)是凸函数。
证明:必要性
已知
f
(
⋅
)
f(\cdot)
f(⋅)是凸函数,要证:
∇
2
f
(
x
)
≽
0
,
∀
x
∈
C
\nabla^2 f(x) \succcurlyeq 0,\forall x \in \mathcal C
∇2f(x)≽0,∀x∈C。
- 从定义域
C
\mathcal C
C中任取一点
x
x
x,观察:从
x
x
x开始,沿着
d
d
d方向移动了较小步长
α
\alpha
α后位置的函数结果
f
(
x
+
α
⋅
d
)
f(x + \alpha \cdot d)
f(x+α⋅d),并针对该结果关于
x
x
x进行泰勒展开:
其中x + α ⋅ d ∈ C x + \alpha \cdot d \in \mathcal C x+α⋅d∈C。
f ( x + α ⋅ d ) = f ( x ) + 1 1 ! α ⋅ [ ∇ f ( x ) ] T d ⏟ 一阶条件 + 1 2 ! α 2 ⋅ d T [ ∇ 2 f ( x ) ] ⋅ d + O ( α 2 ⋅ ∣ ∣ d ∣ ∣ 2 ) f(x + \alpha \cdot d) = \underbrace{f(x) + \frac{1}{1!} \alpha \cdot [\nabla f(x)]^T d}_{一阶条件} + \frac{1}{2!} \alpha^2 \cdot d^T [\nabla^2 f(x)] \cdot d + \mathcal O(\alpha^2 \cdot ||d||^2) f(x+α⋅d)=一阶条件 f(x)+1!1α⋅[∇f(x)]Td+2!1α2⋅dT[∇2f(x)]⋅d+O(α2⋅∣∣d∣∣2) - 根据凸函数的一阶条件,必然有:
这依然依赖移动后的结果依然∈ C \in \mathcal C ∈C。
f ( x + α ⋅ d ) ≥ f ( x ) + α ⋅ [ ∇ f ( x ) ] T d f(x + \alpha \cdot d) \geq f(x) + \alpha \cdot [\nabla f(x)]^T d f(x+α⋅d)≥f(x)+α⋅[∇f(x)]Td
将该结果带入上式,有:
1 2 ! α 2 ⋅ d T [ ∇ 2 f ( x ) ] ⋅ d + O ( α 2 ⋅ ∣ ∣ d ∣ ∣ 2 ) ≥ 0 \frac{1}{2!} \alpha^2 \cdot d^T [\nabla^2 f(x)] \cdot d + \mathcal O(\alpha^2 \cdot ||d||^2) \geq 0 2!1α2⋅dT[∇2f(x)]⋅d+O(α2⋅∣∣d∣∣2)≥0 - 将不等式两侧同时除以
α
2
\alpha^2
α2,不等式符号不发生变化:
1 2 d T [ ∇ 2 f ( x ) ] ⋅ d + O ( α 2 ⋅ ∣ ∣ d ∣ ∣ 2 ) α 2 ≥ 0 \frac{1}{2} d^T [\nabla^2 f(x)] \cdot d + \frac{\mathcal O(\alpha^2 \cdot ||d||^2)}{\alpha^2} \geq 0 21dT[∇2f(x)]⋅d+α2O(α2⋅∣∣d∣∣2)≥0
在此基础上,令 α ⇒ 0 \alpha \Rightarrow 0 α⇒0,最终有:与凸函数一阶条件证明中的情况相似,其分子趋近0 0 0远远高于分母,因而有:lim α ⇒ 0 O ( α 2 ⋅ ∣ ∣ d ∣ ∣ 2 ) α 2 = 0 \begin{aligned}\mathop{\lim}\limits_{\alpha \Rightarrow 0} \frac{\mathcal O(\alpha^2 \cdot ||d||^2)}{\alpha^2} = 0\end{aligned} α⇒0limα2O(α2⋅∣∣d∣∣2)=0系数1 2 \begin{aligned}\frac{1}{2}\end{aligned} 21被忽略了~
d T [ ∇ 2 f ( x ) ] ⋅ d ≥ 0 d^T [\nabla^2 f(x)] \cdot d \geq 0 dT[∇2f(x)]⋅d≥0
这实际上就是半正定矩阵的定义。
从几何意义的角度观察,当
α
⇒
0
\alpha \Rightarrow 0
α⇒0时,方向
d
d
d任意取都不会影响
d
T
[
∇
2
f
(
x
)
]
⋅
d
≥
0
d^T [\nabla^2 f(x)] \cdot d \geq 0
dT[∇2f(x)]⋅d≥0,这说明
[
∇
2
f
(
x
)
]
[\nabla^2 f(x)]
[∇2f(x)]是半正定的。
强凸函数
强凸函数的定义
关于强凸函数的定义表示如下:设
f
(
⋅
)
f(\cdot)
f(⋅)为定义在空间
I
\mathcal I
I上的函数,若存在
m
>
0
m>0
m>0,使其对
I
\mathcal I
I上的任意两点
x
1
,
x
2
x_1,x_2
x1,x2与任意实数
λ
∈
(
0
,
1
)
\lambda \in (0,1)
λ∈(0,1)总有:
λ
⋅
f
(
x
1
)
+
(
1
−
λ
)
⋅
f
(
x
2
)
≥
f
[
θ
⋅
x
1
+
(
1
−
θ
)
⋅
x
2
]
+
m
2
⋅
θ
(
1
−
θ
)
⋅
∣
∣
x
1
−
x
2
∣
∣
2
\lambda\cdot f(x_1) + (1 - \lambda) \cdot f(x_2) \geq f[\theta \cdot x_1 + (1 - \theta) \cdot x_2] + \frac{m}{2} \cdot \theta(1 - \theta) \cdot ||x_1 -x _2||^2
λ⋅f(x1)+(1−λ)⋅f(x2)≥f[θ⋅x1+(1−θ)⋅x2]+2m⋅θ(1−θ)⋅∣∣x1−x2∣∣2
相比于凸函数的定义,强凸函数明显多了一个部分:
m
2
⋅
θ
(
1
−
θ
)
⋅
∣
∣
x
1
−
x
2
∣
∣
2
\begin{aligned}\frac{m}{2} \cdot \theta(1 - \theta) \cdot ||x_1 -x _2||^2\end{aligned}
2m⋅θ(1−θ)⋅∣∣x1−x2∣∣2。并且这个部分一定是正数。这相比凸函数仅仅
≥
0
\geq 0
≥0的约束要更强。
也被称作
m
m
m-强凸,其与凸函数定义的本质区别是相比凸函数多了一个
>
0
>0
>0下界的保证。
强凸函数的判定条件
和凸函数的判定条件相类似,关于强凸的判定条件同样没有直接对 f ( ⋅ ) f(\cdot) f(⋅)进行描述。对应条件表示如下:
- 定义
G
(
x
)
≜
f
(
x
)
−
1
2
m
⋅
∣
∣
x
∣
∣
2
\begin{aligned}\mathcal G(x) \triangleq f(x) - \frac{1}{2} m \cdot ||x||^2\end{aligned}
G(x)≜f(x)−21m⋅∣∣x∣∣2,有:
f ( ⋅ ) is m-Strong Convex ⇔ G ( x ) is Convex f(\cdot) \text{ is m-Strong Convex } \Leftrightarrow \mathcal G(x) \text{ is Convex} f(⋅) is m-Strong Convex ⇔G(x) is Convex
强凸函数的一阶条件
关于强凸函数的一阶条件是在对应凸函数一阶条件的基础上,加入一个二次下界:
和
f
(
⋅
)
f(\cdot)
f(⋅)梯度满足利普希兹连续对应的二次上界引理不同:
∇
f
(
⋅
)
Lipschitz
⇔
f
(
x
2
)
≤
f
(
x
1
)
+
[
∇
f
(
x
1
)
]
T
(
x
2
−
x
1
)
+
L
2
∣
∣
x
2
−
x
1
∣
∣
2
\nabla f(\cdot) \text{ Lipschitz} \Leftrightarrow f(x_2) \leq f(x_1) + [\nabla f(x_1)]^T (x_2 - x_1) + \frac{\mathcal L}{2}||x_2 - x_1||^2
∇f(⋅) Lipschitz⇔f(x2)≤f(x1)+[∇f(x1)]T(x2−x1)+2L∣∣x2−x1∣∣2
利普希兹连续强调的是限制梯度变化量的上界;而
m
m
m-强凸强调一个
>
0
>0
>0的二次下界。
f
(
⋅
)
is m-Strong Convex
⇔
f
(
x
2
)
≥
f
(
x
1
)
+
[
∇
f
(
x
1
)
]
T
(
x
2
−
x
1
)
+
m
2
∣
∣
x
2
−
x
1
∣
∣
2
f(\cdot) \text{ is m-Strong Convex } \Leftrightarrow f(x_2) \geq f(x_1) + [\nabla f(x_1)]^T (x_2-x_1) + \frac{m}{2}||x_2 - x_1||^2
f(⋅) is m-Strong Convex ⇔f(x2)≥f(x1)+[∇f(x1)]T(x2−x1)+2m∣∣x2−x1∣∣2
强凸函数的梯度单调性
和凸函数的梯度单调性基本类似,只不过下界由
0
0
0换成了:
证明过程略。
f
(
⋅
)
is m-Strong Convex
⇔
[
∇
f
(
x
)
−
∇
f
(
y
)
]
T
(
x
−
y
)
≥
m
⋅
∣
∣
x
−
y
∣
∣
2
f(\cdot) \text{ is m-Strong Convex } \Leftrightarrow [\nabla f(x) - \nabla f(y)]^T (x - y) \geq m \cdot ||x - y||^2
f(⋅) is m-Strong Convex ⇔[∇f(x)−∇f(y)]T(x−y)≥m⋅∣∣x−y∣∣2
强突函数的二阶条件
在
f
(
⋅
)
f(\cdot)
f(⋅)二阶可微的条件下,有:
其中
I
\mathcal I
I指单位矩阵。
f
(
⋅
)
is m-Strong Convex
⇔
∇
2
f
(
x
)
≽
m
⋅
I
f(\cdot) \text{ is m-Strong Convex } \Leftrightarrow \nabla^2 f(x) \succcurlyeq m \cdot \mathcal I
f(⋅) is m-Strong Convex ⇔∇2f(x)≽m⋅I
相关参考:
【优化算法】梯度下降法-基础补充-凸函数vs强凸函数vs严格凸函数(上)
【优化算法】梯度下降法-基础补充-凸函数vs强凸函数vs严格凸函数(下)
最优化理论与方法-第三讲-凸函数:定义与基本性质