4. 快速排序
>> 快速排序的思想
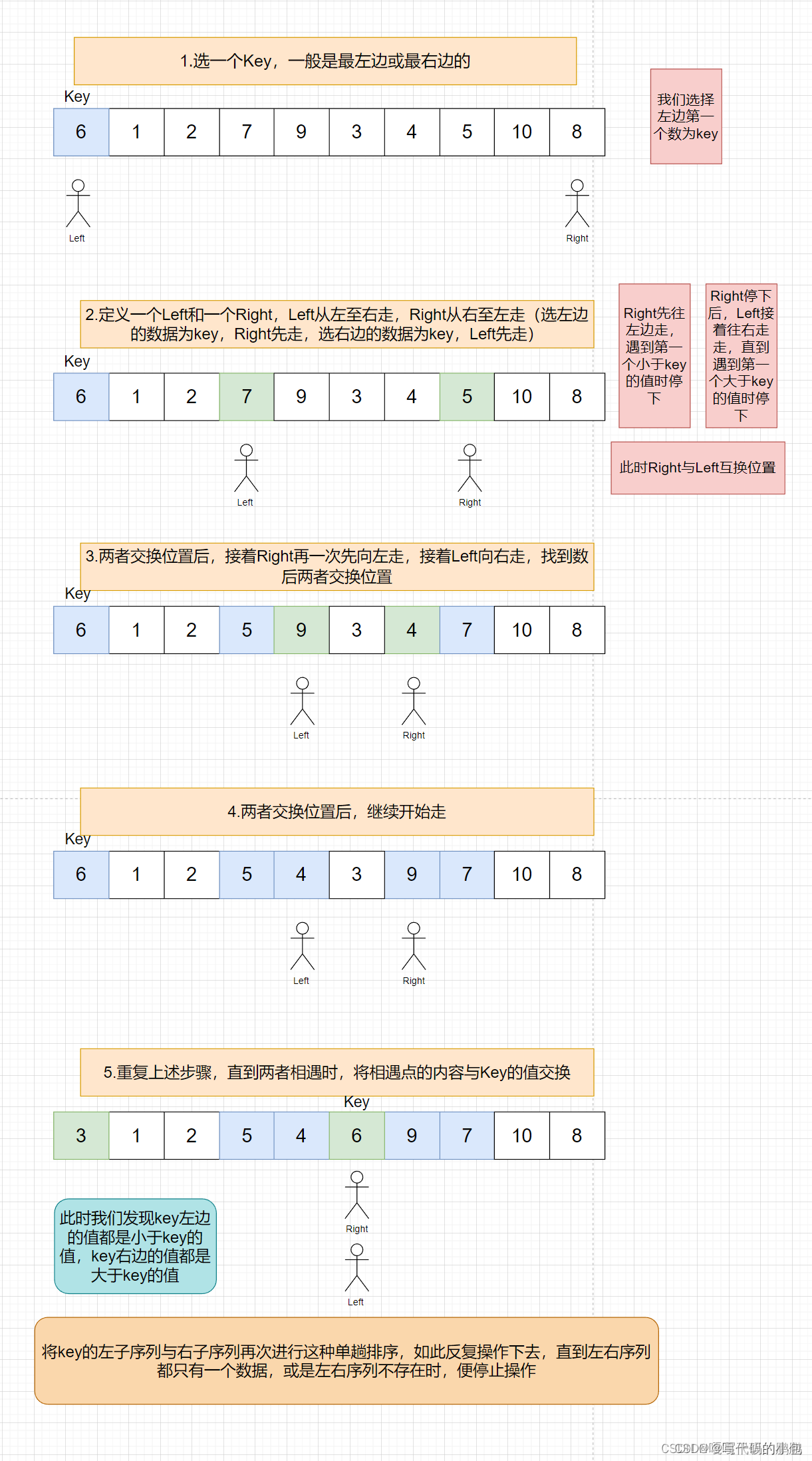
快速排序(QuickSort)是一种高效的排序算法,基于分治策略。它的原理可以概括为以下步骤:
-
选择一个基准元素(pivot),通常选择数组中的一个元素作为基准。这个基准元素将用来将数组分割为较小和较大的两个子数组。
-
分区过程(Partition):将数组中的元素重新排列,将所有比基准元素小的元素移动到其左边,所有比基准元素大的元素移动到其右边。基准元素的最终位置被确定,称为分区点(partition point),这个过程称为分区。
-
对两个子数组递归地应用上述过程。递归地将子数组分别进行分区,直到子数组的大小为零或一。递归的结束条件是当子数组的大小为零或一时,说明数组已经有序。
-
合并子数组:将所有子数组合并为最终的排序数组。
具体步骤如下:
- 选择基准元素,通常选择最右边的元素。
- 使用两个指针,一个指向数组的起始位置(low),另一个指向数组的结束位置(high)。
- 从起始位置开始,遍历数组,比较每个元素与基准元素的大小关系:
- 如果元素小于基准元素,将指针 i 向后移动一位,并交换指针 i 和 j 对应的元素。
- 如果元素大于或等于基准元素,只移动指针 j 向后移动一位。
- 当遍历结束时,将基准元素与指针 i 对应的元素交换位置,这样基准元素就处于正确的位置上。
- 以基准元素为界,将数组分为两个子数组。对左边的子数组和右边的子数组递归地应用上述过程,直到子数组的大小为零或一。
- 递归结束后,所有子数组都有序。将所有子数组合并起来,即得到最终的有序数组。
快速排序的平均时间复杂度为
O(n log n),其中 n 是待排序的元素数量。它是一种原地排序算法,不需要额外的空间。由于其高效性和普适性,快速排序是常用的排序算法之一。
>> 快速排序代码实现
package kfm.bases.Sort;
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 9, 1, 3, 2, 7, 3};
System.out.println("Original array: ");
printArray(arr);
quickSort(arr, 0, arr.length - 1);
System.out.println("\nSorted array: ");
printArray(arr);
}
public static void quickSort(int[] arr, int low, int high) {
// 检查左边界 low 是否小于右边界 high
if (low < high) {
// 调用 partition 方法来确定枢轴元素的正确位置,并返回此位置作为 pivotIndex
int pivotIndex = partition(arr, low, high);
// 对数组左边进行快排
quickSort(arr, low, pivotIndex - 1);
// 对数组右边进行快排
quickSort(arr, pivotIndex + 1,high);
}
}
// 确定枢轴元素的正确位置,并将数组分为两个子数组。
public static int partition(int[] arr, int low, int high) {
// 选取最右边元素轴元素
// int pivot = arr[high];
// int i = low - 1;
//
// for (int j = low; j < high; j++) {
// if (arr[j] > pivot) {
// i ++;
// swap(arr, i, j);
// }
// }
// swap(arr,i + 1, high);
// return i + 1;
// 选择最左边元素为轴元素
int left = low;
int right = high;
int base = arr[low];
while (left < right) {
while (left < right && arr[right] >= base) {
right--;
}
while (left < right && arr[left] <= base) {
left++;
}
swap(arr, left, right);
}
swap(arr, low, left);
return left;
}
// 输出数组元素
public static void printArray(int[] arr) {
for (int num : arr) {
System.out.print(num + " ");
}
System.out.println();
}
// 交换位置
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
在快速排序算法中,选择基准值的位置可以对算法的性能产生一定的影响。常见的选择基准值的方法有三种:选最左边元素、选最右边元素和选中间元素。
-
选最左边元素和选最右边元素作为基准值是最简单和最常见的两种方法,它们之间的主要区别在于分区操作的开始位置。如果选择最左边元素作为基准值,分区操作将从序列的左端开始,而选择最右边元素作为基准值,分区操作将从序列的右端开始。
-
在理想情况下,序列中的元素按照相对大小均匀分布,即序列近似有序。在这种情况下,选择最左边或最右边的元素作为基准值并不会导致分区不平衡的问题,因为分区操作的结果会大致均匀地将较小和较大的元素分布在两个子序列中。
-
然而,如果序列中的元素出现大量的重复元素,或者序列已经按照近似有序排列,那么选择最左边或最右边的元素作为基准值可能会导致分区不平衡的情况。这样会使得算法的时间复杂度退化到
O(n^2),而不是平均情况下的期望时间复杂度O(nlogn)。 -
为了避免这种情况,可以采用一些优化策略,如随机选择基准值、三数取中法(选取最左边、最右边和中间位置的元素的中位数作为基准值)等。这样可以增加算法的鲁棒性和适应性,降低时间复杂度的波动性。
综上所述,选择基准值的位置对快速排序算法可能会产生一定的影响,特别是在面对特定分布模式的输入数据时。因此,在实际应用中,根据具体情况选择合适的基准值选择策略,以获取更好的排序性能。