在计算傅里叶变换之前对信号去趋势是一种常见的做法,特别是在处理时间序列时。在这篇文章中,我将从数学和视觉上展示信号去趋势是如何影响傅里叶变换的。
这篇文章的目的是让介绍理解什么是常数和线性去趋势,为什么我们使用它们,以及它们是如何影响信号的傅里叶变换的。
傅里叶变换快速回顾
我们将使用傅里叶变换的如下定义:对于输入序列x[n],当n=0到n时,傅里叶变换的第k个系数为以下复数:
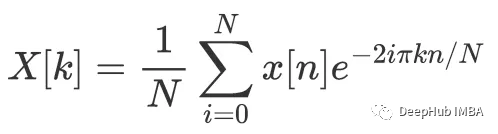
常量去趋势
序列x[n]可以分解如下:将其写成两个信号的和:“常数部分”等于信号的平均值,“平均值周围的可变性”部分给出实际信号与其平均值之间的差值:
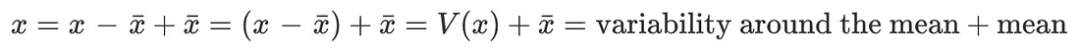
对于所有样本n,我们有:
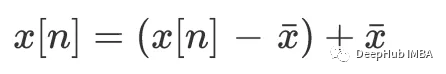
首先,求x均值的傅里叶变换
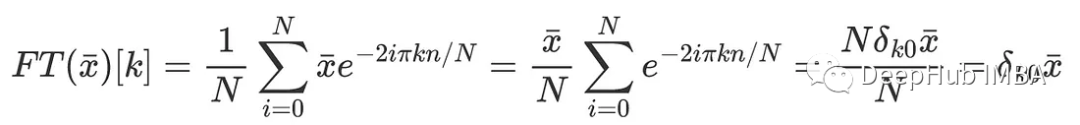
这是一个简单的序列,所以在k=0处x的均值为0,在其他地方的值也为0。
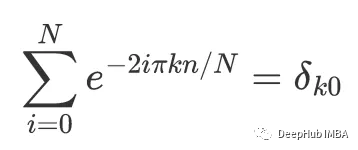
使用下面代码绘制所有指数也可以看到为什么它们的和总是为0(除了k=0)。
import numpy as np
import matplotlib.pyplot as plt
N = 10
ns = np.arange(N)
fig, axes = plt.subplots(1, N//2+1, figsize=(18,8), sharex=True, sharey=True)
for k in range(0, N//2+1):
eiks = np.exp(-2*1J*np.pi*ns/N*k)
pretty_ax(axes[k])
plot_sum_vector(eiks, axes[k])
axes[k].set_title(f'k={k}')
axes[k].set_aspect('equal')
fig.suptitle(f'Complex plot of the $e^{{-2i\pi kn/N}}$ families')

现在我们把x的傅里叶变换写成这样,分为两部分
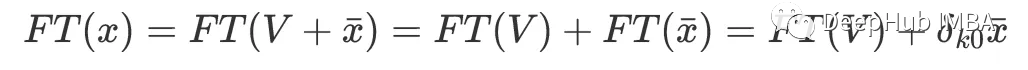
分解x的傅里叶变换,结果是2个傅里叶变换的和:“可变性”部分的傅里叶变换,以及k=0时等于平均值的系数。
也就是说x的傅里叶变换等于其可变性在均值附近的傅里叶变换的和,再加上除k = 0处之外的序列,这个序列都为0,所以他的均值是x。
这就常数去趋势,是在进行傅里叶变换之前去除信号的均值。对于傅里叶系数,就傅里叶系数而言,它对应于将k = 0系数设置为0。
k = 0的系数始终等于信号的平均值,可以使用下面方法证明:
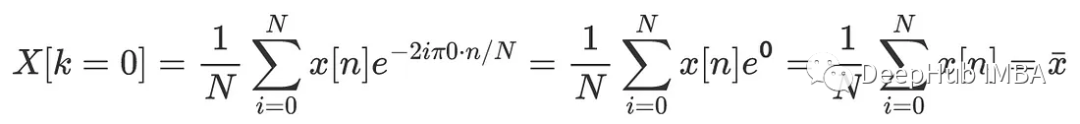
线性去趋势
方法与前面相同:将输入信号写为2个部分的和:“线性”部分,以及围绕该线性部分的其余变化:

这里的线性部分是从最小二乘拟合计算。利用指数,可以将线性部分写为:
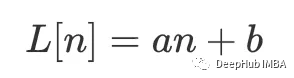
其中b是信号的平均值。让我们来看看它的傅里叶变换:
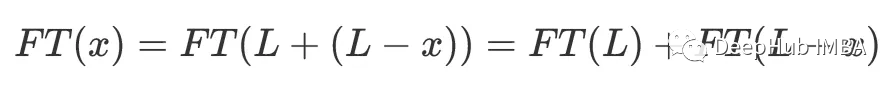
线性部分的傅里叶变换为,给定傅里叶变换的线性性质:
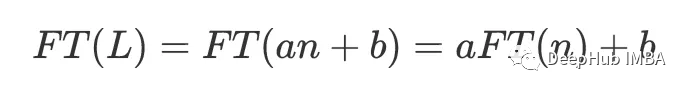
线性去趋势包括在进行傅里叶变换之前去除x的线性部分:它从结果中去除aFT(n)+b项,其中a是常数因子(对应于线性拟合的斜率),FT(n)是线性序列[0,1,…]的傅里叶变换,b是信号的平均值(因此第一个傅里叶系数将为0,就像常数去趋势一样)。
python代码
在Python中使用numpy和scipy实现非常简单。
Scipy在它的signal 包中提供了detrend函数,带有一个类型参数来指定我们是想让信号保持常量趋势还是线性趋势。
在下面的例子中,创建了一个长度为20个样本的信号,其中包含一个前导系数为2的线性部分,一个噪声,一个偏移量为4的正弦部分。
import numpy as np
from scipy.signal import detrend
import matplotlib.pyplot as plt
N = 20
# create a sample signal, with linear, offset, noise and sinus parts
ys = np.arange(N) * 2 + 4 + np.random.randn(N) + 4*np.sin(2*np.pi*np.arange(N)/5)
# constant and linear detrend
ys_c = detrend(ys, type='constant')
ys_l = detrend(ys, type='linear')
fig, axes = plt.subplots(1, 2)
ax = axes[0]
ax.plot(ys, label='raw')
ax.plot(ys_c, label='constant-detrended')
ax.plot(ys_l, label='linear-detrended')
ax.legend()
ax.set_title('Input signal')
ax = axes[1]
# we use rfft since our input signals are real
ax.plot(np.abs(np.fft.rfft(ys)))
ax.plot(np.abs(np.fft.rfft(ys_c)))
ax.plot(np.abs(np.fft.rfft(ys_l)))
ax.set_title('Module of Fourier-transform')
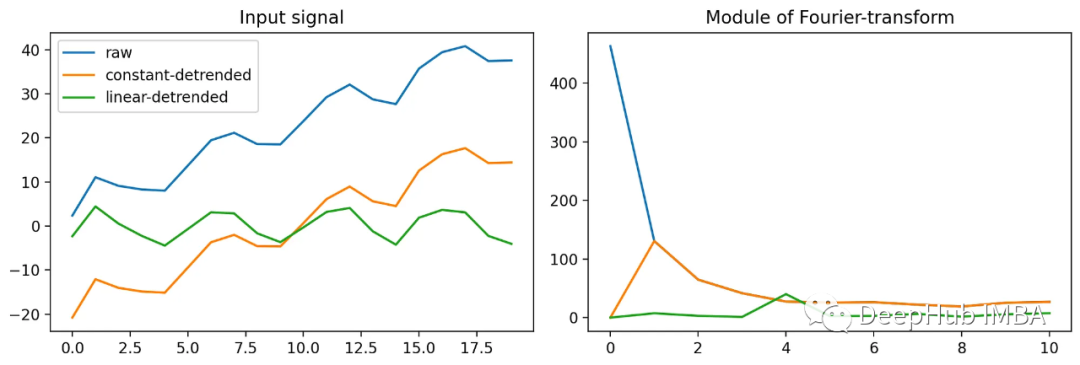
在左边我们有原始输入信号,以及它的常数去趋势和线性去趋势版本。
常数去趋势有效地去除信号的平均值,使其在0附近居中。线性去趋势不仅去掉了信号的平均值,而且还去掉了它的线性趋势(又名“直线斜率”)。从视觉上看,在线性去趋势信号上比在原始信号上更容易发现正弦部分。
右边是每个信号的傅里叶变换模块:如果不去除趋势,我们得到蓝色模块。使用常数去趋势法去除平均值可以有效地将0系数设置为0,这在大多数情况下使得图表更容易分析。自线性去趋势的结果是最好的:输出傅里叶系数很好地显示了输出频谱中的频率,线性去趋势的主要优点是它大大减少了频谱泄漏。
线性信号的傅里叶变换
对于不同的K值,我们可以很容易地画出线性信号Kn (K为斜率)的傅里叶变换:
import numpy as np
import matplotlib.pyplot as plt
N = 10
ns = np.arange(N)
Ks = [-5, 2, 5]
fig, axes = plt.subplots(len(Ks), N//2+1, figsize=(18,8), sharex=True, sharey=True, gridspec_kw={'hspace':0, 'wspace':0})
for i, K in enumerate(Ks):
xs = K*np.arange(N)
for k in range(0, N//2+1):
Zs = xs * np.exp(-2*1J*np.pi*ns/N*k) / N
ax = axes[i, k]
pretty_ax(ax)
plot_sum_vector(Zs, ax)
ax.set_aspect('equal')
ax.set_xlabel(f'k={k}')
axes[i, 0].set_ylabel(f'K={K}')
fig.tight_layout()
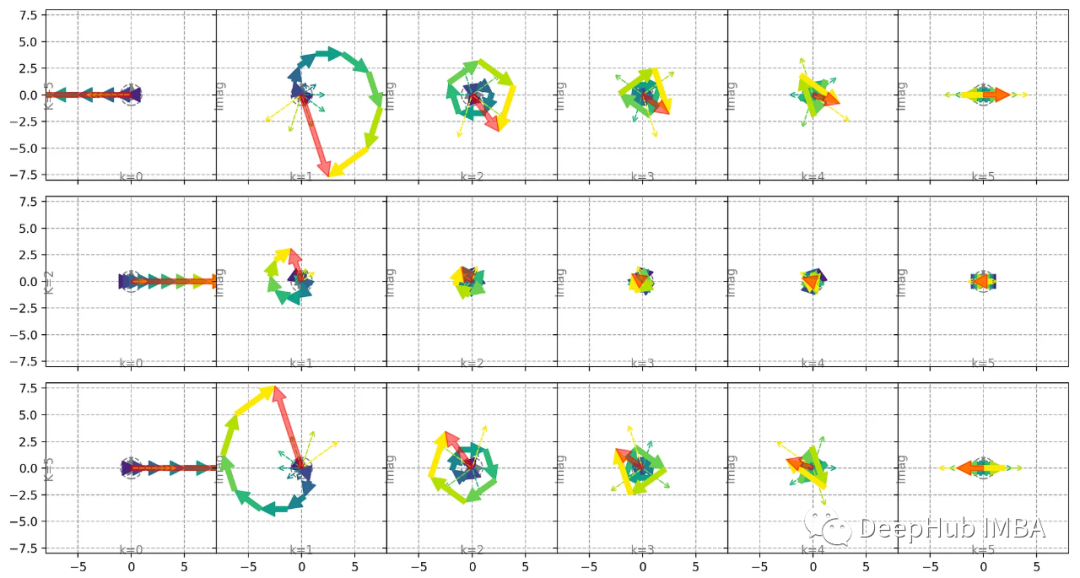
对于给定的k值,用红色箭头表示的傅里叶系数总是对齐的,并且等于一个比例。所以输出频谱中被去掉的部分总是序列[0,1,…N]的傅里叶变换的部分,其比例因子由线性拟合的斜率给出。
总结
在这篇文章中,我们介绍了常量和线性去趋势:它们分别由去除输入信号的平均值或线性拟合组成。在计算傅里叶变换之前的预处理步骤有助于使输出谱更容易解释。
去除信号的平均值使第0个系数为0。结果图更容易检查,因为大多数情况下,平均值与频谱的其余部分相比可能相当大。如果我们去掉这个系数,y轴的尺度就更容易设定。
线性去趋势除了去掉平均值也去掉了信号中的总体趋势,这通常是原始信号的主导部分,这样可以去掉其他成分例如季节行为等,所以如果需要对季节性进行分析还需要另外的处理。
https://avoid.overfit.cn/post/84dd016b15e440c3a9bf8c7c08a4adb4
作者:Yoann Mocquin






![心法利器[96] | 写了个向量检索的baseline](https://img-blog.csdnimg.cn/img_convert/eb10d569baae3f985f0ae7303e3be17d.png)