在上一篇中，我们介绍了ECEF坐标系和经纬度的互换。

本篇，主要介绍已知A\B两个点的经纬度，如何求取椭球上的最短距离、路径。

在标准椭球面上，从A点运动到B点，距离如何，轨迹、每个阶段的方向又是如何呢？ 要讨论方向，会引出两个概念。第一个是切平面坐标系，这是讨论"方向"的基础。第二个是运动，即考虑不同时刻、不同位置之间的关系与变化规律。

1 切面坐标系

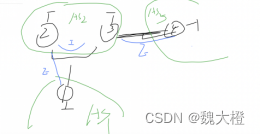
站在地表，一般使用的是东北坐标系ENU，即切平面坐标。从ECEF坐标转换为ENU （East-North-Up）坐标，如下如所示：

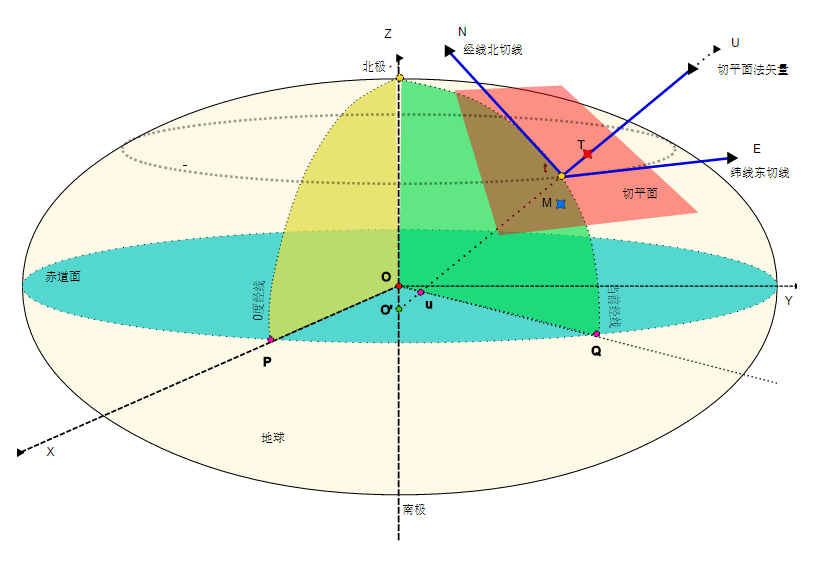
图中，由法向量$\overrightarrow{tT}$定义的切平面构成了“天圆地方”的参考平面。法向量就是这个坐标系的Z轴。由于尺度不变，这个坐标系和ECEF坐标系是一个旋转关系。

E(East) 单位矢量在经度、纬度均为0度时，切面坐标系的E轴恰好指向正东，就是ECEF的Y方向，取值{0,1,0} 。当经度提高，在X-方向开始有了投影。坐标轴E和纬度无关。旋转经度$\theta$后得到；ECEF坐标系下，E轴的单位矢量：

E ⃗ = { − sin ⁡ θ , cos ⁡ θ , 0 } \vec E=\{-\sin \theta,\cos \theta,0\} E ={−sinθ,cosθ,0}

N(North) 单位矢量在经度、纬度均为0度时，切面坐标系的E轴恰好指向正北，就是ECEF的Z方向，取值{0,0,1} 。当纬度上升时，在X-方向开始有了投影；ECEF坐标系下，N轴的单位矢量：

N ⃗ = { − sin ⁡ φ c o s θ , − sin ⁡ φ sin ⁡ θ , cos ⁡ φ } \vec N=\{-\sin \varphi cos\theta,-\sin \varphi \sin \theta,\cos \varphi\} N ={−sinφcosθ,−sinφsinθ,cosφ}

U(Up) 单位矢量在经度、纬度均为0度时，切面坐标系的E轴恰好指向{1,0,0}方向。经过纬度旋转、经度旋转后，ECEF坐标系下，U轴的单位矢量：

U ⃗ = { cos ⁡ φ c o s θ , cos ⁡ φ sin ⁡ θ , sin ⁡ φ } \vec U=\{\cos \varphi cos\theta,\cos \varphi \sin \theta,\sin \varphi\} U ={cosφcosθ,cosφsinθ,sinφ}

要计算站在t位置下，查看任意一点 M 的 ENU 坐标，只要执行运算

$$\begin{gathered} {\overrightarrow{M_{ENU}}}^T=\left[\begin{array}{c}\vec{E} \\ \vec{N} \\ \vec{U}\end{array}\right]\times {\left(\overrightarrow{M_{ECEF}}-\vec{t}\right)}^T=R\times {\left(\overrightarrow{M_{ECEF}}-\vec{t}\right)}^T \end{gathered}$$

上式中坐标都是行向量,转置后是列向量。需要注意的是，这个旋转矩阵R的左逆、右逆都是自身的转置,故而两类坐标的转换就很方便了。

$$R=\left[\begin{array}{ccc}-\sin \theta & \cos \theta & 0\\ -\sin \phi cos\theta & -\sin \phi \sin \theta & \cos \phi \\ \cos \phi cos\theta & \cos \phi \sin \theta & \sin \phi \end{array}\right]$$

$$R\times R^T=R^T\times R=I$$

2 计算椭球轨迹

椭球的最短路径是一个三维空间曲线。在轨迹的各个位置上，由于经纬度不同，椭球的曲率不断变化。同时，理想参考椭球是局部平坦的凸曲面，没有陡峭的局部峰和谷，这使得可以通过"碎步迭代"的方法，较为精确地获得最短路径。

迭代命题：已知起点A、终点B的经纬度，求取在高度H上从A运动到B的最短椭球路径，并计算总距离。

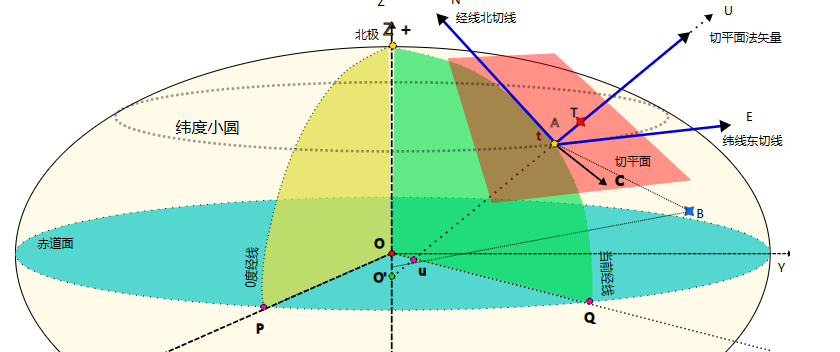
设置距离数值积分量$D$ 初始化为0.

迭代步骤:

(1) 在当前ENU坐标系下确定方向

把 A,B换算到ECEF下，此刻ECEF向量$\overrightarrow{B-A}$在切平面上的投影指示了最佳方向。在A点建立ENU坐标系，A是原点，此时，B的ENU坐标：

$$\begin{gathered} {\vec{B}}_{ENU}=\left[\begin{array}{c}{E}_B \\ {N}_B \\ {U}_B\end{array}\right]=R_A\times {\left(\vec{B}-\vec{A}\right)}^T \end{gathered}$$

在ENU坐标系里，方向定义为正北为0度，顺时针递增:

$$\tan C=\frac{E_B}{N_B}$$

计算出C后，即可计算ENU单位矢量

C E N U ⃗ = { sin ⁡ C , cos ⁡ C , 0 } \vec{C_{ENU}}=\{ \sin C, \cos C,0 \} CENU​ ​={sinC,cosC,0}

该单位矢量转换到 ECEF下为

$$\overrightarrow{C^T}=R_A^T\overrightarrow{C_{ENU}}$$

(2) 小步推进

已经知道当前起点A、初始方向C后，在以当前位置A为原点的ENU坐标系下，沿着设置的方向前进一个小距离$\Delta$, 得到下一个位置 A’。

由于$\Delta$很小，我们认为当前行进的距离，就是以A所在位置为切面的正球上行进的距离。

A 的正球坐标为 A s ⃗ = A ⃗ + { 0 , 0 , − d } \vec {A_s}= \vec A +\{0,0,-d\} As​ ​=A +{0,0,−d}

同时，方向C的单位矢量不受平移的影响，指向不变，$\overrightarrow{C_s}=\vec{C}$。

沿着方向矢量${\vec{C}}_s$、正球矢量$\overrightarrow{A_s}$生成的正圆，从矢量$\overrightarrow{A_s}$处，旋转$\omega$弧度，就是下一个位置的正球坐标。旋转的弧度可以用下式求解。

$$cos\omega =\frac{\Delta }{r_A+H}$$

这里关键是通过弧度得到旋转后的矢量A’,需要用到三维旋转，也就是罗德里格旋转公式.

设

$$\vec{\mu }=\frac{{\vec{A}}_s\otimes \overrightarrow{C_s}}{\left|{\vec{A}}_s\right|}$$

$$\overrightarrow{A_s^{\prime }}=cos\omega \cdot \overrightarrow{A_s}+(1-\cos \omega )(\vec{\mu }\odot \overrightarrow{A_s})+sin\omega \cdot \vec{\mu }\otimes \overrightarrow{A_s}$$

由于法向量本身就是垂直的，因此投影项为0，上式简化为:
$$\overrightarrow{A_s^{\prime }}=cos\omega \cdot \overrightarrow{A_s}+sin\omega \cdot \vec{\mu }\otimes \overrightarrow{A_s}$$

最后，把正球下的坐标系平移到ECEF

A ’ ⃗ = A s ′ ⃗ + { 0 , 0 , d } \vec {A’}= \vec {A'_s} +\{0,0,d\} A’ =As′​ ​+{0,0,d}

通过A’的ECEF，计算A’的经纬度坐标，并设置高度为H。此时，A’的经纬度就是下一位置。

(3) 距离累加

由于$\Delta$很小，我们认为当前行进的距离，就是以A所在位置为切面的正球上行进的距离。

$$D=D+(r_A+H)\omega$$

(4) 继续迭代

推进A到新的位置 A’

$$A=A^{\prime }$$

并转到(1)。

(5)收敛条件

当A、B距离小于$\Delta$时，以AB的正球距离为距离，最终确定总距离。

3 进行测试

设置起点与终点，进行测试：

void demo_ellips_geodesic()
{
	printf("\n\n");
	const double LLA_A[] = {31.847774515, 117.292115092, 10000};
	const double LLA_B[] = {37.807300349, -122.366731167,10000};

	const int maxRes = 32768;
	double (* lla)[3] = new double [maxRes][3];
	double (* ecef)[3] = new double [maxRes][3];
	double * distance = new double [maxRes];
	double * direction = new double [maxRes];
	double * err = new double [maxRes];
	using namespace CES_GEOCALC;

	const int step = 1000;

	int res = ellips_geodesic(LLA_A,LLA_B,maxRes,100000/step,lla,ecef,distance,direction,err,false,true,step);

	for(int i=0;i<res;++i)
	{
		printf("I=%d LAT=%12.7lf LON=%12.7lf ALT=%7.1lf DIS=%8.1lf DIR=%12.7lf ERR=%lf\n",
			   i,
			   lla[i][0],lla[i][1],lla[i][2],
			   distance[i],direction[i],err[i]
			   );
	}

	delete [] lla;
	delete [] ecef;
	delete [] distance;
	delete [] direction;
	delete [] err;
}

输出：

I=0 LAT=  31.8477745 LON= 117.2921151 ALT=10000.0 DIS=  1000.0 DIR=  43.0147959 ERR=9113951.151266
I=1 LAT=  32.5040600 LON= 118.0168980 ALT=10000.0 DIS=101000.0 DIR=  43.3985947 ERR=9043525.166938
I=2 LAT=  33.1560649 LON= 118.7522233 ALT=10000.0 DIS=201000.0 DIR=  43.7951513 ERR=8972543.435380
I=3 LAT=  33.8036190 LON= 119.4984456 ALT=10000.0 DIS=301000.1 DIR=  44.2047633 ERR=8901010.433060
I=4 LAT=  34.4465456 LON= 120.2559264 ALT=10000.0 DIS=401000.1 DIR=  44.6277359 ERR=8828930.668846
……
I=102 LAT=  37.8073003 LON=-122.3667312 ALT=10000.0 DIS=10143664.8 DIR= 132.8475527 ERR=0.000000

此轨迹在莫卡托投影下会发生形变，如下图：

4 完整工程

代码与工程参考

https://gitcode.net/coloreaglestdio/geocalc/-/blob/master/geocalc.h