文章目录
- 《线性调频雷达典型有源干扰抑制技术研究》 阅读记录
- (1)研究背景与意义:
- (2)有源压制干扰
- (3)有源欺骗式干扰
- (4)压制干扰的抑制
- (5)欺骗干扰的抑制
- (6)新型干扰的抑制
- (7)基于自适应频域对消的噪声调幅抑制
- 1、基于频域对消的干扰抑制方法
- 2.噪声调幅干扰参数估计模型
- 3.基于ML的参数估计方法
- 4.基于修正傅里叶插值的粗估计
- (8)基于多步干扰消除的完全转发式干扰抑制技术
- (9)基于EEMD的部分转发干扰抑制技术
- (10)基于时-频域联合处理的卷积式灵巧噪声干扰抑制
- SMSP和C&I干扰介绍
- SMSP介绍
- (一)干扰过程介绍
- (二)特性机理
- C&I介绍
- (一)干扰过程介绍
- (二)C&I干扰机理介绍
- SMSP和C&I干扰识别
- SMSP干扰识别
- (一)基于相位的差分识别
- (二)基于干扰调频斜率的SMSP识别
《线性调频雷达典型有源干扰抑制技术研究》 阅读记录
(1)研究背景与意义:
针对目前广泛使用的LFM体制雷达,如脉冲压缩(PC)和脉冲多普勒(PD)雷达,干扰机普遍使用数字射频存储器(DRFM)和直接数字式频率合成器(DDS)。主要是对所截获雷达发射信号的波形进行高精度复制,使产生的干扰信号在经过匹配滤波器后,功率几乎没有任何损失。同时,干扰机利用DDS技术,可以对干扰进行移频处理。而LFM信号的时延与移频是强耦合的,因此DDS移频可以产生超前的假目标干扰。
以上技术大幅度妨碍了雷达对真实目标的检测,需要研究相应的干扰对抗措施来保证其的正常工作。
(2)有源压制干扰
其原理是利用功率较高的类噪声干扰掩盖目标信号,阻碍雷达探测到真实目标,这类干扰主要针对早期的微波雷达和单脉冲雷达所提出的,具有非常好的干扰能力,但是在面对LFM波形时,由于其在接收端通过匹配滤波,充分利用了PC的性能增益,极大的提高了目标回波在进行CFAR时所需要的信噪比。对于功率受限的干扰机,通常无法满足遮盖目标所需要的最少发射功率。目前仍在使用的典型有源压制干扰主要有噪声调幅和噪声调相干扰等。
(3)有源欺骗式干扰
其原理是产生和真实目标回波相干的干扰信号,从而使雷达无法完全分辨出干扰和真实目标。几乎所有的有源欺骗式干扰都是基于DRFM技术的干扰机产生(如:截断交错干扰,间歇采样转发干扰,间歇采样重复转发干扰以及间歇采样移频转发干扰)。此外还有污迹频谱干扰,卷积式灵巧噪声干扰等不仅可以产生超前真实目标的回波,还具有一定的压制效果。
(4)压制干扰的抑制
在早期,主要通过时域,变换域进行滤波处理的方式,实现压制干扰的抑制,但是随着LFM体制雷达的出现,在现有发射功率的条件下,很难对LFM体制的雷达实现压制干扰。但是有一些压制干扰抑制技术的研究如下:
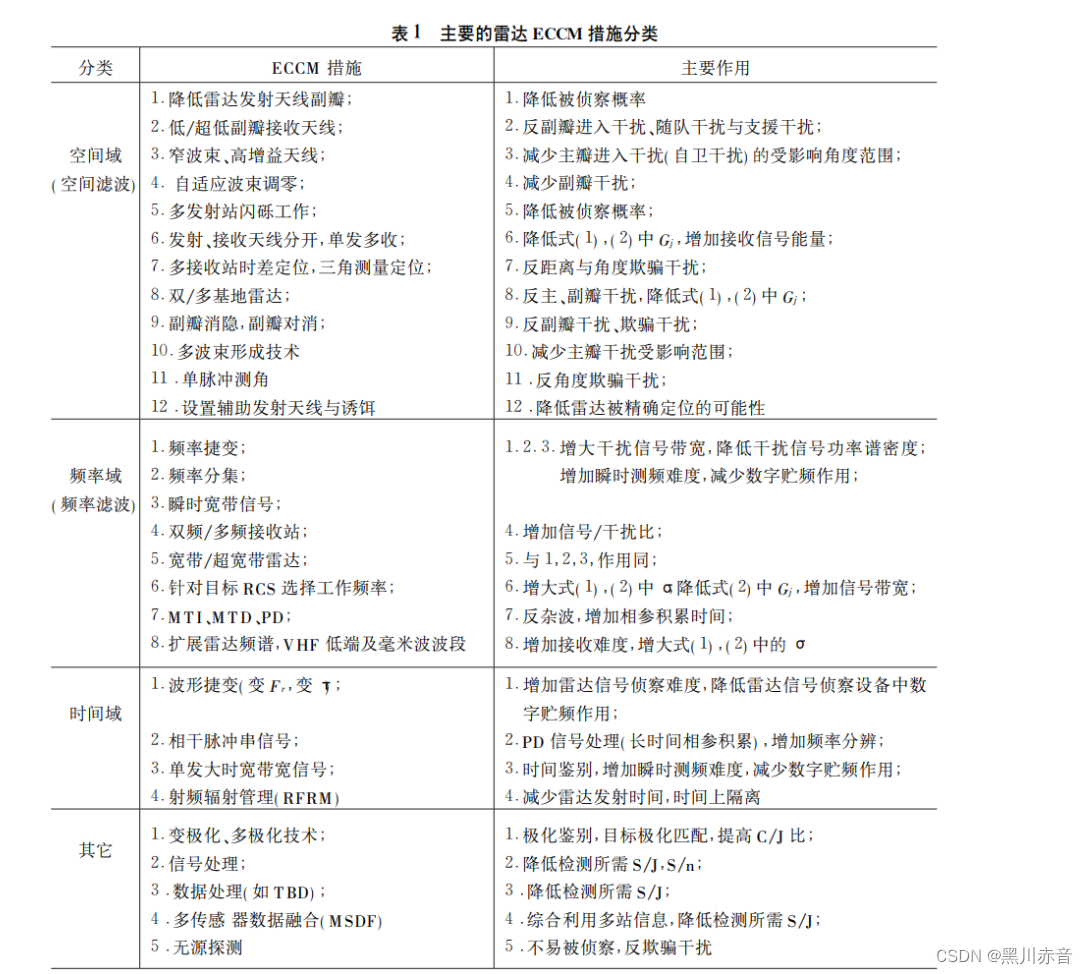
又有塔形的自适应匹配滤波追踪方法(主要是利用信号的各个组成部分相关性较好,而噪声的各个组成部分相关性较差,在不知道噪声的统计特征的情况下)对噪声进行有效的抑制。又有将稀疏分解的方法应用到压制干扰的抑制中,通过对信号的重构,获得目标回波的特征成分,来完成对噪声干扰的抑制;也可以使用Hough变换,检测到强杂波干扰下的微小目标,具有抑制效果;也可以使用基于高阶累积量的盲源分离方法对接收信号进行处理,在一定程度上可以抑制压制性干扰。
针对特定压制式干扰样式,如噪声调幅干扰,但是由于其干扰能量强于信号能量的特点使得干扰信号的参数可以被估计出来,然后利用频域对消,可以很好的抑制噪声调幅干扰。又有在估计出信号参数之后,对接收信号进行数学变换,将其分解为相位不变的信号和相位变换的杂波,之后进行相位变换得到有效的信号之后,进行二元检测;对于噪声调频干扰,由于其噪声的大带宽导致干扰的大带宽和雷达接收的中放带宽较小,在电路暂态响应的作用下,使得雷达接收的信号的包络跌宕起伏,导致其频率随机,相位随机,幅度也随机给目标检测带来较大的障碍,然而,有文献提出了使用小波变换,利用目标信号和噪声信号不相关的特征将有用信号和杂波信号分离出来进而克制噪声调频干扰。
(5)欺骗干扰的抑制
随着高速集成电路技术和数字信号处理技术的发展,各种使用DRFM和DDS技术的欺骗式干扰样式层出不穷,产生的假目标信号不仅具有更强的迷惑性而且数目众多,使得LFM雷达跟踪器饱和而且无法正常工作。
欺骗干扰主要分为两类,一类是托引式欺骗干扰(干扰机截获到雷达的照射脉冲后,以尽可能小的延时转发一个干扰脉冲,其幅度 U j U_j Uj 大于回波幅度 U s U_s Us,使得雷达自动增益控制电路受到影响,从而被干扰脉冲所控制,然后逐渐增加转发脉冲的延迟时间使得波门逐渐脱离真实目标,然后关机,使得雷达丢失跟踪目标,只好重新搜索)这种方法可以用小波分析克制(开始干扰实际上是在雷达测距函数上叠加了一个速度,叠加的这个速度会引起测距函数的突变,一般情况下速度较大,就可以用小波的奇异检测来检测出是什么时候施加的干扰)。
另一种干扰是转发式干扰,对转发式干扰进行去斜,并通过一定的处理使真实目标与转发式干扰的频率具有显著区别,然后设计合适的滤波器实现干扰抑制。对于移频式转发干扰(即 exp ( − j 2 π ( f c t + K π t 2 ) \exp(-j2\pi(f_ct+K\pi t^2) exp(−j2π(fct+Kπt2)到 exp ( − j 2 \exp(-j2 exp(−j2 π ( f c t + f d t + K π t 2 ) \pi(f_ct + f_dt + K\pi t^2) π(fct+fdt+Kπt2) ,附加的频移 f d f_d fd使信号的包络产生时移导致假目标的产生),这种干扰会有两种情况,一种是强回波干扰信号抑制弱回波干扰信号,使雷达完全看不到真目标回波;另一种可能是会同时出现一个较强的干扰信号和一个较弱的回波信号,但雷达的跟踪波门会被较强的干扰信号所捕获,导致雷达给出错误的距离信息。但是这个错误的距离信息也隐藏了真实的目标回波的距离信息,但是距离信息之差可以表示为 Δ S = c f d / 2 K \Delta S = cf_d/2K ΔS=cfd/2K ,利用干扰的假目标的距离信息解算出 f d f_d fd ,根据此处理进行距离补偿就可以实现对真目标的追踪。
(6)新型干扰的抑制
对于SMSP干扰(脉冲压缩雷达发射线性调频信号,其载频在脉冲内宽度是随时间按线性按线 性规律 变化的 , DRFM接收并储存该信号并在时域上对其采样,假设采样点数为N,那么采样后将时钟频率提高为 n n n倍,对采样数据进行抽取并按原顺序进行排序,然后对排序后的信号复制 n n n次,得到信号的干扰样式,即为SMSP干扰。由以上干扰可知,其导致了干扰信号与雷达信号含有不同的调频斜率,经过多次重复使得SMSP含有多个结构相同的子脉冲。由于其与雷达的相似结构,使得其可以在雷达输出端产生多瓣。当干扰概率较大时,其具有欺骗和压制的双重作用。)有团队提出匹配变换的方法进行识别(根据调频斜率的不同将信号分离出来)然后构造出抗干扰滤波器来进行克制。
对于C&I干扰(C&I干扰的产生过程为:(1)Chopping阶段,截取雷达信号不同的段,这些小段都是雷达信号的一部分,且含有不同的时间段和频率分布。(2)Interleaving阶段,将小段信号复制到相邻的间隙中,此时就产生了C&I干扰。其和匹配滤波器是相匹配的,因此可以在雷达接收端产生虚假目标,达到欺骗的效果。)可以使用模糊函数检测来进行抑制。
(7)基于自适应频域对消的噪声调幅抑制
1、基于频域对消的干扰抑制方法
假设能够精确的获取干扰的载频偏差和初始相位信息,那么就可以将接收信号中的噪声调幅干扰转变为一个实信号。干扰经过DFT后,干扰信号的正频部分和负频部分相互共轭,而真实目标回波信号不具备这样的性质,从而能够在频域中消除干扰。虽然在频域相互对消的过程中,会引入新的干扰信号,但是该干扰信号无法通过PC获得性能增益。如下:
r
(
t
)
=
s
(
t
)
+
[
A
+
ξ
1
(
t
)
]
⋅
e
j
(
w
t
+
θ
)
+
ξ
0
(
t
)
r\bigl(t\bigr)=s\bigl(t\bigr)+\bigr[A+\xi_1\bigl(t\bigr)\bigr]\cdot e^{j\bigl(w t+\theta\bigr)}+\xi_0\bigl(t\bigr)
r(t)=s(t)+[A+ξ1(t)]⋅ej(wt+θ)+ξ0(t)
做如下数学变换:
r
1
(
t
)
=
r
(
t
)
⋅
e
−
j
(
2
m
w
t
+
θ
)
=
A
+
ξ
1
(
t
)
+
s
(
t
)
⋅
e
−
j
(
w
t
+
θ
)
+
ξ
0
(
t
)
⋅
e
−
j
(
w
t
+
θ
)
r_1\big(t\big)=r\big(t\big)\cdot e^{-j\left(2mwt+\theta\right)}=A+\xi_1\big(t\big)+s\big(t\big)\cdot e^{-j\left(wt+\theta\right)}+\xi_0\left(t\right)\cdot e^{-j\left(wt+\theta\right)}
r1(t)=r(t)⋅e−j(2mwt+θ)=A+ξ1(t)+s(t)⋅e−j(wt+θ)+ξ0(t)⋅e−j(wt+θ)
基于这样一个事实:实信号的傅里叶变化的正频率和负频率部分是共轭对称的,然而信号和噪声部分不会有这样的特征,在做如下数学变换:
R
2
(
f
)
=
R
1
(
f
)
−
R
1
∗
(
−
f
)
R_2(f)=R_1(f)-R_1^*(-f)
R2(f)=R1(f)−R1∗(−f)
则:
r
2
(
t
)
⋅
e
j
(
w
t
+
θ
)
=
s
(
t
)
+
ξ
0
(
t
)
+
[
s
∗
(
t
)
+
ξ
0
∗
(
t
)
]
⋅
e
j
2
(
w
t
+
θ
)
r_2\left(t\right)\cdot e^{j\left(w t+\theta\right)}=s\left(t\right)+\xi_0\left(t\right)+\left[s^*\left(t\right)+\xi_0^*\left(t\right)\right]\cdot e^{j2\left(w t+\theta\right)}
r2(t)⋅ej(wt+θ)=s(t)+ξ0(t)+[s∗(t)+ξ0∗(t)]⋅ej2(wt+θ)
2.噪声调幅干扰参数估计模型
设噪声调幅信号的离散观测模型,假设接收机的采样率为
f
s
f_s
fs,共采样N个点,则待估计的噪声调幅信号的数学模型为:
z
n
=
[
A
+
ξ
1
(
n
)
]
⋅
e
j
(
w
n
/
f
,
+
θ
)
+
ξ
0
(
n
)
,
n
=
1
,
…
,
N
z_n=\left[A+\xi_1(n)\right]\cdotp e^{j(wn/f,+\theta)}+\xi_0(n),n=1,\ldots,N
zn=[A+ξ1(n)]⋅ej(wn/f,+θ)+ξ0(n),n=1,…,N
令
ϕ
n
=
w
m
/
f
S
+
θ
\phi_n = wm/f_S + \theta
ϕn=wm/fS+θ ,则也可表示为:
z
n
=
A
e
j
ϕ
n
+
ξ
1
(
n
)
e
j
ϕ
n
+
ξ
0
(
n
)
,
n
=
1
,
…
,
N
z_n=Ae^{j\phi_n}+\xi_1(n)e^{j\phi_n}+\xi_0(n),n=1,\ldots,N
zn=Aejϕn+ξ1(n)ejϕn+ξ0(n),n=1,…,N
3.基于ML的参数估计方法
假设非圆对称复高斯加性噪声为
ξ
(
n
)
\xi(n)
ξ(n) ,其实部与虚部的形式如下:
Re
{
ξ
(
n
)
}
=
ξ
1
(
n
)
cos
ϕ
n
+
Re
{
ξ
0
(
n
)
}
Im
{
ξ
(
n
)
}
=
ξ
1
(
n
)
sin
ϕ
n
+
Im
{
ξ
0
(
n
)
}
\begin{aligned}\operatorname{Re}\left\{\xi(n)\right\}=\xi_1(n)\cos\phi_n+\operatorname{Re}\left\{\xi_0(n)\right\}\\\\\operatorname{Im}\left\{\xi(n)\right\}=\xi_1(n)\sin\phi_n+\operatorname{Im}\left\{\xi_0(n)\right\}\end{aligned}
Re{ξ(n)}=ξ1(n)cosϕn+Re{ξ0(n)}Im{ξ(n)}=ξ1(n)sinϕn+Im{ξ0(n)}
计算实部和虚部的方差 $ \sigma_{sn}^2$和
σ
c
n
2
\sigma_{cn}^2
σcn2 ,则在第
n
n
n个点,加性噪声实部和虚部的联合概率密度为:
p
n
=
1
2
π
σ
c
n
σ
c
n
1
−
ρ
n
2
exp
{
−
R
e
2
{
ξ
(
n
)
}
σ
c
n
2
−
2
ρ
n
σ
c
n
σ
m
R
e
{
ξ
(
n
)
}
I
m
{
ξ
(
n
)
}
σ
c
n
σ
m
+
I
m
2
{
ξ
(
n
)
}
σ
m
2
2
(
1
−
ρ
n
2
)
}
p_n=\frac1{2\pi\sigma_{cn}\sigma_{cn}\sqrt{1-\rho_n^2}}\exp\left\{-\frac{\frac{\mathrm{Re}^2\left\{\xi(n)\right\}}{\sigma_{cn}^2}-\frac{2\rho_n}{\sigma_{cn}\sigma_m}\frac{\mathrm{Re}\left\{\xi(n)\right\}\mathrm{Im}\left\{\xi(n)\right\}}{\sigma_{cn}\sigma_m}+\frac{\mathrm{Im}^2\left\{\xi(n)\right\}}{\sigma_m^2}}{2\left(1-\rho_n^2\right)}\right\}
pn=2πσcnσcn1−ρn21exp⎩
⎨
⎧−2(1−ρn2)σcn2Re2{ξ(n)}−σcnσm2ρnσcnσmRe{ξ(n)}Im{ξ(n)}+σm2Im2{ξ(n)}⎭
⎬
⎫
假设噪声调幅干扰信号的离散观测值可以写为
z
n
=
x
n
+
j
y
n
z_n = x_n + jy_n
zn=xn+jyn ,令
Z
Z
Z 表示观测向量{
z
1
,
.
.
.
,
z
N
z_1,...,z_N
z1,...,zN} ,将
α
\alpha
α表示为待估计参数,则其最大似然函数为:
L
o
(
ω
,
A
,
θ
)
=
−
N
2
(
σ
0
2
+
σ
1
2
)
A
2
+
∑
n
=
1
N
(
x
n
cos
ϕ
n
+
y
n
sin
ϕ
n
)
σ
0
2
+
σ
1
2
A
+
σ
1
2
∑
n
=
1
N
(
x
n
cos
ϕ
n
+
y
n
sin
ϕ
n
)
2
2
σ
0
2
(
σ
0
2
+
σ
1
2
)
+
C
\begin{gathered} L_{\mathfrak{o}}(\omega,A,\theta) =-\frac N{2\Big(\sigma_0^2+\sigma_1^2\Big)}A^2+\frac{\sum_{n=1}^N(x_n\cos\phi_n+y_n\sin\phi_n)}{\sigma_0^2+\sigma_1^2}A+ \frac{\sigma_1^2\sum_{n=1}^N(x_n\cos\phi_n+y_n\sin\phi_n)^2}{2\sigma_0^2\left(\sigma_0^2+\sigma_1^2\right)}+C \end{gathered}
Lo(ω,A,θ)=−2(σ02+σ12)NA2+σ02+σ12∑n=1N(xncosϕn+ynsinϕn)A+2σ02(σ02+σ12)σ12∑n=1N(xncosϕn+ynsinϕn)2+C
对于参数A,是一个二次函数,可以很容易求得其最大似然估计。然而对于参数
ϕ
n
\phi_n
ϕn很直接求得其最大似然估计。
表达式如下:
L
1
(
ω
,
θ
)
=
L
2
(
ω
,
θ
)
+
L
3
(
ω
,
θ
)
L_1(\omega,\theta){=}L_2(\omega,\theta){+}L_3(\omega,\theta)
L1(ω,θ)=L2(ω,θ)+L3(ω,θ)
L 2 ( ω , θ ) = 1 N 2 [ ∑ n = 1 N ( x n cos ϕ n + y n sin ϕ n ) ] 2 L_2\left(\omega,\theta\right)=\frac1{N^2}\left[\sum_{n=1}^N(x_n\cos\phi_n+y_n\sin\phi_n)\right]^2 L2(ω,θ)=N21[n=1∑N(xncosϕn+ynsinϕn)]2
L 3 ( ω , θ ) = N P R 2 N ∑ n = 1 N ( x n cos ϕ n + y n sin ϕ n ) 2 L_3(\omega,\theta)=\frac{\mathbf{NPR}}{2N}\sum_{n=1}^N(x_n\cos\phi_n+y_n\sin\phi_n)^2 L3(ω,θ)=2NNPRn=1∑N(xncosϕn+ynsinϕn)2
4.基于修正傅里叶插值的粗估计
噪声调幅信号频率的估计,其本质是寻找合适频率与相位最大化其DFT结果的峰值。这一模型在指数信号的经典估计模型下,有大量的参数估计方法。但是这些方法忽略了调制噪声中的参数,算法性能恶化。
所以有一直基于修正傅里叶系数插值的参数估计方法,利用调制噪声区别于AWGN的特点,在很大程度上完全消除调制噪声对参数的影响。
(8)基于多步干扰消除的完全转发式干扰抑制技术
密集假目标干扰应具备如下特点:
1.一个脉冲之内的可能有多簇完全转发式的密集假目标干扰;
2.—簇完全转发式密集假目标干扰,具有等间隔转发特性;
3.—簇干扰中的不同假目标,具有大致等功率转发的特性;
4.一簇干扰中的不同假目标,其相位具有线性变化的特点;
实际数据中的完全转发式密集假目标干扰,可以看成是基于DRFM的干扰机以某种较为简单的规律,不断转发其存储的雷达发射波形,且只对每个转发的干扰分量进行最基本的调制处理。
设雷达信号
s
(
t
,
T
)
=
r
e
c
t
(
t
T
e
x
p
(
j
π
K
t
2
)
)
s(t,T)=rect(\frac{t}{T}exp(j\pi Kt^2))
s(t,T)=rect(Ttexp(jπKt2)),干扰信号的数学模型为
J
1
(
t
)
=
∑
p
=
1
M
∑
q
=
1
Q
p
P
1
(
p
,
q
)
s
[
t
−
τ
1
(
p
,
q
)
,
T
]
⋅
e
j
θ
1
(
p
,
q
)
J_1\left(t\right)=\sum_{p=1}^M\sum_{q=1}^{\mathcal{Q}_p}\sqrt{P_1\left(p,q\right)}s{\left[t-\tau_1\left(p,q\right),T\right]}\cdotp e^{j\theta_1\left(p,q\right)}
J1(t)=p=1∑Mq=1∑QpP1(p,q)s[t−τ1(p,q),T]⋅ejθ1(p,q)
这种技术的关键是对每一簇的参数进行估计,但是不同的干扰簇可能会发生交叠,当LFM的密集程度比较高时,交叠会对参数估计产生较大影响。所以考虑多步交叠的干扰消除参数估计方法。其核心思想是先进行DFT变换,然后检测幅度谱上峰值对应的频点,然后通过频点设计滤波器,分离各个LFM分量,然后通过傅里叶系数插值的方法,对各个LFM分量的参数进行粗估计,然后重构各个LFM分量,然后再接收信号中消除其他LFM分量,只保留待估计的LFM分量,然后再对LFM分量进行参数估计。一直把所有LFM分量估计完成。
(9)基于EEMD的部分转发干扰抑制技术
为方便以后查看,将EMD阅读笔记保存到博客上EMD经验模态分解介绍_黑川赤音的博客-CSDN博客
基于EEMD的部分转发式密集假目标干扰的抑制方法如下:
若雷达受到的干扰信号如下:
r
2
(
t
)
=
s
e
(
t
)
+
J
2
(
t
)
+
n
(
t
)
r_2(t)=s_e(t)+J_2(t)+n(t)
r2(t)=se(t)+J2(t)+n(t)
首先对雷达接收到的信号进行去斜处理:
x
(
t
)
=
r
2
(
t
)
e
x
p
(
−
j
K
π
t
2
)
x(t)=r2(t)exp(-jK\pi t^2)
x(t)=r2(t)exp(−jKπt2) ; 然后用EEMD方法对去斜后的信号
x
(
t
)
x(t)
x(t) 进行处理,同一个拼接部分中,比如第
m
m
m段干扰内,所叠加的
Q
m
Q_m
Qm个部分转发式干扰应当被分解到不同的IMF中。对各个IMF函数进行Hilbert-Huang变换处理,瞬时频率在相邻的拼接部分会产生频率跳变现象,干扰时延和其持续的时间,可以通过检测这些调频点来检测:
∃
f
,
∣
∫
t
−
Δ
t
i
Y
(
τ
,
f
)
d
τ
−
∫
t
i
t
i
+
Δ
Y
(
τ
,
f
)
d
τ
∣
∣
∫
t
i
−
Δ
t
i
Y
(
τ
,
f
)
d
τ
+
∫
t
i
t
+
Δ
Y
(
τ
,
f
)
d
τ
∣
≥
1
2
\exists f,\frac{\left|\int_{t-\Delta}^{t_i}Y(\tau,f)d\tau-\int_{t_i}^{t_i+\Delta}Y(\tau,f)d\tau\right|}{\left|\int_{t_i-\Delta}^{t_i}Y(\tau,f)d\tau+\int_{t_i}^{t+\Delta}Y(\tau,f)d\tau\right|}\geq\frac12
∃f,
∫ti−ΔtiY(τ,f)dτ+∫tit+ΔY(τ,f)dτ
∫t−ΔtiY(τ,f)dτ−∫titi+ΔY(τ,f)dτ
≥21
估计方法使用如下方法来估计:
min
τ
j
,
T
m
,
k
∑
i
=
0
N
[
t
i
−
(
τ
2
+
k
⋅
T
m
)
]
2
s
.
t
.
T
=
M
T
m
0
≤
k
≤
M
−
1
M
∈
Z
+
\begin{aligned} &\min_{\tau_{j},T_{m},k} \sum_{i=0}^N[t_i-(\tau_2+k\cdot T_m)]^2 \\ &s.t. T=MT_{m} \\ &0\leq k\leq M-1 \\ &\boldsymbol{M}\in\boldsymbol{\Z}^{+} \end{aligned}
τj,Tm,kmini=0∑N[ti−(τ2+k⋅Tm)]2s.t.T=MTm0≤k≤M−1M∈Z+
估计出干扰之后,在重构干扰,然后在用其抵消,最后就得到了干扰抑制结果。
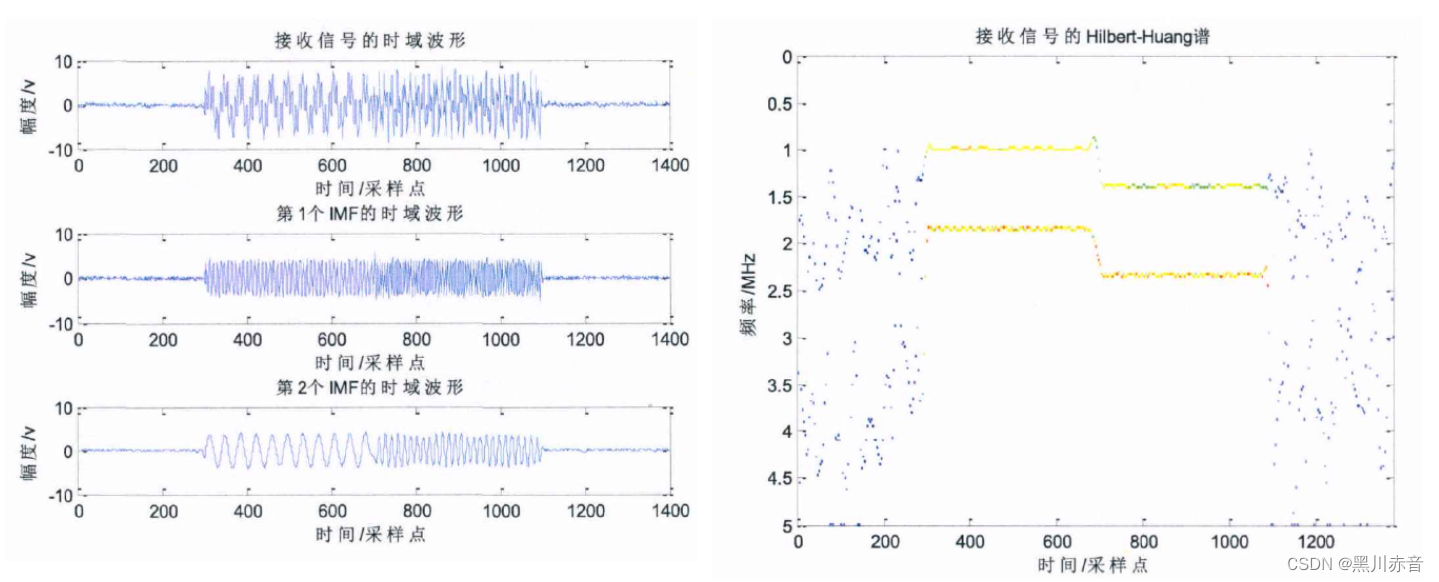
(10)基于时-频域联合处理的卷积式灵巧噪声干扰抑制
信号模型:
通过噪声来调制DRFM所存储的雷达发射信号的副本,可以拥有和真实目标信号高度相参的脉内特性,并使得干扰功率得以充分利用,同时具有欺骗和压制效果:
J
(
t
)
=
P
d
⋅
∑
q
=
1
Q
W
q
s
(
t
−
τ
d
−
τ
q
,
T
)
⋅
exp
[
j
2
π
f
d
(
t
−
τ
d
−
τ
q
)
+
j
ϕ
d
]
J\left(t\right)=\sqrt{P_{d}}\cdot\sum_{q=1}^{Q}W_{q}s\left(t-\tau_{d}-\tau_{q},T\right)\cdot\exp\left[j2\pi f_{d}\left(t-\tau_{d}-\tau_{q}\right)+j\phi_{d}\right]
J(t)=Pd⋅q=1∑QWqs(t−τd−τq,T)⋅exp[j2πfd(t−τd−τq)+jϕd]
P
d
P_d
Pd和
τ
d
\tau_d
τd分别表示卷积式灵巧噪声干扰的功率和处理时延,干扰信号进行了适当的移频
f
d
f_d
fd,以保证PC的处理效果{
W
q
W_q
Wq}是一个均值为零,具有单位方差的离散复高斯白噪声序列。由DRFM干扰机产生,干扰机通过调整时延序列{
τ
d
\tau_d
τd}的大小,以使干扰机表现出不同的特征样式。
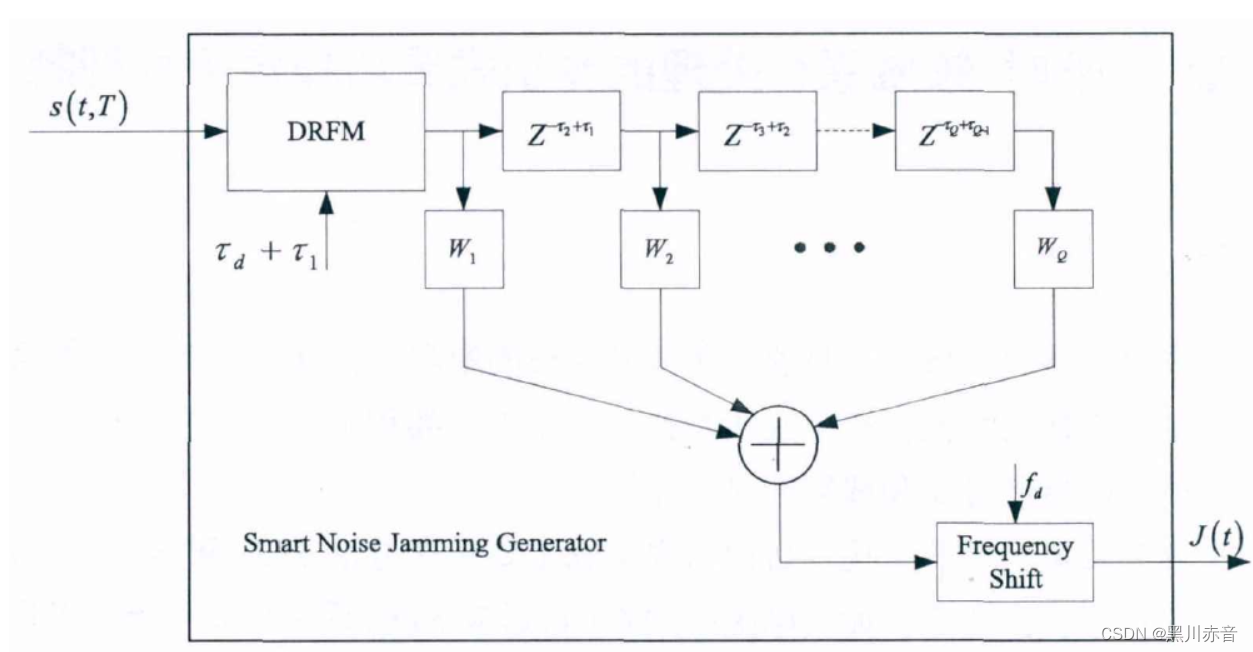
当时延序列较小时,与雷达接收机的目标分辨间隔相比拟时,干扰信号的脉冲压缩结果无法形成假目标串,更多的是表现出一种压制干扰效果。反之,表现出欺骗干扰的效果。
假设真实目标功率远远小于干扰信号功率,真实信号时延小于干扰信号时延。雷达接收到的信号为 r ( t ) = s e ( t ) + J ( t ) + n ( t ) r(t)=s_e(t)+J(t)+n(t) r(t)=se(t)+J(t)+n(t) 。
这种干扰的一个显著特征就是在时间上落后于真时目标回波,但干扰机通过一定的移频处理,利用LFM信号时延与移频相耦合的特性,使得干扰机经过PC处理后能覆盖真实目标。
由于卷积式灵巧噪声干扰的移频量是固定的,是干扰机针对LFM信号的调频斜率添加的。因此,考虑使用SMSP技术来改变LFM信号中的调频斜率,使得干扰机固定的移频量,无法满足干扰PC结果覆盖真实目标的要求。

这样真实目标回波的PC结果不会再被卷积式灵巧噪声所覆盖,从而可以被分辨出来。
卷积式灵巧噪声干扰的脉冲压缩结果如下:
y
(
t
)
=
P
d
e
j
ϕ
d
⋅
(
B
−
f
d
)
exp
(
−
j
π
f
d
2
K
)
⋅
exp
(
−
j
4
π
f
d
τ
d
)
⋅
∑
q
=
1
Q
W
q
s
i
n
c
[
(
B
−
f
d
)
(
t
−
τ
d
−
τ
q
+
f
d
K
)
]
⋅
exp
(
−
j
4
π
f
d
τ
q
)
\begin{aligned} y(t)& =\sqrt{P_d}e^{j\phi_d}\cdot(B-f_d)\exp\left(-j\pi\frac{f_d^2}K\right)\cdotp\exp(-j4\pi f_d\tau_d) \\ &\cdot\sum_{q=1}^QW_q\mathrm{sinc}\bigg[(B-f_d)\bigg(t-\tau_d-\tau_q+\frac{f_d}K\bigg)\bigg]\cdot\exp\left(-j4\pi f_d\tau_q\right) \end{aligned}
y(t)=Pdejϕd⋅(B−fd)exp(−jπKfd2)⋅exp(−j4πfdτd)⋅q=1∑QWqsinc[(B−fd)(t−τd−τq+Kfd)]⋅exp(−j4πfdτq)
可以看出,直接对卷积式灵巧噪声干扰匹配滤波后,第
q
q
q个分量进行CFAR检测的峰值位置位于
τ
d
+
τ
q
−
f
d
/
K
\tau_d+\tau_q-f_d/K
τd+τq−fd/K处。由于干扰的PC结果需要覆盖真实目标,因此,调制的移频量
f
d
f_d
fd应满足:
τ
d
+
τ
1
−
f
d
K
<
τ
e
<
τ
d
+
τ
Q
−
f
d
K
\tau_{d}+\tau_{1}-\frac{f_{d}}{K}<\tau_{e}<\tau_{d}+\tau_{Q}-\frac{f_{d}}{K}
τd+τ1−Kfd<τe<τd+τQ−Kfd
τ
e
\tau_e
τe为真实目标回波的时延。使用SMSP之后,
K
K
K会变为
K
m
K_m
Km,那么CFAR检测到的新的峰值会位于
t
d
=
τ
d
+
τ
q
−
f
d
/
K
m
t_d=\tau_d+\tau_q-f_d/K_m
td=τd+τq−fd/Km处,此时可以得到结论:当利用SMSP方法对卷积式灵巧噪声进行处理后,匹配滤波所形成的假目标峰值位置发生正向偏移。
不断调整
m
m
m的值,一定可以达到
τ
e
<
τ
1
−
f
d
/
M
k
\tau_{e}<\tau_{1}-f_{d}/M_k
τe<τ1−fd/Mk的时候,此时就可以分辨出假目标,然后估计出:
t
^
d
,
q
=
m
⋅
t
d
(
1
,
q
)
−
t
d
(
m
,
q
)
m
−
1
\hat{t}_{d,q}=\frac{m\cdot t_{d}\left(1,q\right)-t_{d}\left(m,q\right)}{m-1}
t^d,q=m−1m⋅td(1,q)−td(m,q)
估计出{
t
d
,
q
t_{d,q}
td,q}后,再用其他方法估计
A
^
q
=
P
d
e
j
ϕ
d
⋅
W
q
\hat{A}_{q}=\sqrt{P_{d}}e^{j\phi_{d}}\cdot W_{q}
A^q=Pdejϕd⋅Wq ,然后就可以对消掉干扰达到抑制干扰的效果。
SMSP和C&I干扰介绍
SMSP和C&I距离假目标欺骗干扰识别和抑制方法研究 2012
SMSP介绍
SMSP干扰是距离假目标新式干扰之一,它由多个子脉冲组成,每个子脉冲都是对雷达信号进行间隔采样产生的,因此可以在雷达接收端产生虚假目标,影响真实目标检测。传统的移频转发干扰由于他只能产生一个假目标导致不能有效的干扰PC雷达,所以SMSP对截取的雷达频率进行调制,产生一连串梳状假目标来欺骗雷达。
(一)干扰过程介绍
脉冲压缩雷达发射线性调频信号,其载频在脉冲内宽度是随时间按线性按线规律变化的 , DRFM接收并储存该信号并在时域上对其采样,假设采样点数为N,那么采样后将时钟频率提高为 n n n倍,对采样数据进行抽取并按原顺序进行排序,然后对排序后的信号复制 n n n次,得到信号的干扰样式,即为SMSP干扰。
由以上干扰可知,其导致了干扰信号与雷达信号含有不同的调频斜率,经过多次重复使得SMSP含有多个结构相同的子脉冲。由于其与雷达的相似结构,使得其可以在雷达输出端产生多瓣。当干扰概率较大时,其具有欺骗和压制的双重作用。
(二)特性机理
- LFM信号: S T ( t ) = e x p ( j π k t 2 ) S_T(t)=exp(j\pi k t^2) ST(t)=exp(jπkt2)
- 高频采样后的脉冲: J 1 ( t ) = e x p ( j π k 1 t 2 ) J_1(t)=exp(j\pi k_1t^2) J1(t)=exp(jπk1t2) k 1 = n k k_1=nk k1=nk
- 复制 n n n次
J S M S P ( t ) = ∑ i = 0 n − 1 J 1 ( t − i T n ) ∗ ∑ i = 0 n − 1 δ ( t − i T n ) J_{SMSP}(t)=\sum_{i=0}^{n-1}J_1(t-i\frac{T}{n}) *\sum_{i=0}^{n-1}\delta(t-i\frac{T}{n}) JSMSP(t)=i=0∑n−1J1(t−inT)∗i=0∑n−1δ(t−inT)
4.假设发射信号的频谱为
S
(
f
)
S(f)
S(f),则干扰信号的频谱为
J
S
M
S
P
(
f
)
=
s
i
n
c
(
f
T
)
n
s
i
n
c
(
f
T
/
n
)
e
−
j
π
(
1
−
1
n
)
T
S
(
f
n
)
J_{SMSP}(f)=\frac{sinc(fT)}{\sqrt{n}sinc(fT/n)}e^{-j\pi(1-\frac{1}{n})T}S(\frac{f}{\sqrt{n}})
JSMSP(f)=nsinc(fT/n)sinc(fT)e−jπ(1−n1)TS(nf)
对应图像如下:
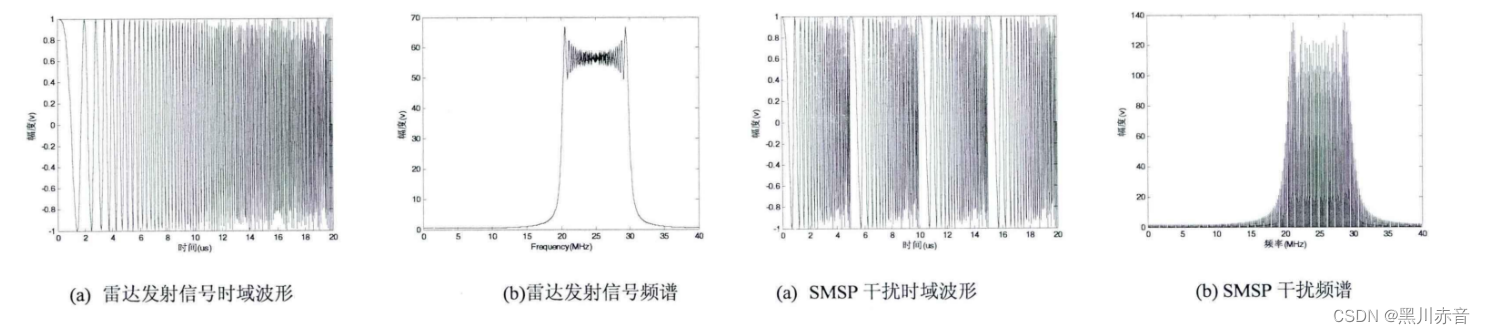
5.经过下变频后,发射信号的瞬时频率为 k t kt kt 而干扰信号的瞬时频率为 n k t ∗ ∑ i = 0 n − 1 δ ( t − i T n ) nkt*\sum_{i=0}^{n-1}\delta(t-i\frac{T}{n}) nkt∗∑i=0n−1δ(t−inT) ,如下:

由于SMSP干扰信号是多个子脉冲信号的叠加,因此其通过匹配滤波器的输出仍然近似为矩形,只是由于多个脉冲叠加的作用,导致其幅度输出比较剧烈。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QkBVxt6N-1691935317867)(C:\Users\张楷煜\AppData\Roaming\Typora\typora-user-images\image-20230731222711255.png)]](https://img-blog.csdnimg.cn/4da4d0559e0d435692f52060015fae27.png)
从上图SMSP干扰通过匹配滤波器可以看出,干扰通过匹配滤波器后,会产生一系列的虚假峰,使雷达无法正常检测到目标,达到了欺骗和压制的双重作用。
以上叙述可以看出:无论是在频域还是在时域,SMSP干扰与雷达信号在时域上和频域上都是重叠的,以下介绍其利用谱图(STFT,通过时域加窗把信号分为许多小的时间段,然后将每一小段信号看为短时平稳信号,再用傅里叶变换对其分析)方法检查二者在时频联合域上的重叠程度。
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9ESNlN52-1691935317867)(C:\Users\张楷煜\AppData\Roaming\Typora\typora-user-images\image-20230801094957387.png)]](https://img-blog.csdnimg.cn/79dabc26cb64410cb655f5a0c455349f.png)
从图上可以看出,显然雷达信号和干扰信号的谱图不一样。
C&I介绍
(一)干扰过程介绍
与SMSP不同的是,其每一段都是对雷达信号的复制。
C&I干扰的产生过程为:(1)Chopping阶段,截取雷达信号不同的段,这些小段都是雷达信号的一部分,且含有不同的时间段和频率分布。(2)Interleaving阶段,将小段信号复制到相邻的间隙中,此时就产生了C&I干扰。其和匹配滤波器是相匹配的,因此可以在雷达接收端产生虚假目标,达到欺骗的效果。
(二)C&I干扰机理介绍
1.chopping阶段
P
(
t
)
=
S
T
(
t
)
a
(
t
)
=
S
T
(
t
)
[
r
e
c
t
(
t
−
τ
a
τ
a
)
∗
∑
i
=
0
m
−
1
δ
(
t
−
i
T
a
)
]
P(t)=S_T(t)a(t)=S_T(t)[rect(\frac{t-\tau_a}{\tau_a})*\sum_{i=0}^{m-1}\delta(t-iT_a)]
P(t)=ST(t)a(t)=ST(t)[rect(τat−τa)∗i=0∑m−1δ(t−iTa)]
a ( t ) a(t) a(t)为矩形脉冲串,脉宽为 T / m n T/mn T/mn ,基波周期为 T a = T / m T_a=T/m Ta=T/m,基波频率为 f a = 1 / T a f_a=1/T_a fa=1/Ta。
2.Interlevaing阶段
J
C
I
(
t
)
=
∑
k
=
0
n
−
1
P
(
t
−
k
T
/
m
n
)
J_{CI}(t)=\sum_{k=0}^{n-1}P(t-kT/mn)
JCI(t)=k=0∑n−1P(t−kT/mn)
C$I干扰的第p个子脉冲的第q个时隙信号的信号模型为:
J
C
I
p
,
q
(
t
)
=
e
x
p
[
j
π
k
(
t
−
q
−
1
m
n
T
)
2
]
J_{CI}^{p,q}(t)=exp[j\pi k(t-\frac{q-1}{mn}T)^2]
JCIp,q(t)=exp[jπk(t−mnq−1T)2]
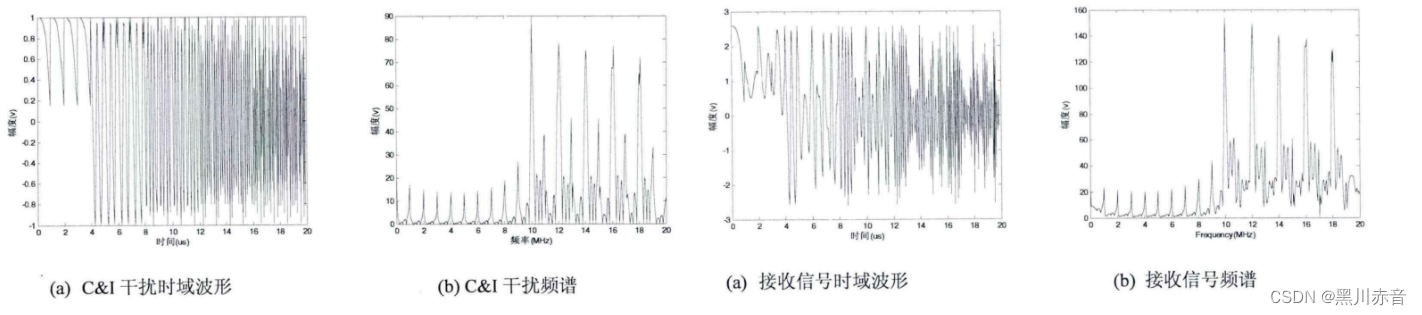
对齐进行傅里叶变换:得到其波形频谱如下:
对
a
(
t
)
a(t)
a(t)使用傅里叶级数展开:
a
(
t
)
=
τ
a
T
a
+
2
τ
a
T
a
∑
r
=
1
inf
s
i
n
π
r
f
s
τ
a
π
r
f
s
τ
a
c
o
s
2
π
r
f
s
t
=
1
n
+
2
n
∑
r
=
1
inf
s
i
n
π
r
/
n
π
r
/
n
c
o
s
2
π
r
f
s
t
a(t)=\frac{\tau_a}{T_a}+\frac{2\tau_a}{T_a}\sum_{r=1}^{\inf} \frac{sin\pi r f_s\tau_a}{\pi r f_s\tau_a}cos2\pi r f_st=\frac{1}{n}+\frac{2}{n}\sum_{r=1}^{\inf} \frac{sin\pi r /n}{\pi r /n}cos2\pi r f_st
a(t)=Taτa+Ta2τar=1∑infπrfsτasinπrfsτacos2πrfst=n1+n2r=1∑infπr/nsinπr/ncos2πrfst
带入
P
(
t
)
P(t)
P(t)为:
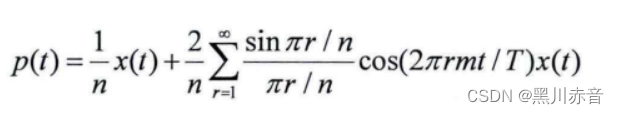
将
P
(
t
)
P(t)
P(t)通过匹配滤波器为:
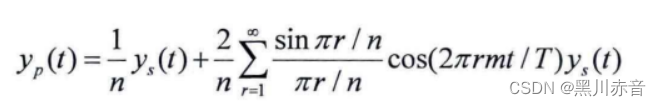
那么结果如下图:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QUT7VdsL-1691935317868)(C:\Users\张楷煜\AppData\Roaming\Typora\typora-user-images\image-20230801110521537.png)]](https://img-blog.csdnimg.cn/f9fed9d0275742a4a346ca5e5fe0e1a0.png)
SMSP和C&I干扰识别
SMSP干扰识别
(一)基于相位的差分识别
首先使用瞬时相位,对瞬时相位做一阶差分即为信号瞬时频率。但是一阶相位差受噪声的影响较大,又有多重相位差分来解决这一问题。识别出频率随时间的变化就可以识别出SMSP干扰。
(二)基于干扰调频斜率的SMSP识别
根据SMSP干扰的产生过程以及信号表达式可以知道,每一个子脉冲为完整的线性调频信号且其调频斜率是 雷达信号 的
n
n
n 倍。利用这一点,有团队提出了匹配信号变换来识别。
M
x
(
ξ
)
(
c
)
=
∫
t
∈
t
0
x
(
t
)
∣
v
(
t
)
∣
e
−
j
2
π
c
ξ
(
t
)
d
t
M_x^{(\xi)}(c)=\int\limits_{t\in t_0}x(t)\sqrt{\left|v(t)\right|}e^{-j2\pi c\xi(t)}dt
Mx(ξ)(c)=t∈t0∫x(t)∣v(t)∣e−j2πcξ(t)dt
其中
x
(
t
)
x(t)
x(t)为待处理信号,
c
c
c为调频斜率。
ξ
(
t
)
\xi(t)
ξ(t) 为非线性单调相位核函数
v
(
t
)
=
d
ξ
(
t
)
/
d
t
v(t)=d\xi(t)/dt
v(t)=dξ(t)/dt当 待 处理信号 是线性调 频信号 时 , 该变换的实质是将待处理信号分离成无穷多个不同调频斜率信号的叠加 。当待处理信号的相 位函 数与变换所釆用的基函数的相位函数相 匹配时,信号在变换域呈现一个峰值。
该变换的本质是分离出不同的调频斜率。
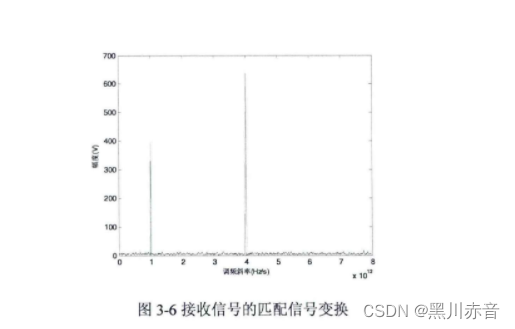
如图所示,有两个尖峰,一个由干扰产生,一个由目标产生。因此,可以用于干扰信号的识别和参数估计。精确识别出干扰的调频斜率后,就可以构造相应的匹配滤波器进行克制。
![[gdc]Rendering ‘God of War Ragnark‘](https://img-blog.csdnimg.cn/5853c2ffba3648c390d61d83b8010a2e.png)
![[鹤城杯 2021]Middle magic 解题思路过程](https://img-blog.csdnimg.cn/83c7317d5cfe49d28b1a8bed774c6c4c.png)