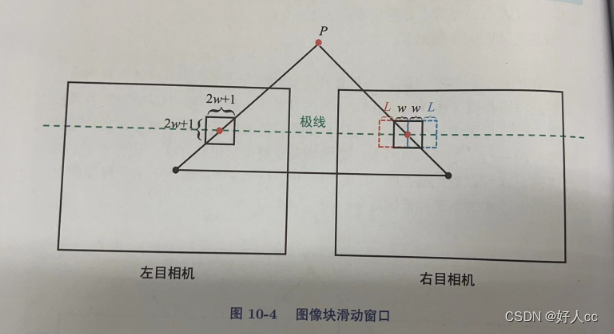
判断时间序列数据是否为平稳时间序列或非平稳时间序列，通常可以通过以下方法：

（1）观察时间序列数据的均值和方差是否随时间变化而发生明显的改变。若均值和方差变化明显，则该时间序列数据可能为非平稳时间序列，反之，则可能为平稳时间序列。

（2）对时间序列数据进行差分后，再对数据通过ADF单位根检验或KPSS检验，如果数据平稳，则该时间序列数据可能为非平稳时间序列，反之，则可能为平稳时间序列。

• 在ADF单位根检验：检验结果包括ADF统计量、p值以及临界值。若 p 值小于显著性水平（常见使用的是0.05），则可以拒绝原假设，即数据是平稳的，反之。
• 在KPSS检验中：检验结果包括KPSS统计量、p值以及临界值。若 p 值小于显著性水平，则可以拒绝原假设，即数据是非平稳的，反之。

为什么先差分再检验平稳性？

• 大部分经典时间序列模型，如ARIMA模型，要求时间序列是平稳的。只有当时间序列平稳时，才能有效运用这些模型来进行预测和建模。
• 差分操作可以去除时间序列中的趋势、季节性等非平稳性因素，使得原始数据更符合平稳性的要求。
• 差分操作可以消除时间序列的自相关性，使得之后的模型拟合和预测更加准确可靠。

2 代码实现

（1）ADF单位根检验示例代码：

from statsmodels.tsa.stattools import adfuller

# data为时间序列数据
result = adfuller(data)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[4].items():
    print('\t%s: %.3f' % (key, value))

（2）KPSS检验示例代码：

from statsmodels.tsa.stattools import kpss

# data为时间序列数据
result = kpss(data)
print('KPSS Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value in result[3].items():
    print('\t%s: %.3f' % (key, value))

（3）差分操作示例代码：

import pandas as pd

# data为时间序列数据，n为差分次数，默认为1
def difference(data, n=1):
    diff = data.diff(n)
    diff.dropna(inplace=True)
    return diff

# 差分1次
diff_data = difference(data)
# 差分2次
diff_data2 = difference(data, n=2)