1. 逻辑回归

逻辑回归（Logistic Regression）的模型是一个非线性模型，

sigmoid函数，又称逻辑回归函数。但是它本质上又是一个线性回归模型，因为除去sigmoid映射函

数关系，其他的步骤，算法都是线性回归的。

可以说，逻辑回归，都是以线性回归为理论支持的。

只不过，线性模型，无法做到sigmoid的非线性形式，sigmoid可以轻松处理0／1分类问题。

       首先，找一个合适的预测函数，一般表示为h函数，该函数就是需要找的分类函数，它用来预

测输入数据的判断结果。然后，构造一个Cost函数（损失函数），该函数表示预测的输出（h）与

训练数据类别（y）之间的偏差，可以是二者之间的差（h—y）或者是其他的形式。综合考虑所有

训练数据的“损失”，将Cost求和或者求平均，记为J（θ）函数，表示所有训练数据预测值与实际类

别的偏差。显然，J（θ）函数的值越小表示预测函数越准确（即h函数越准确），所以这一步需要

做的是找到J（θ）函数的最小值。找函数的最小值有不同的方法，Logistic Regression实现时有的

是梯度下降法（Gradient Descent )。

2. 二分类问题

二分类问题是指预测的y值只有两个取值（0或1），二分类问题可以扩展到多分类问题。例如：我

们要做一个垃圾邮件过滤系统，x是邮件的特征，预测的y值就是邮件的类别，是垃圾邮件还是正常

邮件。对于类别我们通常称为正类（positive class）和负类（negative class），垃圾邮件的例子

中，正类就是正常邮件，负类就是垃圾邮件。

应用举例：是否垃圾邮件分类？是否肿瘤、癌症诊断？是否金融欺诈？

3. logistic函数

如果忽略二分类问题中y的取值是一个离散的取值（0或1），我们继续使用线性回归来预测y的取

值。这样做会导致y的取值并不为0或1。逻辑回归使用一个函数来归一化y值，使y的取值在区间

（0，1）内，这个函数称为Logistic函数（logistic function），也称为Sigmoid函数（sigmoid

function）。函数公式如下：

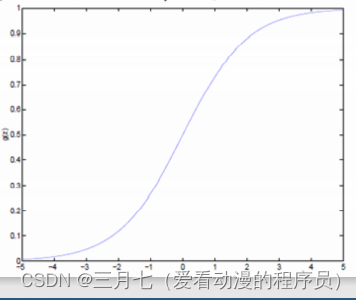
Logistic函数当z趋近于无穷大时，g（z）趋近于1；当z趋近于无穷小时，g（z）趋近于0。Logistic

函数的图形如下：

线性回归模型帮助我们用最简单的线性方程实现了对数据的拟合，然而，这只能完成回归任务，无

法完成分类任务，那么 logistics regression 就是在线性回归的基础上添砖加瓦，构建出了一种分类

模型。如果在线性模型的基础上做分类，比如二分类任务，即：y取值{0，1}，

最直观的，可以将线性模型的输出值再套上一个函数y = g（z），最简单的就是“单位阶跃函数”

（unit—step function），如下图中红色线段所示。

也就是把看作为一个分割线，大于 z 的判定为类别0，小于 z 的判定为类别1。

但是，这样的分段函数数学性质不太好，它既不连续也不可微。通常在做优化任务时，目标函数最

好是连续可微的。这里就用到了对数几率函数（形状如图中黑色曲线所示）。

它是一种"Sigmoid”函数，Sigmoid函数这个名词是表示形式S形的函数，对数几率函数就是其中最

重要的代表。这个函数相比前面的分段函数，具有非常好的数学性质，其主要优势如下：使用该函

数做分类问题时，不仅可以预测出类别，还能够得到近似概率预测。这点对很多需要利用概率辅助

决策的任务很有用。对数几率函数是任意阶可导函数，它有着很好的数学性质，很多数值优化算法

都可以直接用于求取最优解。

总的来说，模型的完全形式如下：，LR模型就是在拟合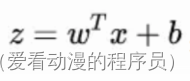

这条直线，使得这条直线尽可能地将原始数据中的两个类别正确的划分开。

对于线性边界的情况，边界形式如下：

构造预测函数为:

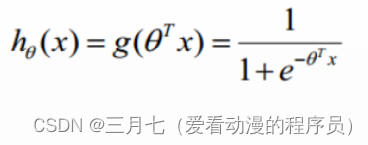
h(x)的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分

别为：

正例(y=1)   

负例(y=0)   

4. 损失函数

对于任何机器学习问题，都需要先明确损失函数，LR模型也不例外，在遇到回归问题时，通常我

们会直接想到如下的损失函数形式（平均误差平方损失MSE)：

但在LR模型要解决的二分类问题中，损失函数的形式是这样的：

这个损失函数通常称作为对数损失(logloss),这里的对数底为自然对数e，其中真实值 y 是有 0/1 两

种情况，而推测值由于借助对数几率函数，其输出是介于0~1之间连续概率值。仔细查看，不难发

现，当真实值y=0时，第一项为0，当真实值y=1时，第二项为0，所以，这个损失函数其实在每次

计算时永远都只有一项在发挥作用，那这就可以转换为分段函数，分段的形式如下：

5. 优化求解 

现在我们已经确定了模型的损失函数，那么接下来就是根据这个损失函数，不断优化模型参数从而

获得拟合数据的最佳模型。

重新看一下损失函数，其本质上是 L 关于模型中线性方程部分的两个参数 w 和 b 的函数：

 其中，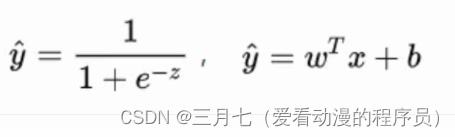

现在的学习任务转化为数学优化的形式即为：

由于损失函数连续可微，我们可以借助梯度下降法进行优化求解，对于两个核心参数的更新方式如

下： 

求得：

进而求得：

转换为矩阵的计算方式为：

至此， Logistic Regression模型的优化过程介绍完毕。

6. 梯度下降算法

梯度下降法求J（θ）的最小值，θ的更新过程：

要使得最大化，则运用梯度上升法，求出最高点：

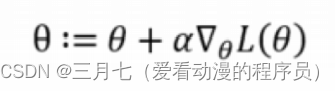
# 梯度上升，主要是采用了最大似然的推导
def gradAscent(dataMatIn,classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)  # n=3
    alpha=0.001  # 学习率
    maxCycles=500  # 循环轮数
    theta = ones((n,1))
    for k in range(maxCycles):
        h=sigmoid(dataMatrix * theta)
        error = (labelMat - h)
        theta = theta + alpha * dataMatrix.transpose()*error
    return theta