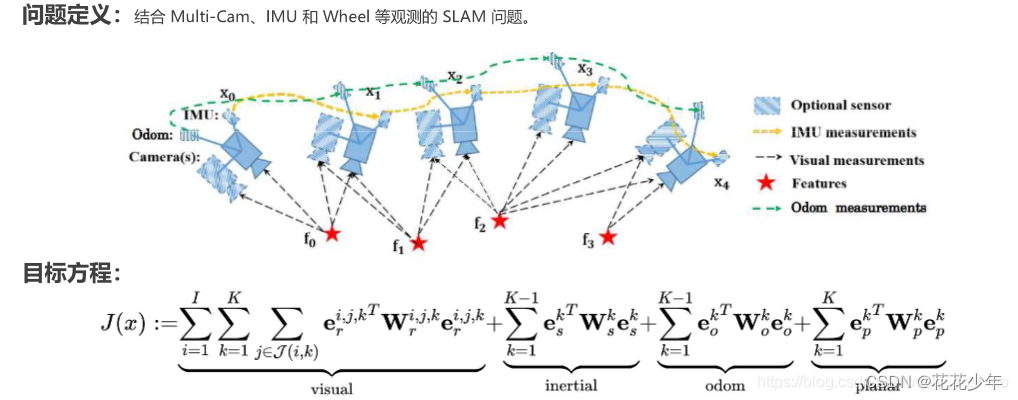
题目

给定一个全是正数的数组arr，定义一下arr的最小不可组成和的概念：

1. arr的所有非空子集中，把每个子集内的所有元素加起来会出现很多的值，其中最小的记为min，最大的记为max；
2. 在区间[min,max]上，如果有一些正数不可以被arr某一个子集相加得到，那么这些正数中最小的那个，就是arr的最小不可组成和；
3. 在区间[min,max]上，如果所有的数都可以被arr的某一个子集相加得到，那么max+1是arr的最小不可组成和。

举例：

• arr = {3,2,5} arr的min为2，max为10，在区间[2,10]上，4是不能被任何一个子集相加得到的值中最小的，所以4是arr的最小不可组成和；
• arr = {3,2,4} arr的min为2，max为9，在区间[2,9]上，8是不能被任何一个子集相加得到的值中最小的，所以8是arr的最小不可组成和；
• arr = {3,1,2} arr的min为1，max为6，在区间[1,6]上，任何数都可以被某一个子集相加得到，所以7是arr的最小不可组成和；

请写函数返回arr的最小不可组成和。

---

思路：动态规划-01背包模型

将上述结论反过来：

---

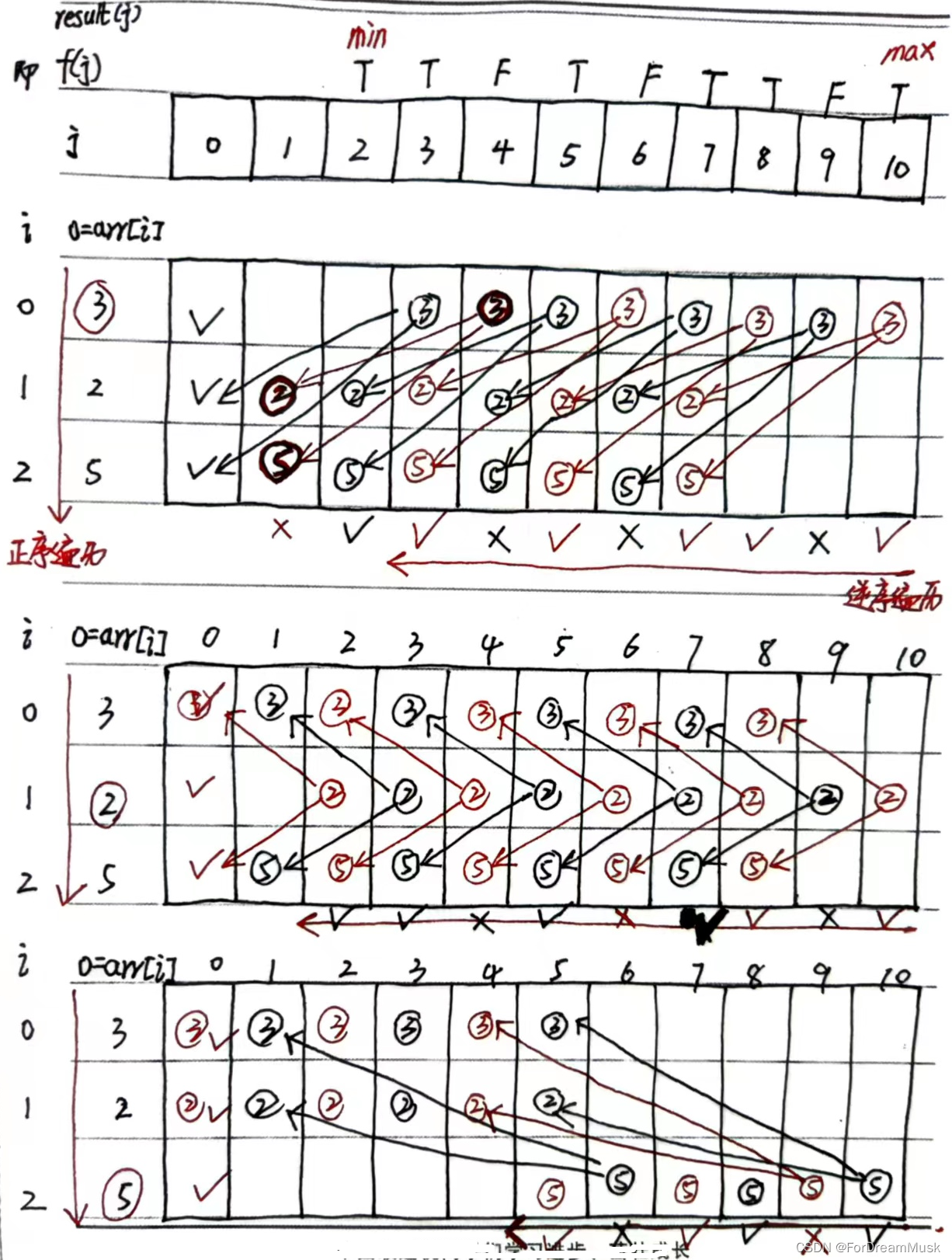
代码

import java.util.*;

public class Solution {
	/**
	 *	正数数组中的最小不可组成和
	 *	输入：正数数组arr
	 *	返回：正数数组中的最小不可组成和
	 */
	public int getFirstUnFormedNum(int[] arr) {
		//得到最小、最大值
		int min = Integer.MAX_VALUE;
		int max = 0;
		for(int i : arr) {
			min = Math.min(min, i);
			max += i;
		}

		//1.创建dp表
		boolean[] result = new boolean[max + 1];

		//2.初始化
		result[0] = true;

		//3.填表
		for(int o : arr) {
			for(int j = max; j >= o; j--) {
				result[j] = result[j - o] || result[j];
			}
		}

		//4.返回值
		for(int j = min; j < result.length; j++) {
			if(!result[j]) {
				return j;
			}
		}
		return max + 1;
	}
}