文章目录
- 前言
- 相关代码整理:
- 介绍
- Minimum Snap Optimization
- Differential Flatness(微分平坦)
- Minimum-snap
- Smooth 1D Trajectory
- Smooth Multi-Segment Trajectory
- Optimization-based Trajectory Generation
- Convex Optimization(凸优化)
- 凸函数和凸集
- 凸优化问题的标准形式
- Linear Programming (LP):线性规划问题
- Quadratic Programming (QP):二次规划问题
- Quadratically Constrained QP (QCQP):具有二次约束的二次规划问题
- Second-Order Cone Programming (SOCP):二阶最优化问题
- Semidefinite Programming(SDP)
- Closed-form Solution to Minimum Snap
- Decision variable mapping变量映射
- Fixed and free variable separation固定变量和自由变量分解
- Hierarchical approach
- Problem: safety issue
- 更好的方案?
- Implementation Details(实现细节)
- Convex Solvers
- Numerical Stability
- Other engineering stuff
- Time Allocation时间分配
- 参考
前言
本文部分内容参考了深蓝学院的移动机器人运动规划,依此做相关的笔记与整理。
相关代码整理:
- https://gitee.com/lxyclara/motion-plan-homework/
- https://github.com/KailinTong/Motion-Planning-for-Mobile-Robots/blob/master
- https://gitee.com/aries-wu/Motion-plan/blob/main/
- 链接: https://pan.baidu.com/s/1UtVHRxDq771LfSGK_21wgQ?pwd=rhtp 提取码: rhtp
介绍
机器人、无人车经历的轨迹需要满足光滑的特征,同时要符合相应的动力学约束。传统的学院派路线很明显需要在产生路径后生成优化后的轨迹以符合kinodynamic的特征;而已经进行过kinodynamic的路径需要进一步优化轨迹以提高路径的质量。
光滑的轨迹生成通常需要符合以下几点特征:
- 边界条件:起点、终点的位置(方向等等)
- 中间条件:中继节点的位置、方向……
- 光滑的轨迹判断标准:评价函数要合理(比如 lim x → x 0 + f ( x ) = lim x → x 0 − f ( x ) \begin{aligned}\lim_{x\rightarrow x_0^+ }f(x)\end{aligned} =\begin{aligned}\lim_{x\rightarrow x_0^- }f(x)\end{aligned} x→x0+limf(x)=x→x0−limf(x))
Minimum Snap Optimization
Differential Flatness(微分平坦)
论文:Minimum Snap Trajectory Generation and Control for Quadrotors, Daniel Mellinger and Vijay Kumar
将全维的状态空间问题
X
X
X转到平坦的空间
σ
\sigma
σ中进行研究。

四旋翼无人机的状态空间
X
X
X由位置、方向、线速度、角速度组成:
X
=
[
x
,
y
,
z
,
ϕ
,
θ
,
ψ
,
x
˙
,
y
˙
,
z
˙
,
ω
x
,
ω
y
,
ω
z
]
T
X=[x,y,z,\phi,\theta,\psi,\dot{x},\dot{y},\dot{z},\omega_x,\omega_y,\omega_z]^T
X=[x,y,z,ϕ,θ,ψ,x˙,y˙,z˙,ωx,ωy,ωz]T角速度是在无人机自身坐标系下观测。
四旋翼的状态和输入可以表示为四个平坦空间里的输出变量及其导数的代数函数。
平坦空间中的任何光滑的轨迹(拥有合理的有界导数)可以被欠驱动系统四旋翼跟踪。
在12维的状态空间中选择4维作为平坦空间:
σ
=
[
x
,
y
,
z
,
ψ
]
T
\sigma=[x,y,z,\psi]^T
σ=[x,y,z,ψ]T
在
T
0
→
T
M
T_0\rightarrow T_M
T0→TM时刻,在平坦空间中的轨迹定义为:
R
3
×
S
O
(
2
)
\mathbb{R}^3\times SO(2)
R3×SO(2)(
R
3
\mathbb{R}^3
R3即为
x
,
y
,
z
,
x,y,z,
x,y,z,
S
O
(
2
)
SO(2)
SO(2)为
ψ
\psi
ψ)
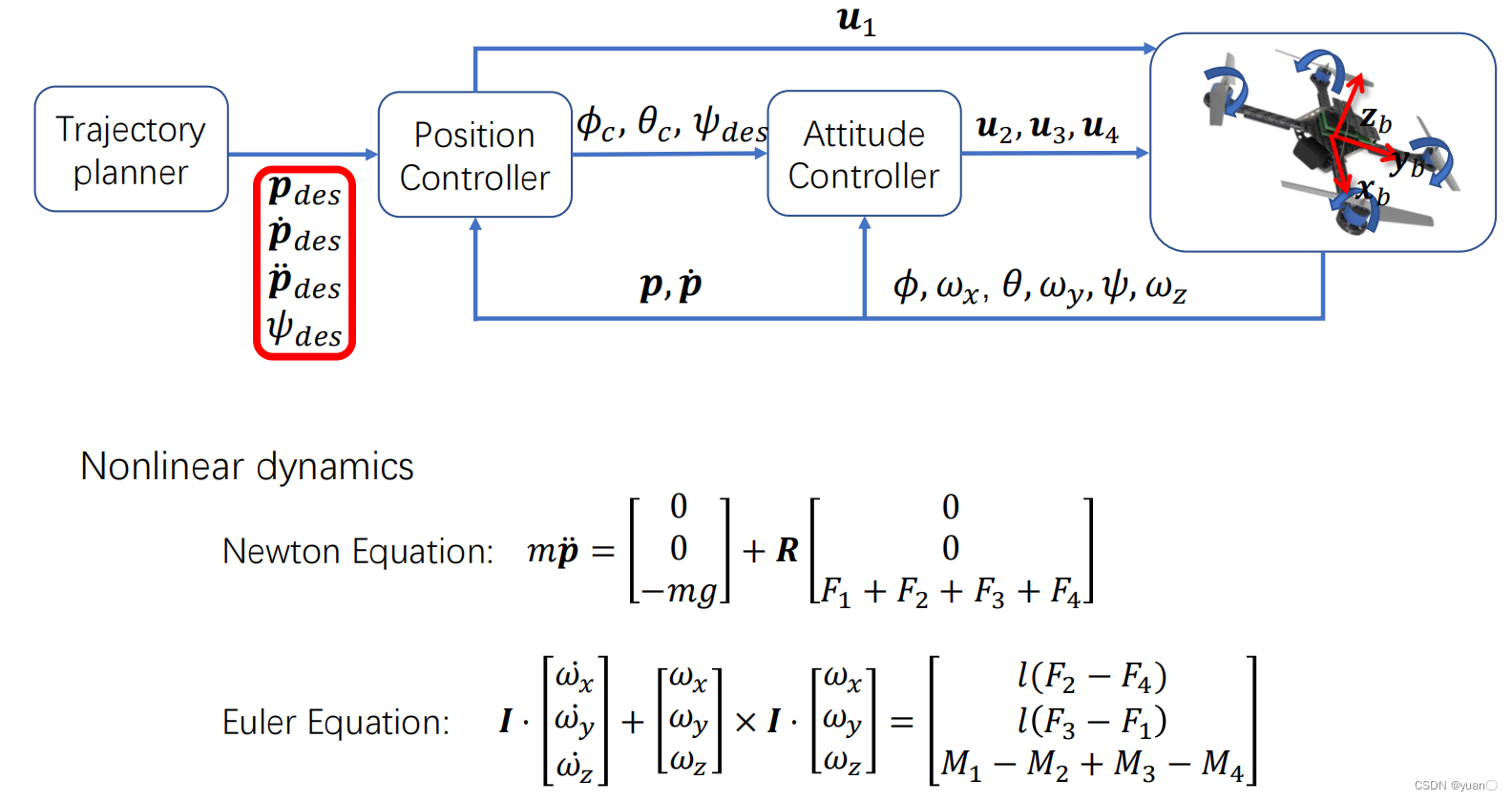
四旋翼无人机的动力学如下所示,分为两个公式:

z
W
\mathbf{z}_W
zW代表了世界坐标系下的
z
\mathbf{z}
z轴,
z
B
\mathbf{z}_B
zB代表了Body坐标系下的
z
\mathbf{z}
z轴。
 从运动等式中可以得到:
z
B
=
t
∥
t
∥
,
t
=
[
σ
¨
1
,
σ
¨
2
,
σ
¨
3
+
g
]
T
\mathbf{z}_B=\dfrac{\mathbf{t}}{\|\mathbf{t}\|},\mathbf{t}=[\ddot{\sigma}_1,\ddot{\sigma}_2,\ddot{\sigma}_3+g]^T
zB=∥t∥t,t=[σ¨1,σ¨2,σ¨3+g]T
σ
1
,
σ
2
,
σ
3
\sigma_1,\sigma_2,\sigma_3
σ1,σ2,σ3分别对于
x
,
y
,
z
x,y,z
x,y,z,因此
t
\mathbf{t}
t代表了无人机合加速度的方向。因此,表示了
z
B
\mathbf{z}_B
zB是
σ
\sigma
σ的变量代数组合。无人机的姿态可以用
x
B
,
y
B
,
z
B
\mathbf{x}_B,\mathbf{y}_B,\mathbf{z}_B
xB,yB,zB进行表示,若能确定
x
B
,
y
B
,
z
B
\mathbf{x}_B,\mathbf{y}_B,\mathbf{z}_B
xB,yB,zB由代数组合,则
ϕ
,
θ
,
ψ
\phi,\theta,\psi
ϕ,θ,ψ也能确定。
从运动等式中可以得到:
z
B
=
t
∥
t
∥
,
t
=
[
σ
¨
1
,
σ
¨
2
,
σ
¨
3
+
g
]
T
\mathbf{z}_B=\dfrac{\mathbf{t}}{\|\mathbf{t}\|},\mathbf{t}=[\ddot{\sigma}_1,\ddot{\sigma}_2,\ddot{\sigma}_3+g]^T
zB=∥t∥t,t=[σ¨1,σ¨2,σ¨3+g]T
σ
1
,
σ
2
,
σ
3
\sigma_1,\sigma_2,\sigma_3
σ1,σ2,σ3分别对于
x
,
y
,
z
x,y,z
x,y,z,因此
t
\mathbf{t}
t代表了无人机合加速度的方向。因此,表示了
z
B
\mathbf{z}_B
zB是
σ
\sigma
σ的变量代数组合。无人机的姿态可以用
x
B
,
y
B
,
z
B
\mathbf{x}_B,\mathbf{y}_B,\mathbf{z}_B
xB,yB,zB进行表示,若能确定
x
B
,
y
B
,
z
B
\mathbf{x}_B,\mathbf{y}_B,\mathbf{z}_B
xB,yB,zB由代数组合,则
ϕ
,
θ
,
ψ
\phi,\theta,\psi
ϕ,θ,ψ也能确定。
接下来定义一个中间坐标系
C
C
C,与world系只差了一个偏航角。
x
C
=
[
cos
σ
4
,
sin
σ
4
,
0
]
T
\mathbf{x}_C=[\cos\boldsymbol{\sigma}_4,\sin\boldsymbol{\sigma}_4,0]^T
xC=[cosσ4,sinσ4,0]T

用
x
C
\mathbf{x}_C
xC叉乘
z
B
\mathbf{z}_B
zB可得
y
B
\mathbf{y}_B
yB
y
B
=
z
B
×
x
C
∥
z
B
×
x
C
∥
,
x
B
=
y
B
×
z
B
R
B
=
[
x
B
y
B
z
B
]
\mathbf{y}_B=\frac{\mathbf{z}_B\times\mathbf{x}_C}{\|\mathbf{z}_B\times\mathbf{x}_C\|},\quad\mathbf{x}_B=\mathbf{y}_B\times\mathbf{z}_B\quad\mathbf{R}_B=\begin{bmatrix}\mathbf{x}_B&\mathbf{y}_B&\mathbf{z}_B\end{bmatrix}
yB=∥zB×xC∥zB×xC,xB=yB×zBRB=[xByBzB]
到此,只剩下角速度部分了。
对
m
p
¨
=
−
m
g
z
W
+
u
1
z
B
m\ddot{\boldsymbol{p}}=-mg\mathbf{z}_W+u_1\mathbf{z}_B
mp¨=−mgzW+u1zB求导,得
m
a
˙
=
u
˙
1
z
B
+
(
ω
B
W
)
×
u
1
z
B
m\dot{\boldsymbol{a}}=\dot{u}_1\mathbf{z}_B+(\boldsymbol{\omega}_{BW})\times u_1\mathbf{z}_B
ma˙=u˙1zB+(ωBW)×u1zB(这里涉及到刚体运动学的一些知识)
B
W
BW
BW:Body angular velocity
viewed in the world frame
因为无人机只受到垂直方向的推力,则
u
˙
1
=
z
B
⋅
m
a
˙
\dot{u}_1=\mathbf{z}_B\cdot m\dot{\boldsymbol{a}}
u˙1=zB⋅ma˙
定义一个
h
ω
\mathbf{h}_\omega
hω,
h
ω
=
ω
B
W
×
z
B
=
m
u
1
(
a
˙
−
(
z
B
⋅
a
˙
)
z
B
)
\mathbf{h}_\omega=\boldsymbol{\omega}_{BW}\times\mathbf{z}_B=\frac m{u_1}(\dot{\boldsymbol{a}}-(\mathbf{z}_B\cdot\dot{\boldsymbol{a}})\mathbf{z}_B)
hω=ωBW×zB=u1m(a˙−(zB⋅a˙)zB)。
h
ω
\mathbf{h}_\omega
hω中的量都可以用平坦空间中表示。
我们知道,
ω
B
W
=
ω
x
x
B
+
ω
y
y
B
+
ω
z
z
B
\omega_{BW}=\omega_x\mathbf{x}_B+\omega_y\mathbf{y}_B+\omega_z\mathbf{z}_B
ωBW=ωxxB+ωyyB+ωzzB
沿
y
B
\mathbf{y}_B
yB、
x
B
\mathbf{x}_B
xB的角速度可以被表示为:
ω
x
=
−
h
ω
⋅
y
B
,
ω
y
=
h
ω
⋅
x
B
\omega_x=-\mathbf{h}_\omega\cdot\mathbf{y}_B,\quad\omega_y=\mathbf{h}_\omega\cdot\mathbf{x}_B
ωx=−hω⋅yB,ωy=hω⋅xB
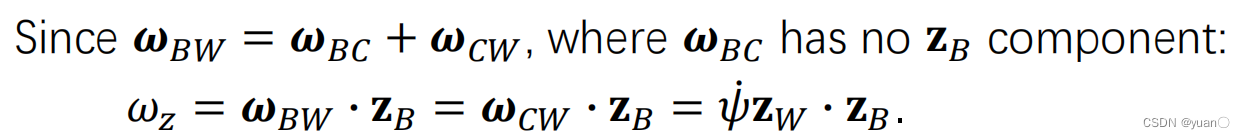
总结

生成的轨迹是一个多项式,其有以下优点:
•使用多项式阶数轻松确定平滑度标准
•导数的简单闭合形式计算
•三维解耦轨迹生成
Minimum-snap
Smooth 1D Trajectory

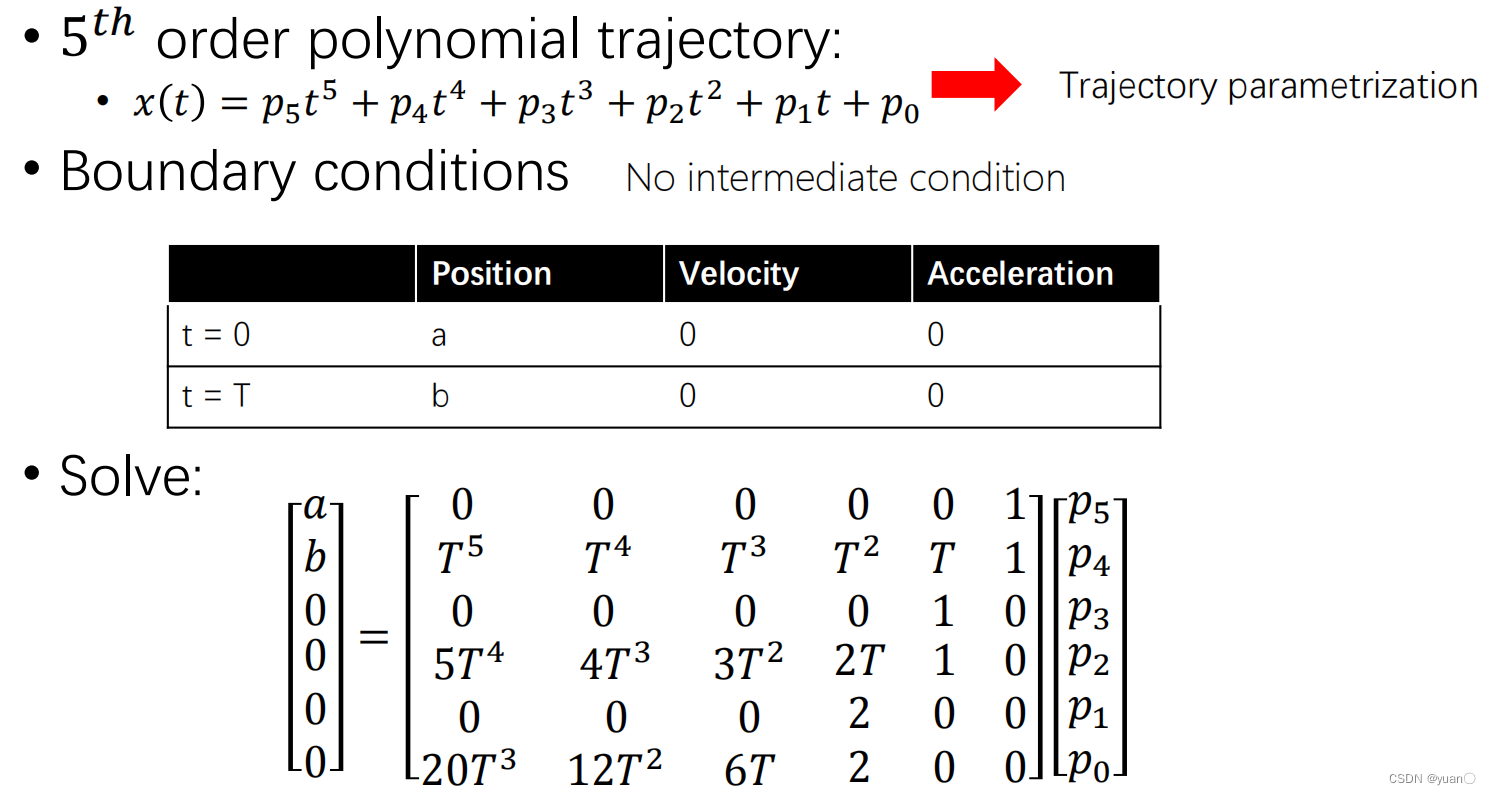
Smooth Multi-Segment Trajectory
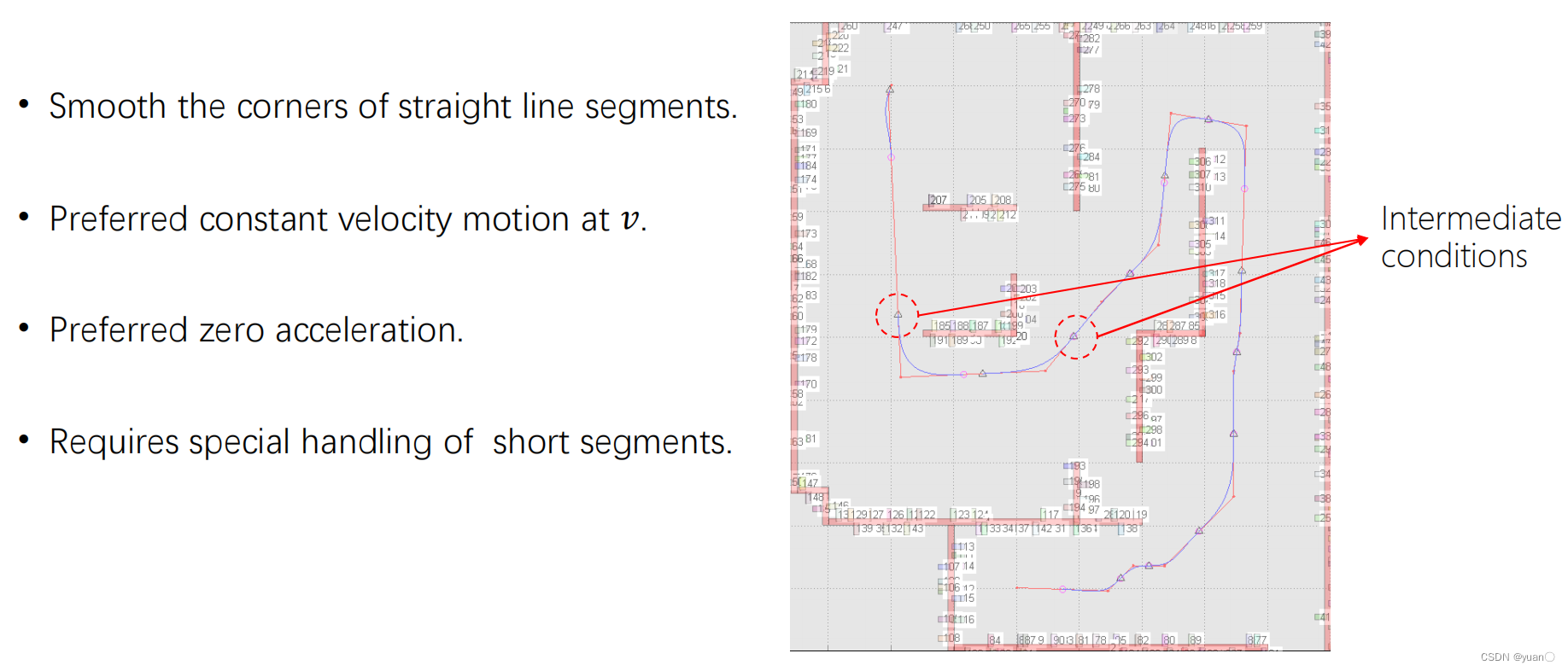

达到这些点的速度和加速度其实是不好指定的。
Optimization-based Trajectory Generation
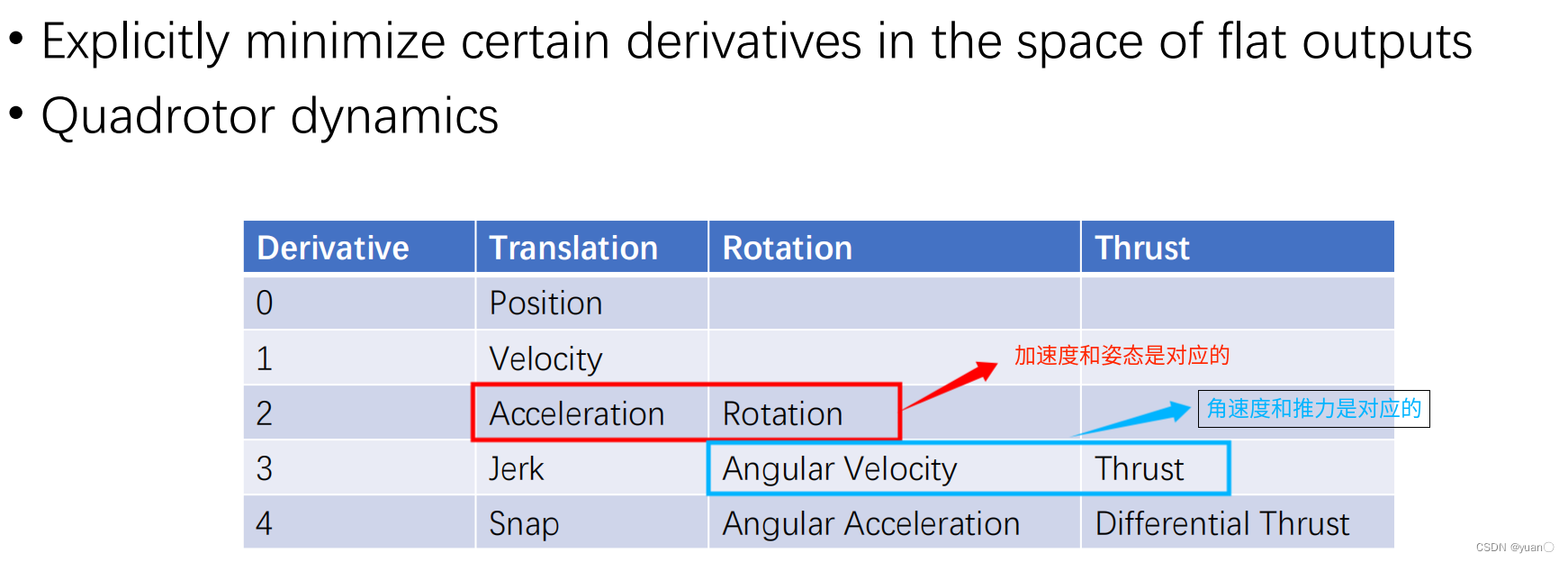
最小化jerk相当于最小角速度,可以获得较好的视觉跟踪视野
最小化snap可以节省能量
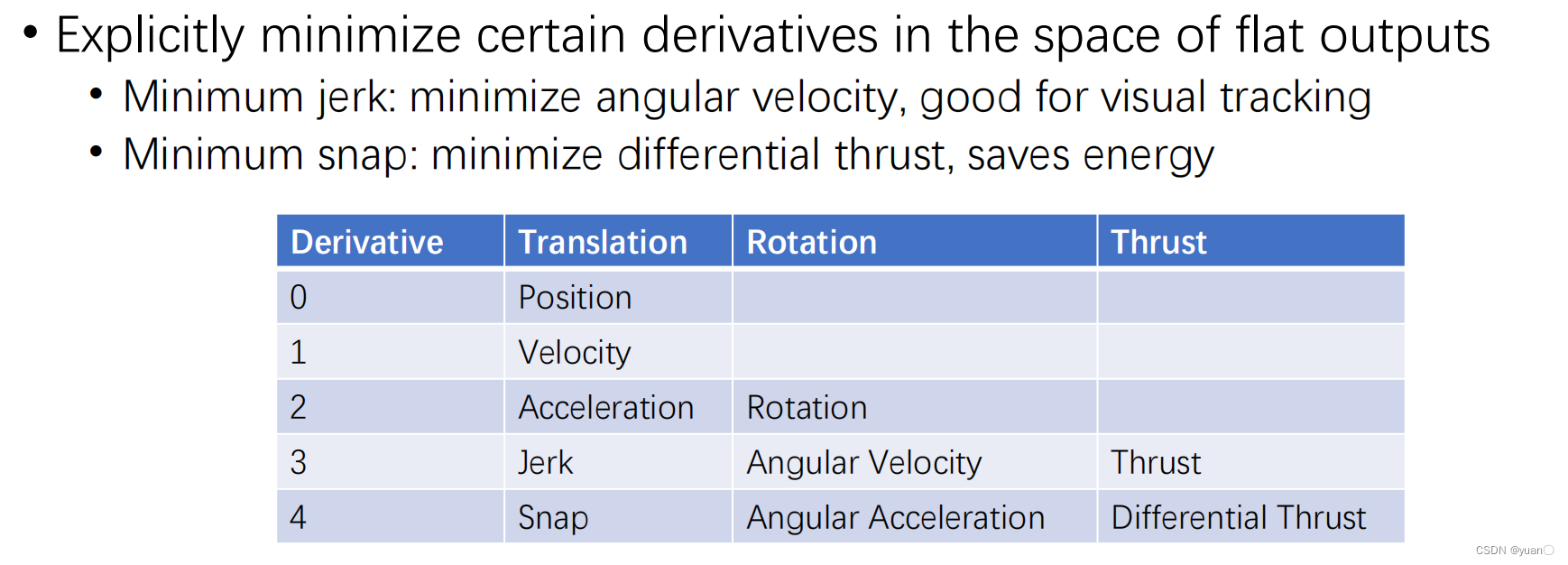
得到以下公式
f
(
t
)
=
{
f
1
(
t
)
≐
∑
i
=
0
N
p
1
,
i
t
i
T
0
≤
t
≤
T
1
f
2
(
t
)
≐
∑
i
=
0
N
p
2
,
i
t
i
T
1
≤
t
≤
T
2
⋮
⋮
f
M
(
t
)
≐
∑
i
=
0
N
p
M
,
i
t
i
T
M
−
1
≤
t
≤
T
M
f(t)=\begin{cases}f_1(t)\doteq\sum_{i=0}^Np_{1,i}t^i&\quad T_0\leq t\leq T_1\\f_2(t)\doteq\sum_{i=0}^Np_{2,i}t^i&\quad T_1\leq t\leq T_2\\\vdots&\quad\vdots\\f_M(t)\doteq\sum_{i=0}^Np_{M,i}t^i&\quad T_{M-1}\leq t\leq T_M\end{cases}
f(t)=⎩
⎨
⎧f1(t)≐∑i=0Np1,itif2(t)≐∑i=0Np2,iti⋮fM(t)≐∑i=0NpM,itiT0≤t≤T1T1≤t≤T2⋮TM−1≤t≤TM
- 每一段都是多项式
- 不一定要求每一段轨迹的阶数是一样的,但一样的可以使问题简化。
- 每一段轨迹的时间需要已知
约束:
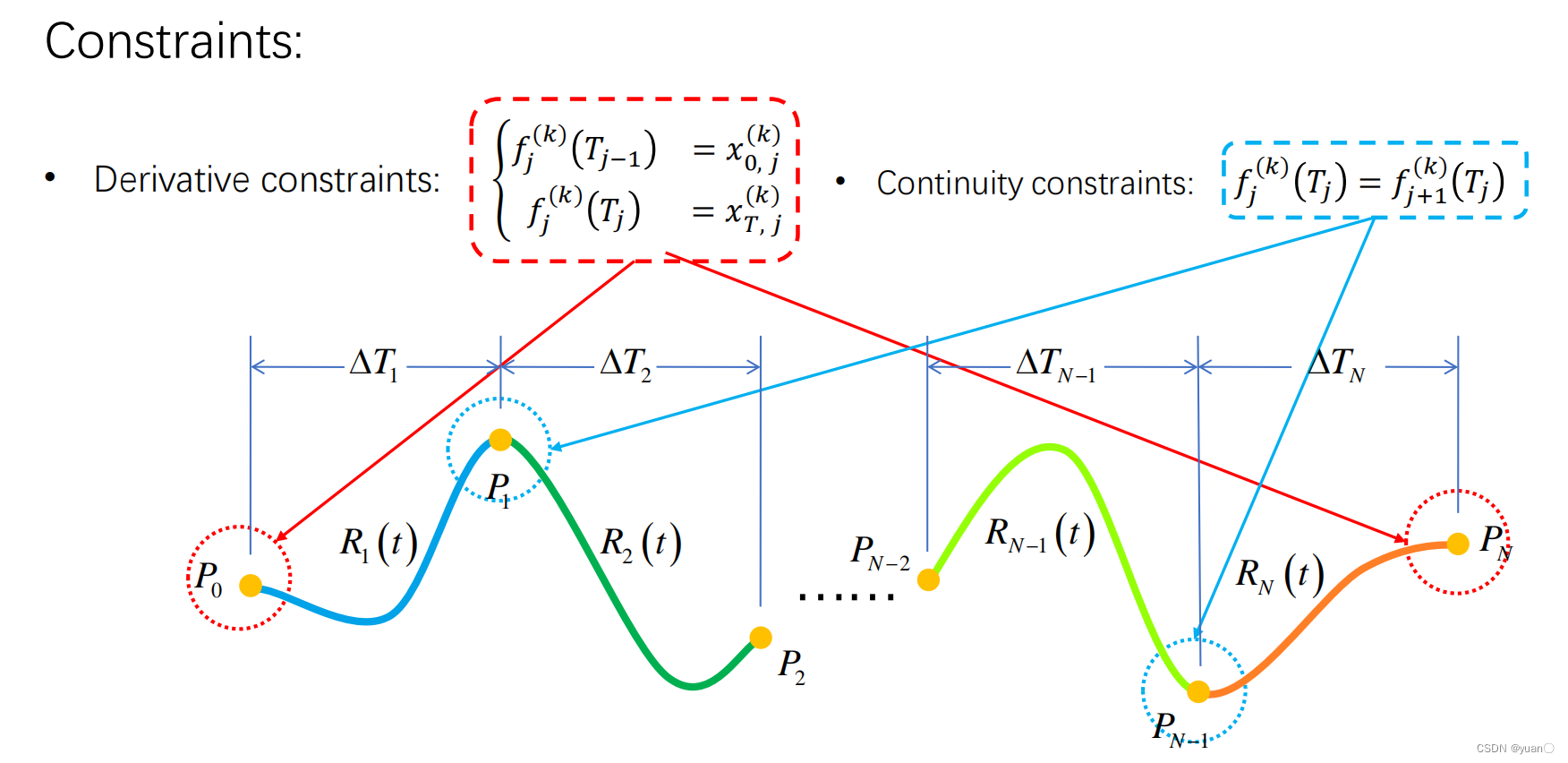
轨迹光滑、连续以及控制输入最小化是彼此独立的
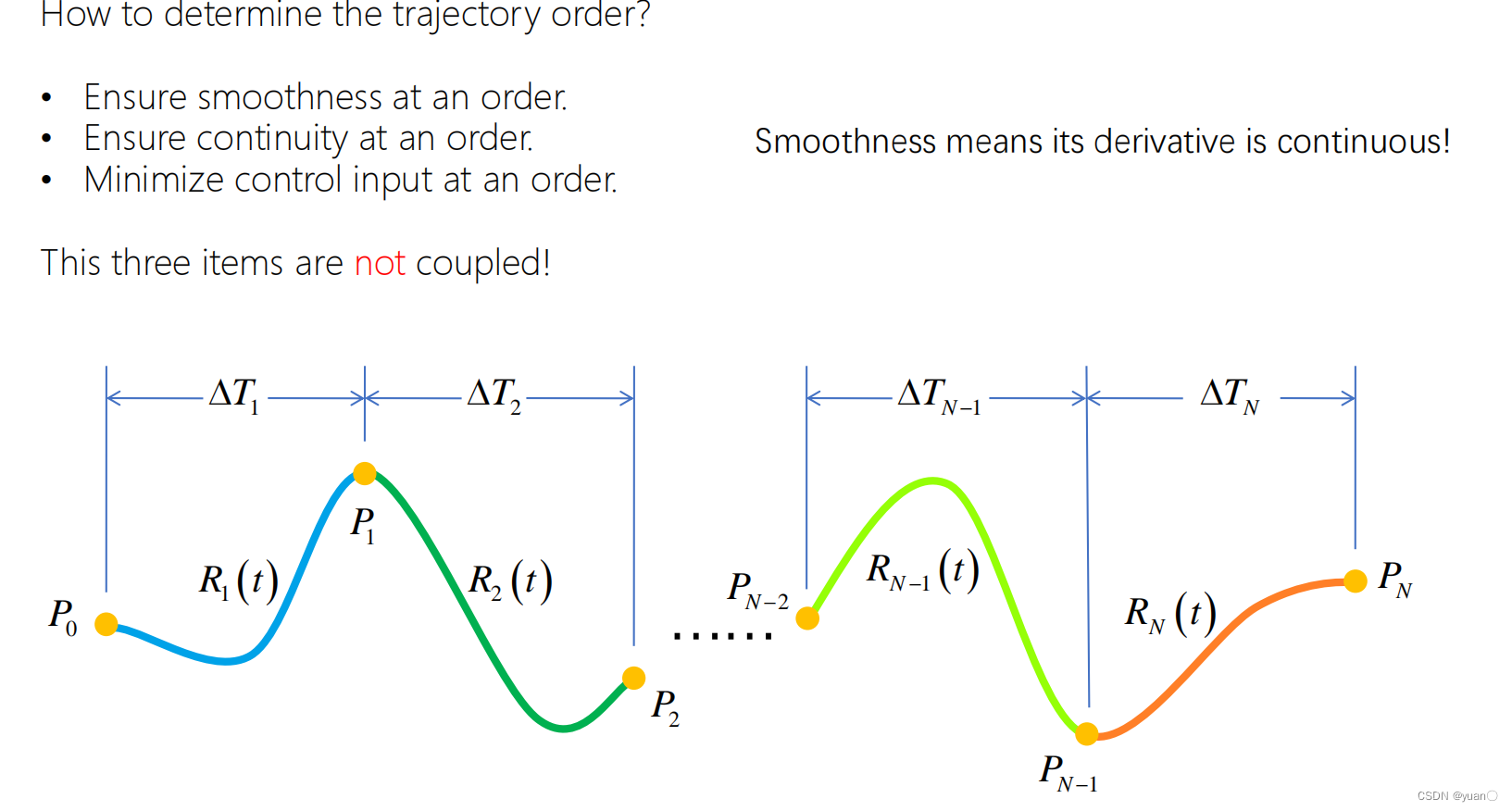
最小化jerk需要五次轨迹(一段轨迹)
最小化snap需要7次轨迹(一段轨迹)
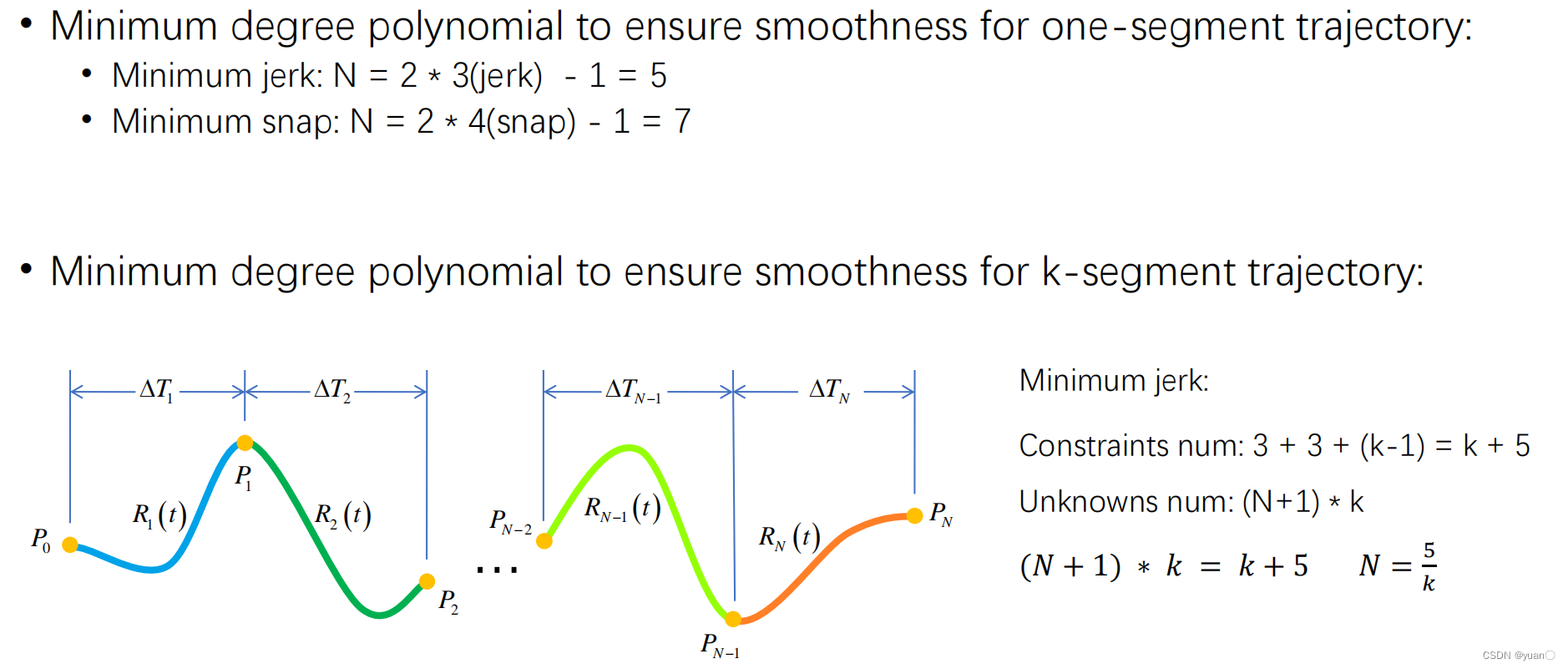
时间线的设置

一段轨迹目标函数

微分约束,对于起点和终点是k = 0, 1, 2, 3,即要求p,v,a,j;对于waypoint则通常要求k = 0,即只要求p,这两种情况都可以写成矩阵形式的等式约束

连续性约束,对于waypoint虽然不要求v,a,j,但是要求左右两段的轨迹在waypoint处的各阶导数是相等的

Convex Optimization(凸优化)
凸优化相关课程:
- Boyd斯坦福公开课
- HKUSThttps://github.com/KellyHwong/convex-hkust
- 凸优化入门教材与课程推荐与整理
凸函数和凸集
凸函数的数学定义是:若
f
(
x
)
f(x)
f(x)在区间
I
I
I上连续,
I
I
I是实数集上的一个区间,且对于任意
x
,
y
∈
I
x,y \in I
x,y∈I和任意
λ
∈
[
0
,
1
]
\lambda \in [0,1]
λ∈[0,1],都有
f
(
λ
x
+
(
1
−
λ
)
y
)
≤
λ
f
(
x
)
+
(
1
−
λ
)
f
(
y
)
f(\lambda x + (1-\lambda)y) \leq \lambda f(x) + (1-\lambda)f(y)
f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y)则
f
(
x
)
f(x)
f(x)在区间
I
I
I上为凸函数。其中,
λ
\lambda
λ称为权值或混合比例。该定义是几何意义下的,即对于函数上的任意两点,函数值在这两点间的线段上的每个点都不超过该点对应的线性函数上的值。凸函数也可以用二阶导数的形式定义为
f
′
′
(
x
)
≥
0
f''(x)\geq 0
f′′(x)≥0。
凸集的数学定义:在欧几里得空间中,一个集合
S
S
S为凸集,当且仅当对于任意
x
,
y
∈
S
x,y\in S
x,y∈S和
0
≤
λ
≤
1
0\leq \lambda\leq 1
0≤λ≤1,都有
λ
x
+
(
1
−
λ
)
y
∈
S
\lambda x+(1-\lambda)y\in S
λx+(1−λ)y∈S其中,
λ
\lambda
λ是一个实数,表示
x
1
x_1
x1和
x
2
x_2
x2之间的比例系数。或者说任意集内的两点所构成的线段均在集内则为凸集。
凸优化问题的标准形式
m
i
n
i
m
i
z
e
f
0
(
x
)
s
u
b
j
e
c
t
t
o
f
i
(
x
)
≤
0
i
=
1
,
…
,
m
A
x
=
b
\begin{aligned}\mathrm{minimize}\quad&f_0(x)\\\mathrm{subject~to}\quad&f_i(x)\leq0\quad i=1,\ldots,m\\&\mathrm{A}x=b\end{aligned}
minimizesubject tof0(x)fi(x)≤0i=1,…,mAx=b
其中目标函数
f
0
f_0
f0和不等式约束函数
f
i
(
x
)
f_i(x)
fi(x)都是凸函数,
A
x
=
b
Ax=b
Ax=b要求是仿射的,
x
x
x的定义域要是一个凸集
Linear Programming (LP):线性规划问题
minimize x c T x + d subject to G x ≤ h A x = b \begin{aligned} \underset{x}{\operatorname*{minimize}}\quad &c^Tx+d \\ \text{subject to}\quad &Gx\leq h \\ &Ax=b \end{aligned} xminimizesubject tocTx+dGx≤hAx=b
Quadratic Programming (QP):二次规划问题
minimize x 1 2 x T P x + q T x + r subject to G x ≤ h A x = b \begin{aligned} \underset{x}{\operatorname*{minimize}}\quad &\frac1 2 x^TPx+q^Tx +r \\ \text{subject to}\quad &Gx\leq h \\ &Ax=b \end{aligned} xminimizesubject to21xTPx+qTx+rGx≤hAx=b
Quadratically Constrained QP (QCQP):具有二次约束的二次规划问题
QCQP(Quadratically Constrained Quadratic Program)可以用如下形式表示:
$ minimize x ( 1 / 2 ) x T P 0 x + q 0 T x + r 0 s u b j e c t t o ( 1 / 2 ) x T P i x + q i T x + r i ≤ 0 i = 1 , … , m A x = b \begin{aligned}\underset{x}{\operatorname*{minimize}}\quad&(1/2)x^TP_0x+q_0^Tx+r_0\\\mathrm{subject~to}\quad&(1/2)x^TP_ix+q_i^Tx+r_i\leq0\quad i=1,\ldots,m\\&Ax=b\end{aligned} xminimizesubject to(1/2)xTP0x+q0Tx+r0(1/2)xTPix+qiTx+ri≤0i=1,…,mAx=b约束函数也是凸函数
其中, x ∈ R n x \in \mathbb{R}^n x∈Rn 是优化变量, P 0 ∈ S n P_0 \in \mathbb{S}^n P0∈Sn, P i ∈ S n P_i \in \mathbb{S}^n Pi∈Sn, q 0 , q i ∈ R n q_0,q_i \in \mathbb{R}^n q0,qi∈Rn, b i ∈ R b_i \in \mathbb{R} bi∈R, A ∈ R p × n A \in \mathbb{R}^{p \times n} A∈Rp×n, b ∈ R p b \in \mathbb{R}^p b∈Rp, l , u ∈ R n l,u \in \mathbb{R}^n l,u∈Rn,且满足 l i ≤ u i l_i \leq u_i li≤ui。
其中, S n \mathbb{S}^n Sn 表示所有 n × n n \times n n×n 的实对称矩阵的集合。 1 2 x T P i x + q i T x ≤ b i \frac{1}{2} x^T P_i x + q_i^T x \leq b_i 21xTPix+qiTx≤bi 表示关于 x x x 的二次不等式约束, A x = b Ax=b Ax=b 表示线性等式约束, l i ≤ x i ≤ u i l_i \leq x_i \leq u_i li≤xi≤ui 表示变量的下界和上界约束。目标是最小化目标函数 1 2 x T P 0 x + q 0 T x \frac{1}{2} x^T P_0 x + q_0^T x 21xTP0x+q0Tx。
Second-Order Cone Programming (SOCP):二阶最优化问题
SOCP是二次锥规划(Second Order Cone Programming)的缩写。二次锥规划是指优化问题的约束条件由二次锥组成的一类凸优化问题。
二次锥规划的一般形式为:
minimize c T x subject to ∣ ∣ A i x + b i ∣ ∣ 2 ≤ c i T x + d i , i = 1 , . . . , m F x = g \begin{aligned} \text{minimize} \quad & c^Tx \\ \text{subject to} \quad & ||A_ix + b_i||_2 \leq c_i^Tx + d_i, \quad i=1,...,m \\ & Fx = g \end{aligned} minimizesubject tocTx∣∣Aix+bi∣∣2≤ciTx+di,i=1,...,mFx=g
其中, x x x是优化变量, c c c是一个向量, A i A_i Ai是矩阵, b i b_i bi是向量, d i d_i di和 g g g是标量。
主要约束条件是二次锥约束,其中 ∣ ∣ A i x + b i ∣ ∣ 2 ≤ c i T x + d i ||A_ix+b_i||_2 \leq c_i^Tx+d_i ∣∣Aix+bi∣∣2≤ciTx+di 表示向量 A i x + b i A_ix+b_i Aix+bi与向量 c i T x + d i c_i^Tx+d_i ciTx+di在欧几里得空间中的内积小于等于0。这个约束条件可以写成转化后的形式,即
t ≥ ∣ ∣ A i x + b i ∣ ∣ 2 c i T x + d i − t ≤ 0 \begin{aligned} t \geq ||A_i x + b_i||_2 \\ c_i^T x + d_i - t \leq 0 \end{aligned} t≥∣∣Aix+bi∣∣2ciTx+di−t≤0
其中 t t t是辅助变量,用于确保内积小于等于0。
SOCP可以被视为直接扩展的LP问题。因此,可以使用凸优化进行求解,例如内点法和分支定界法。相较于二次规划,SOCP问题具有更好的凸性。
Semidefinite Programming(SDP)
SDP(Semidefinite Programming)可以用如下形式表示:
min X c T x s . t . F 0 + ∑ i = 1 n X i F i ⪰ 0 X i ⪰ 0 , i = 1 , 2 , … , n \begin{aligned} \min_{X} \ & c^T x\\ s.t. \ & F_0 + \sum_{i=1}^n X_i F_i \succeq 0 \\ & X_i \succeq 0, i = 1, 2, \ldots, n \end{aligned} Xmin s.t. cTxF0+i=1∑nXiFi⪰0Xi⪰0,i=1,2,…,n
其中, X i ∈ S n i X_i \in \mathbb{S}^{n_i} Xi∈Sni 是对称半正定矩阵, c ∈ R n c \in \mathbb{R}^n c∈Rn 是常数向量, F i ∈ S n i F_i \in \mathbb{S}^{n_i} Fi∈Sni 是常数对称矩阵, F 0 ∈ S n 0 F_0 \in \mathbb{S}^{n_0} F0∈Sn0 是常数对称矩阵, ⪰ 0 \succeq 0 ⪰0 表示半正定矩阵。目标是最小化目标函数 c T x c^T x cTx,满足矩阵不等式约束 F 0 + ∑ i = 1 n X i F i ⪰ 0 F_0 + \sum_{i=1}^n X_i F_i \succeq 0 F0+∑i=1nXiFi⪰0 和半正定约束 X i ⪰ 0 , i = 1 , 2 , … , n X_i \succeq 0, i = 1, 2, \ldots, n Xi⪰0,i=1,2,…,n。
不难看出,SDP 可以看做是约束条件为对称半正定矩阵的凸优化问题。其中矩阵不等式约束保证了问题是凸的。
Closed-form Solution to Minimum Snap
论文:Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments, Charles Richter, Adam Bry, and Nicholas Roy
利用QP求解器求解的是Minimum Snap问题的数值解,另一种解法,从代数上直接求出Minimum Snap问题的解析解,即Minimum Snap问题的闭式解法。
Decision variable mapping变量映射
之前的优化问题如下:
J
=
[
p
1
⋮
p
M
]
T
[
Q
1
0
0
0
⋱
0
0
0
Q
M
]
[
p
1
⋮
p
M
]
J=\begin{bmatrix}\mathbf{p}_1\\\varvdots\\\mathbf{p}_M\end{bmatrix}^T\quad\begin{bmatrix}\mathbf{Q}_1&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\ddots&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{Q}_M\end{bmatrix}\begin{bmatrix}\mathbf{p}_1\\\varvdots\\\mathbf{p}_M\end{bmatrix}
J=
p1⋮pM
T
Q1000⋱000QM
p1⋮pM
可以看到,优化的变量是轨迹多项式的系数
p
0
,
p
1
,
.
.
.
,
p
M
p_0,p_1,...,p_M
p0,p1,...,pM,系数没有实际的物理含义,例如
p
10
t
10
p_{10}t^{10}
p10t10时,当
t
t
t较大时,
p
10
p_{10}
p10就可能非常小,会带来轨迹规划问题上数值不稳定的问题。因此,我们需要将轨迹优化上系数的问题转化为轨迹点的导数约束(也就是各个点的
p
,
v
,
a
p,v,a
p,v,a,拥有物理含义)。通过映射矩阵
M
j
M_j
Mj将待求解的变量
p
j
p_j
pj映射到轨迹点的导数约束
d
j
d_j
dj,即
M
j
p
j
=
d
j
M_jp_j=d_j
Mjpj=dj。
新的目标函数:
J = [ d 1 ⋮ d M ] T [ M 1 0 0 0 ⋮ 0 0 0 M M ] − T [ Q 1 0 0 0 ⋮ 0 0 0 Q M ] [ M 1 0 0 0 ⋮ 0 0 0 M M ] − 1 [ d 1 ⋮ d M ] J=\begin{bmatrix}\mathbf{d}_1\\\varvdots\\\mathbf{d}_M\end{bmatrix}^T\begin{bmatrix}M_1&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\vdots&\mathbf{0}\\\mathbf{0}&\mathbf{0}&M_M\end{bmatrix}^{-T}\begin{bmatrix}\mathbf{Q}_1&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\vdots&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\mathbf{Q}_M\end{bmatrix}\begin{bmatrix}M_1&\mathbf{0}&\mathbf{0}\\\mathbf{0}&\vdots&\mathbf{0}\\\mathbf{0}&\mathbf{0}&\boldsymbol{M}_M\end{bmatrix}^{-1}\begin{bmatrix}\mathbf{d}_1\\\vdots\\\mathbf{d}_M\end{bmatrix} J= d1⋮dM T M1000⋮000MM −T Q1000⋮000QM M1000⋮000MM −1 d1⋮dM
轨迹方程如下:
x
(
t
)
=
p
5
t
5
+
p
4
t
4
+
p
3
t
3
+
p
2
t
2
+
p
1
t
+
p
0
x
′
(
t
)
=
5
p
5
t
4
+
4
p
4
t
3
+
3
p
3
t
2
+
2
p
2
t
+
p
1
x
′
′
(
t
)
=
20
p
5
t
3
+
12
p
4
t
2
+
6
p
3
t
+
2
p
2
\begin{aligned} &x(t)=p_5t^5+p_4t^4+p_3t^3+p_2t^2+p_1t+p_0 \\ &x'(t)=5p_5t^4+4p_4t^3+3p_3t^2+2p_2t+p_1 \\ &\begin{aligned}x''(t)=20p_5t^3+12p_4t^2+6p_3t+2p_2\end{aligned} \end{aligned}
x(t)=p5t5+p4t4+p3t3+p2t2+p1t+p0x′(t)=5p5t4+4p4t3+3p3t2+2p2t+p1x′′(t)=20p5t3+12p4t2+6p3t+2p2
映射矩阵:
M
=
[
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
2
0
0
T
5
T
4
T
3
T
2
T
1
5
T
4
4
T
3
3
T
2
2
T
1
0
20
T
3
12
T
2
6
T
2
0
0
]
\boldsymbol{M}=\begin{bmatrix}0&0&0&0&0&1\\0&0&0&0&1&0\\0&0&0&2&0&0\\T^5&T^4&T^3&T^2&T&1\\5T^4&4T^3&3T^2&2T&1&0\\20T^3&12T^2&6T&2&0&0\end{bmatrix}
M=
000T55T420T3000T44T312T2000T33T26T002T22T2010T10100100
更清晰一点表示,
M
M
M矩阵前三行将
t
=
0
t=0
t=0时的值代入,后三行将
t
=
T
t=T
t=T代入
M
p
i
=
[
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
2
0
0
T
5
T
4
T
3
T
2
T
1
5
T
4
4
T
3
3
T
2
2
T
1
0
20
T
3
12
T
2
6
T
2
0
0
]
[
p
5
p
4
p
3
p
2
p
1
p
0
]
\boldsymbol{M}\textcolor{red}{p_i}=\begin{bmatrix}0&0&0&0&0&1\\0&0&0&0&1&0\\0&0&0&2&0&0\\T^5&T^4&T^3&T^2&T&1\\5T^4&4T^3&3T^2&2T&1&0\\20T^3&12T^2&6T&2&0&0\end{bmatrix}\textcolor{red}{\begin{bmatrix}p_5\\p_4\\p_3\\p_2\\p_1\\p_0\end{bmatrix}}
Mpi=
000T55T420T3000T44T312T2000T33T26T002T22T2010T10100100
p5p4p3p2p1p0
Fixed and free variable separation固定变量和自由变量分解
轨迹中起始点、终点的状态变量(
p
,
v
,
a
,
j
p,v,a,j
p,v,a,j)是确定的,中间点(waypoints)的位置
(
p
)
(p)
(p)是确定的,因此可以通过选择矩阵
C
C
C去分离自由变量(free)
d
F
\mathbf{d}_F
dF以及固定变量(constrained)
d
P
\mathbf{d}_P
dP。因此,可以得到以下的映射关系:
C
T
[
d
F
d
P
]
=
[
d
1
⋮
d
M
]
\mathbf{C}^T\begin{bmatrix}\mathbf{d}_F\\\mathbf{d}_P\end{bmatrix}=\begin{bmatrix}\mathbf{d}_1\\\varvdots\\\mathbf{d}_M\end{bmatrix}
CT[dFdP]=
d1⋮dM
从而目标函数可以写成:
J
=
[
d
F
d
P
]
T
C
M
−
T
Q
M
−
1
C
T
[
d
F
d
P
]
⏟
R
=
[
d
F
d
P
]
T
[
R
F
F
R
F
P
R
P
F
R
P
P
]
[
d
F
d
P
]
J=\begin{bmatrix}\mathbf{d}_F\\\mathbf{d}_P\end{bmatrix}^T\underbrace{\mathbf{C}M^{-T}\mathbf{Q}M^{-1}\mathbf{C}^T\begin{bmatrix}\mathbf{d}_F\\\mathbf{d}_P\end{bmatrix}}_{\mathbf{R}}=\begin{bmatrix}\mathbf{d}_F\\\mathbf{d}_P\end{bmatrix}^T\begin{bmatrix}\mathbf{R}_{FF}&\mathbf{R}_{FP}\\\mathbf{R}_{PF}&\mathbf{R}_{PP}\end{bmatrix}\begin{bmatrix}\mathbf{d}_F\\\mathbf{d}_P\end{bmatrix}
J=[dFdP]TR
CM−TQM−1CT[dFdP]=[dFdP]T[RFFRPFRFPRPP][dFdP]因此目标函数变成一个无约束的二次规划问题,可以闭式求解
J
=
d
F
T
R
F
F
d
F
+
d
F
T
R
F
P
d
P
+
d
P
T
R
P
F
d
F
+
d
P
T
R
P
P
d
P
d
P
∗
=
−
R
P
P
−
1
R
F
P
T
d
F
\begin{aligned}J=\mathbf{d}_F^T\mathbf{R}_{FF}\mathbf{d}_F+\mathbf{d}_F^T\mathbf{R}_{FP}\mathbf{d}_P+\mathbf{d}_P^T\mathbf{R}_{PF}\mathbf{d}_F+\mathbf{d}_P^T\mathbf{R}_{PP}\mathbf{d}_P\\ \mathbf{d}_P^*=-\mathbf{R}_{PP}^{-1}\mathbf{R}_{FP}^T\mathbf{d}_F\end{aligned}
J=dFTRFFdF+dFTRFPdP+dPTRPFdF+dPTRPPdPdP∗=−RPP−1RFPTdF
PS:为什么连续性约束也没有了?因为可以通过设计选择矩阵
C
C
C将中的一个变量映射到
d
\mathbf{d}
d的两个变量中去,这样就满足了连续性约束
C
C
C的设计

Hierarchical approach
用RRT*获取waypoints,再minimum snap生成轨迹
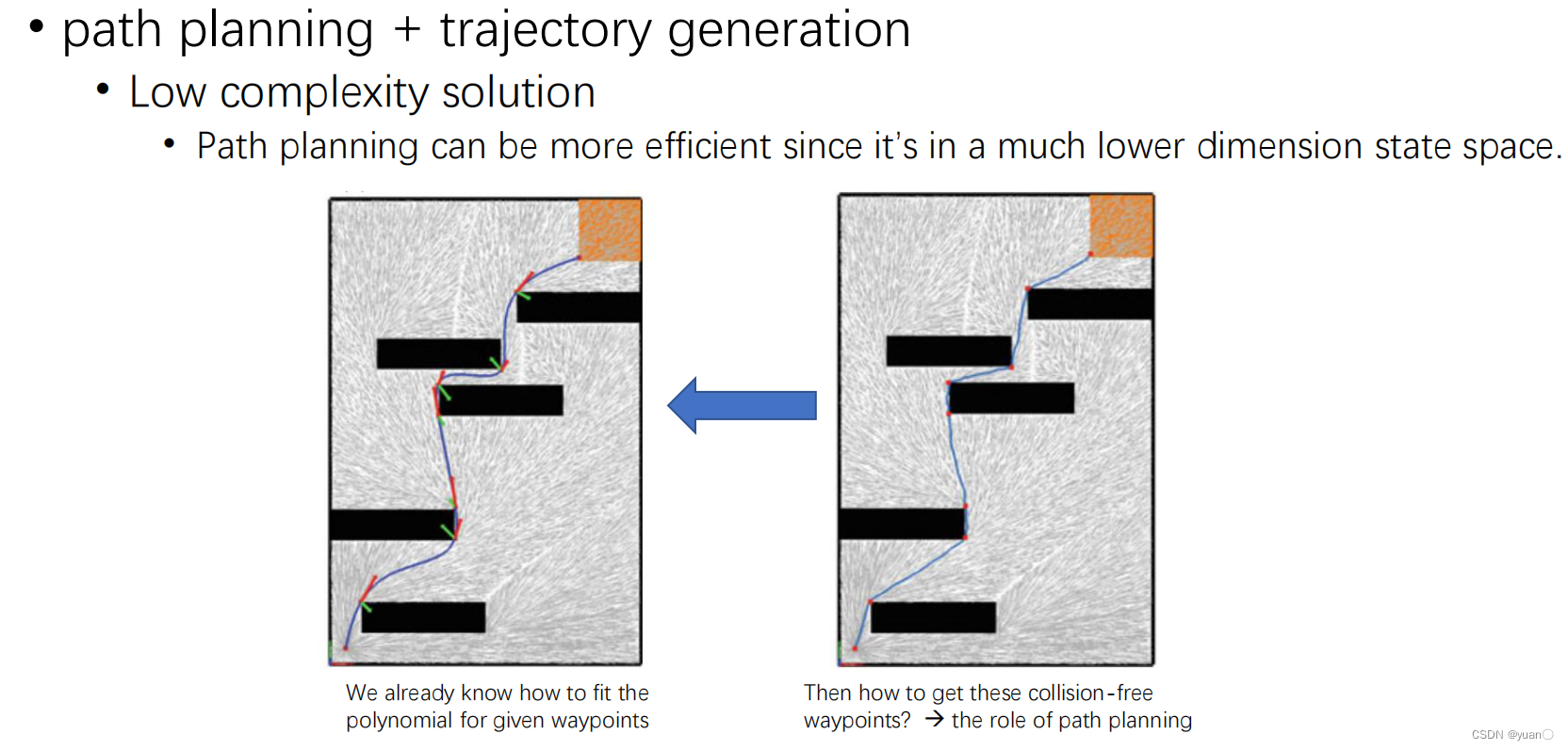
Problem: safety issue
利用RRT寻找的路径是无碰撞的,但是经过轨迹优化后会产生超调

解决方案:在碰撞的部分新增一个路点,重新生成轨迹,如果还是碰撞,就继续从插入路点,极端情况生成的轨迹会无限接近于path planning出的绝对安全的路径
更好的方案?
增加bounding box,硬约束下进行轨迹优化(下一讲细讲)。

Implementation Details(实现细节)
Convex Solvers
| 求解器 | 地址 | 优缺点 |
|---|---|---|
| CVX | http://cvxr.com/cvx/ | 基于MATLAB实现,较慢 |
| Mosek | https://www.mosek.com/ | 非常鲁棒,但只能在x86架构上运行 |
| OOQP | http://pages.cs.wisc.edu/~swright/ooqp/ | 速度快,开源,鲁棒,但代码较老,易读性差 |
| GLPK | https://www.gnu.org/software/glpk/ | 开源,鲁棒,速度快,解LP有优势 |
Numerical Stability

Other engineering stuff

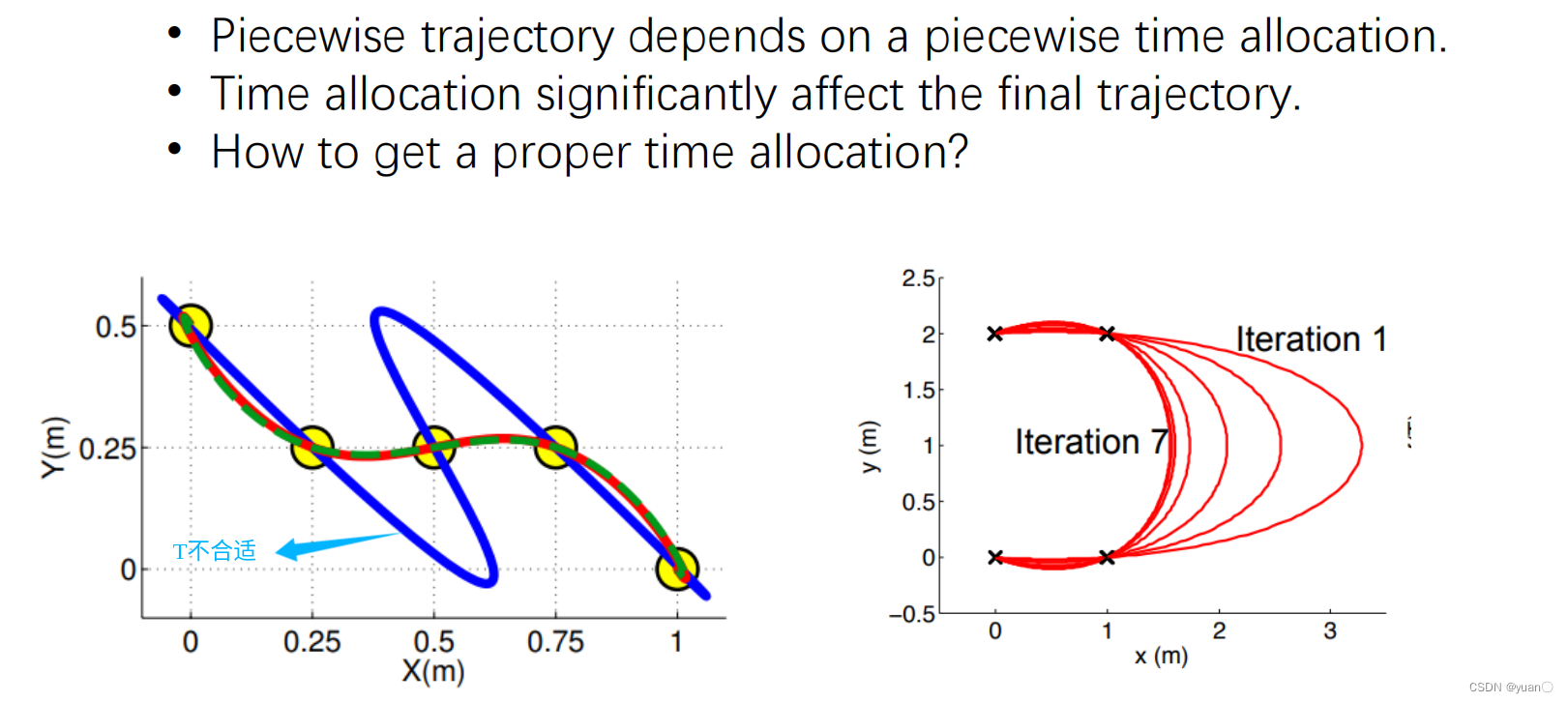
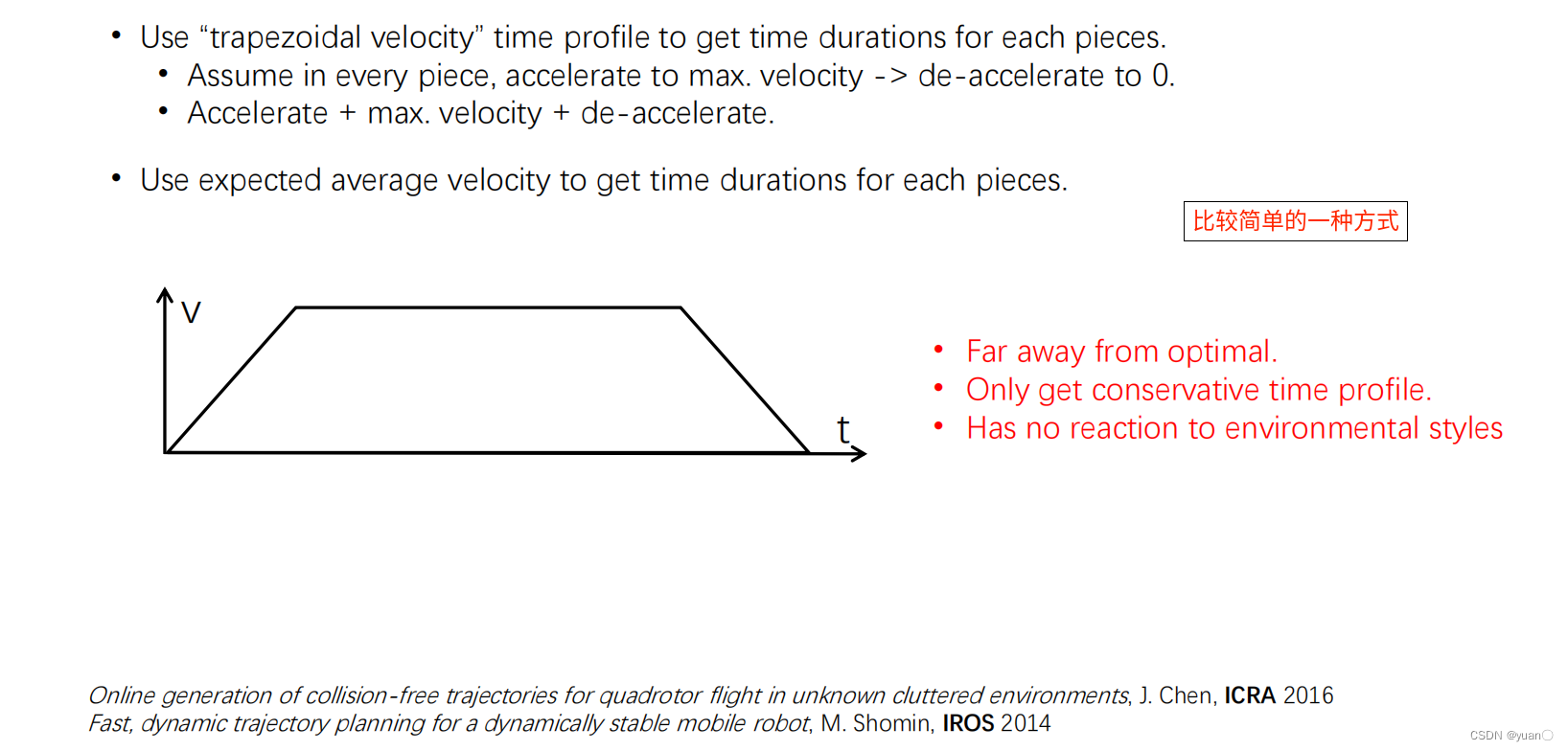
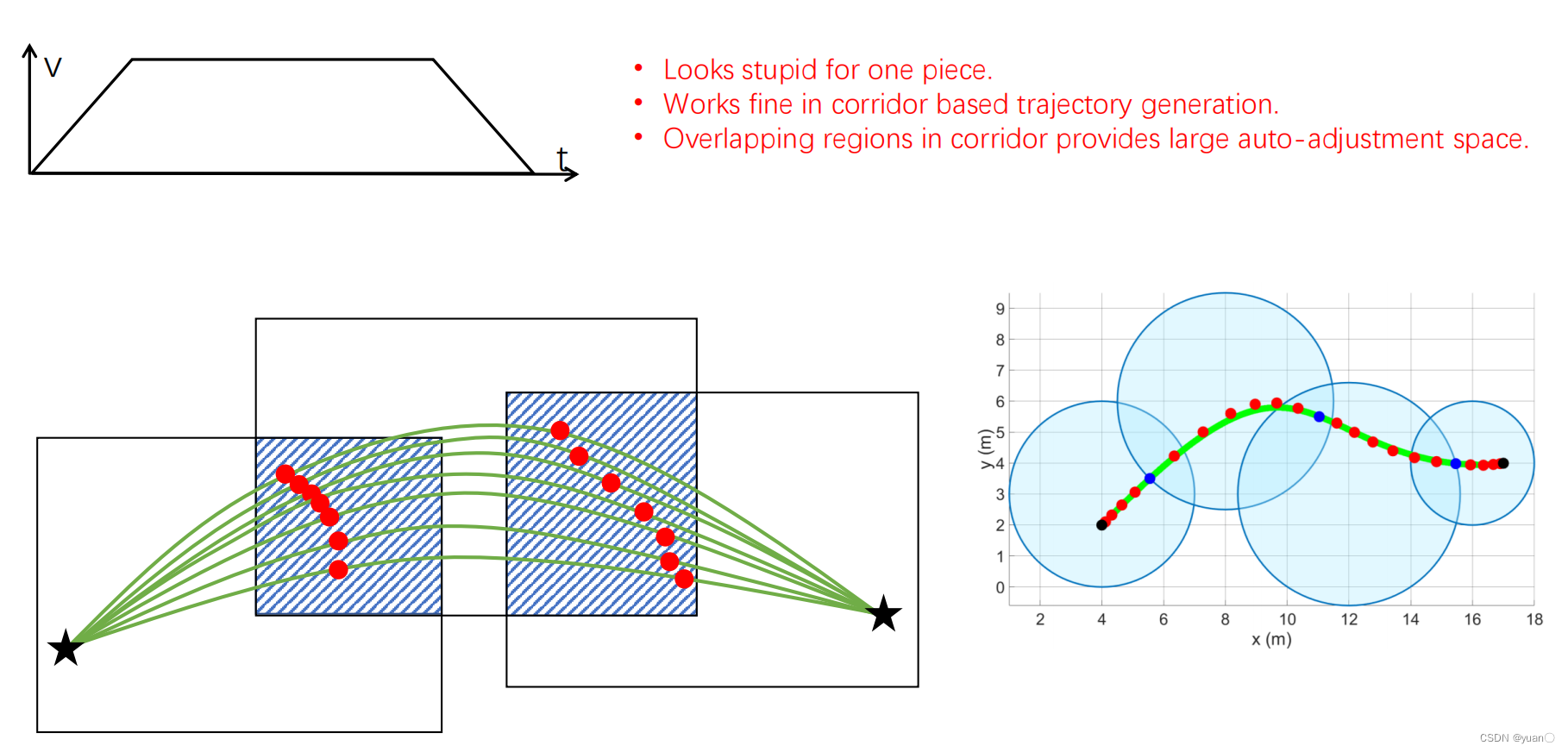
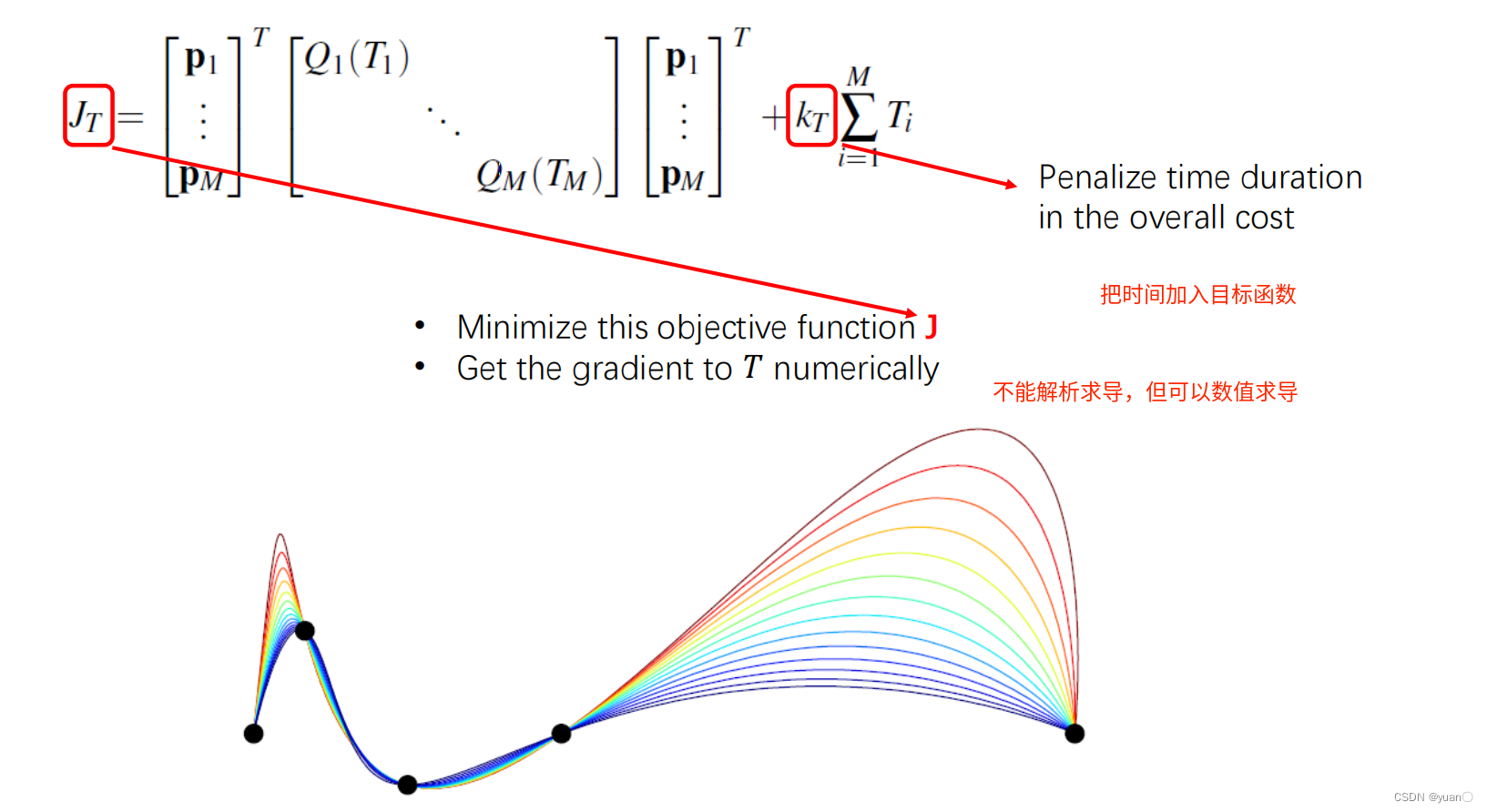
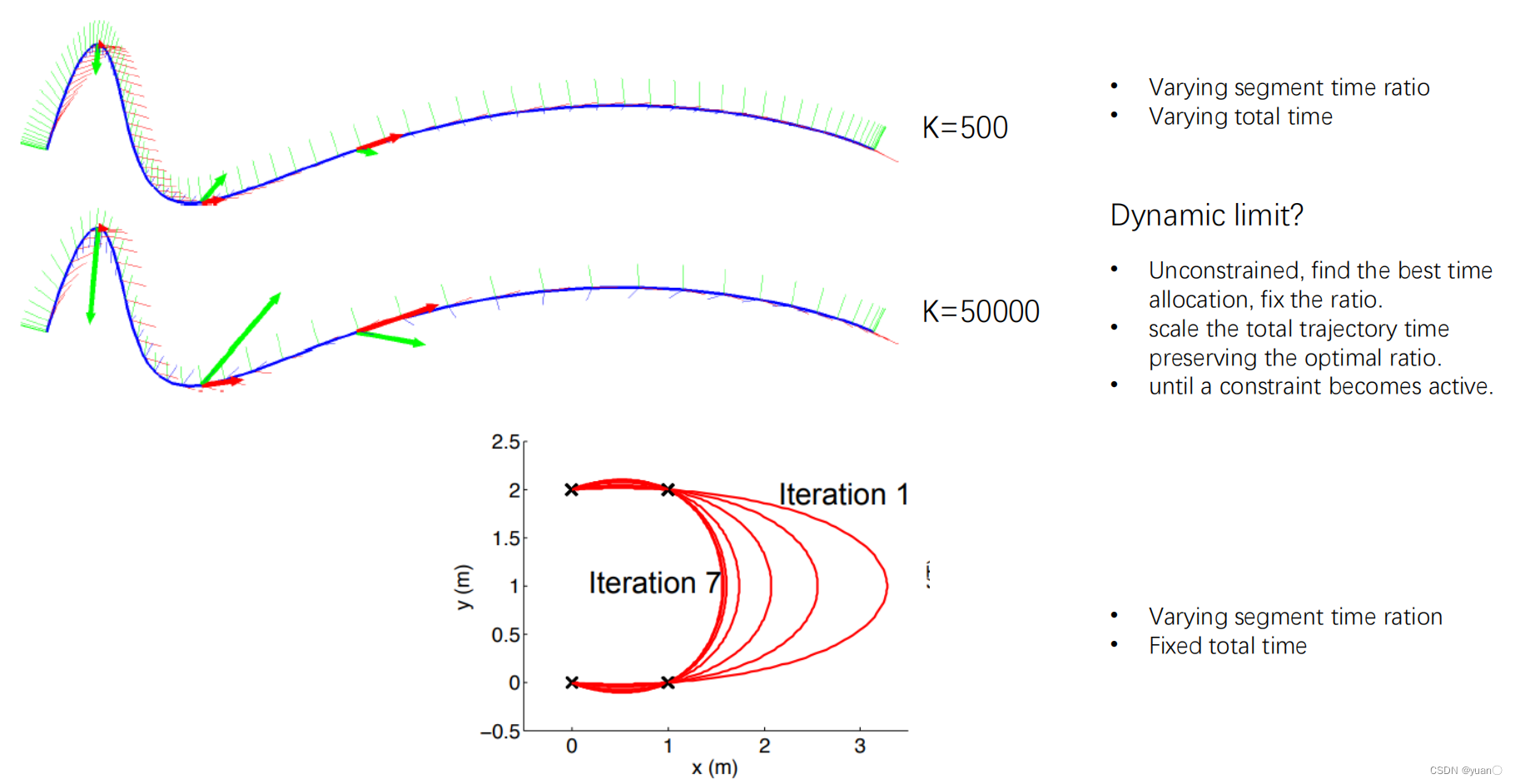
Time Allocation时间分配
参考
[1] Minimum Snap Trajectory Generation and Control for Quadrotors, Daniel Mellinger and Vijay Kumar
[2] Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments, Charles Richter, Adam Bry, and Nicholas Roy