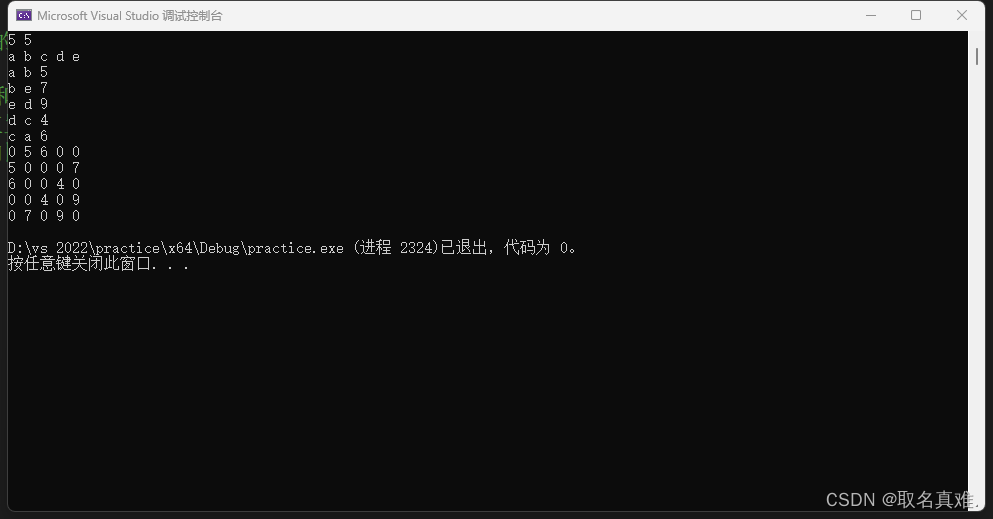
#include<iostream>//无向图邻接矩阵
#define mvnum 100
using namespace std;
typedef char Vertextype;//顶点数据类型
typedef int Arctype;//边权值类型
typedef struct
{
	Vertextype vexs[mvnum];//顶点表
	Arctype arcs[mvnum][mvnum];//邻接矩阵
	int vexnum, arcnum;//当前图的点数和边数
}AMGraph;
int Locatevex(AMGraph G, Vertextype u)//在G图中查找顶点u，存在则返回顶点表中的下标，否则返回-1
{
	for (int i = 0; i < G.vexnum; i++)
		if (u == G.vexs[i]) return i;
	return -1;
}
bool Creategraph(AMGraph& G)
{
	cin >> G.vexnum >> G.arcnum;//输入总顶点数，总边数
	for (int i = 0; i <G.vexnum; i++)
	{
		cin >> G.vexs[i];//依次输入点的信息
	}
	for (int i = 0; i < G.vexnum; i++)//初始化邻接矩阵
		for (int j = 0; j < G.vexnum; j++)
			G.arcs[i][j] = 0;
	for (int k = 0; k < G.arcnum; k++)//构造邻接矩阵
	{
		Vertextype v1, v2;
		int w;
		cin >> v1 >> v2 >> w;//输入一条边的顶点及边的权值
		int i = Locatevex(G, v1);
		int j = Locatevex(G, v2);//确定v1和v2在G中的位置
		G.arcs[i][j] = w;//边<v1,v2>的权值置为w
		G.arcs[j][i] = G.arcs[i][j];//无向图是对称图
	}
	return 1;
}
void Print(AMGraph G)
{
	for (int i = 0; i < G.vexnum; i++)
	{
		for (int j = 0; j < G.arcnum; j++)
			cout << G.arcs[i][j] <<" ";
		cout << endl;
	}
}
int main()
{
	AMGraph G;
	Creategraph (G);
	Print(G);
}