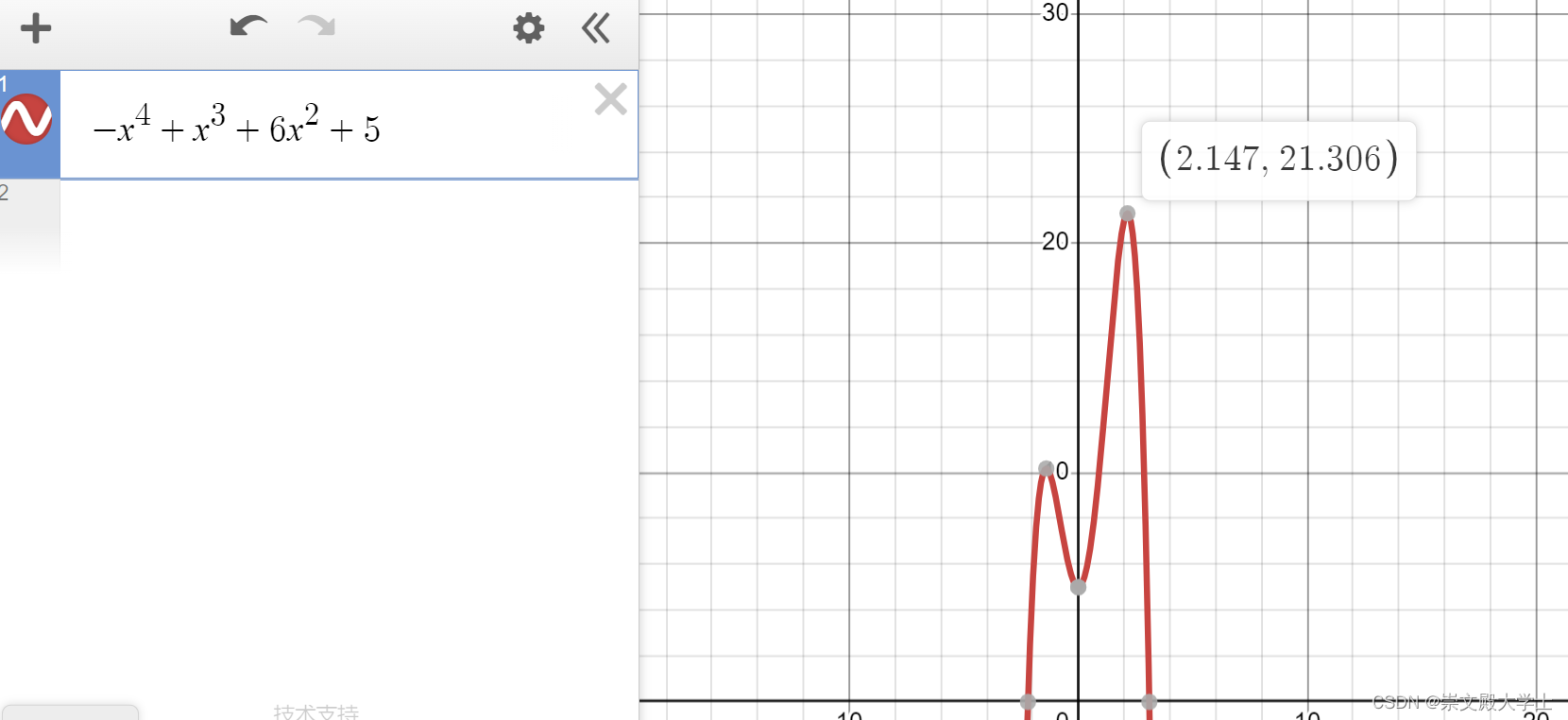
避免落入局部最优解，只要让步长够长即可。
x1 = resultX1 + random1.NextDouble()*100; 如果后面不乘以100，则很大概率落入负数的最大值

            Random random1 = new Random(DateTime.Now.Millisecond);
            double x1 = 0, resultX1=0,max=-999999,maxTemp=0;
            for (int i = 0; i < 54321; i++)
            {
                if (random1.Next(0, 100) % 2 == 0)
                {
                    x1 = resultX1 + random1.NextDouble()*100;//加大后面的100，即可
                }
                else
                {
                    x1 = resultX1 - random1.NextDouble()*100;
                }
                maxTemp = Math.Pow(x1, 4) * (-1) + Math.Pow(x1, 3) + 6 * Math.Pow(x1, 2) + 5;
                if (maxTemp > max)
                {
                    resultX1 = x1;
                    max = maxTemp;
                }
            }
            textBox1.Text = resultX1.ToString();
            textBox2.Text = max.ToString();