本篇文章旨在介绍期权常见希腊字母的计算及应用
本专栏更多侧重于理论及文字方面的展示,文章具体的代码可以参考我的另一个专栏【期权量化】。
【期权量化】专栏有同名文章,并且给出了文章的具体代码。
专栏地址:
http://t.csdn.cn/Y30Hk![]() http://t.csdn.cn/Y30Hk
http://t.csdn.cn/Y30Hk
想了解更多希腊字母的代码,可以参考我的其余文章:
null![]() http://t.csdn.cn/mNIJm
http://t.csdn.cn/mNIJm
null http://t.csdn.cn/4pQZQ
http://t.csdn.cn/4pQZQ
http://t.csdn.cn/bs56Z![]() http://t.csdn.cn/bs56Z
http://t.csdn.cn/bs56Z
http://t.csdn.cn/RaXuO![]() http://t.csdn.cn/RaXuO
http://t.csdn.cn/RaXuO
http://t.csdn.cn/zTFHi![]() http://t.csdn.cn/zTFHi
http://t.csdn.cn/zTFHi
1.前言
期权价格会受到多个因素的影响,如标的资产价格、时间、波动率等,所以引入希腊字母来衡量不同因素对期权价格的影响程度,即Delta、Gamma、Vega、Theta和Rho,从而更综合的研究期权的影响因素。对于单独希腊值的作用,Delta经常被用做计算期权交易杠杆的指标、期权和期货之间对冲时的对冲比率、表示期权到期时成为实值期权的概率等。Gemma值存在方向性风险,对买权者有利,也常用来衡量Delta的稳定性,特别对于Delta中性策略,需要根据Gamma指标及时调整策略。Vega、Theta、Rho通常分别用作衡量波动率风险、时间成本和利率风险的指标。
2.Delat
2.1计算方式
Delta表示期权价格对标的资产价格变化的敏感度,即标的资产价格变动一个单位时,期权价格的变化量。对于看涨/看跌期权,公式可表达为:

同样,基于期权价格与标的资产价格变化的关系,不难看出以下性质:
0≤𝐷𝑒𝑙𝑡𝑎𝑐𝑎𝑙𝑙≤1
−1≤𝐷𝑒𝑙𝑡𝑎𝑝𝑢𝑡≤0
无论是看涨期权还是看跌期权,实值期权的Delta绝对值大于虚值期权Delta绝对值。平值期权Delta绝对值约为0.5。
2.2 Delta的应用
(1)计算杠杆。假设目前黄金期货合约的现货价格为375,有一份3个月后到期的看涨期权,价格为20,Delta=0.8。如果期货合约上涨1%,即3.75,则期权的价格会上涨3.75*0.8=3从涨幅来看,期权合约约上涨15%。则此期权合约的杠杆约为15倍。从实际交易角度来看,当标的资产价格向有利方向变化时,拥有越大绝对值的Delta期权,其价值增长越快;而标的资产价格向不利方向变化时,拥有越小绝对值的Delta期权,其价值下降越小。
(2)对冲指标。由公式可以看出,Delta是期权价格对标的资产价格的偏导数,来测量期权价格对标的资产价格变化的敏感性。因此,Delta可被称作为对冲比率。假设△=0.4,如果买入5手看涨期权,则需要卖出0.4*5=2手对应标的资产的期货合约进行对冲风险;相反的,如果△=-0.4,买入5手看跌期权,则需要买入2手对应标的资产的期货合约对冲风险。
(3)实值概率。一个看涨期权的Delta常常被认为是看涨期权在到期时会是实值的概率。假设行权价为360的黄金看涨期权,△=0.7,那么,12月到期时,此期权的价格有70%的概率会超过360。因此,深度实值期权的Delta绝对值接近1,即深度实值的看涨期权的Delta接近于1.0,而深度实值的看跌期权的Delta接近于-1.0。且期权的虚值程度越深越趋于0。
2.3 Delta倒推行权价
在OTC市场中,期权报价往往采用的是Delta值而不是行权价格,这是一种常见的报价方法。Wystrup在1999年提出了行权价可以表示成Delta的解析解方法,对于看涨期权而言,有:
![]()
对于看跌期权而言,有:
![]()
例子:

也就是说,为了得到0.25的delta值,需要假设行权价为2217.0587。
2.Gamma
2.1 计算方式
Gamma表示Delta随标的资产价格变化而变化的敏感度。即标的资产价格变动一个单位时,Delta的变化量。对于欧式期权而言,看涨期权与看跌期权的gamma数值是一致的:

Gamma的主要特点为:
(1)同一行权价的看涨期权和看跌期权的Gamma值均相等。其中,买入期权的Gamma为正值,卖出期权的Gamma为负值。
(2)平值期权附近的Gamma最大,实值和虚值期权的Gamma值均较小,且趋于0。
2.2 Gamma的应用
(1)衡量Delta稳定性。Gamma经常作为衡量Delta的稳定性。Gamma越高,意味着Delta对标的资产价格的变化越敏感。例如,当运用Delta值估算期权成为实值的概率时,Gamma值可以表示Delta提供的概率的稳定性。
(2)调整Delta中性对冲。Delta经常作为Delta中性的对冲指标,这里的假设是Delta值维持不变,但实际上,由于Gamma的存在,Delta的值是变化的,如果只单一考虑Delta作为对冲因子,则会产生误差。所以当Gamma值很高时,表明Delta的变化速度比较快,Delta中性交易需要及时调整。
(3)衡量方向性风险。Gamma对买入期权者有利,而对于卖出期权者不利。由于买入期权的Gamma为正值,当价格向有利方向运动,头寸会加速增值,当价格向不利方向运动时,头寸会减速减值。然而,对于卖出期权的负值Gamma,情况相反。值得注意的是做多Gamma时,不要忘记时间上的风险。虽然Gamma对买入期权有利,但往往要承担更多期权时间价值的损耗。相反,空头方虽承担一定负Gamma风险,但却得到时间价值上的优势。
3.vega
3.1 计算方式
Vega表示期权价格对标的资产波动率的敏感度,即期权价格变化与隐含波动率变化的比值。看涨期权与看跌期权的vega是一致的。
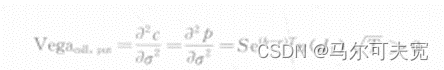
由Vega曲线可得知以下特征:(1)同一行权价的看涨期权和看跌期权的Vega值均相等,且都为正值。(2)平值期权附近的Vega最大,实值和虚值期权的Vega值均较小,随着虚值程度加深,趋于0。
3.2 vega的应用
(1)敏感度。Vega能有效衡量波动率与期权价格之间的变化关系。在期权定价,Black-Scholes模型中,假设条件之一是标的资产的波动率在期权有效期内是固定不变的。但实际上,波动率会受到时间和标的资产等因素的影响而发生变动。
(2)衡量风险。Vega可以表示期权价格面临的波动率风险。Vega值越大,意味着波动率变化引起的期权价格变化越大,面临Vega风险。
4.Theta
4.1 计算方式
Theta表示的是随时间流逝,期权价格损耗的速度。即表示时间每经过一天,期权价值会损耗多少。
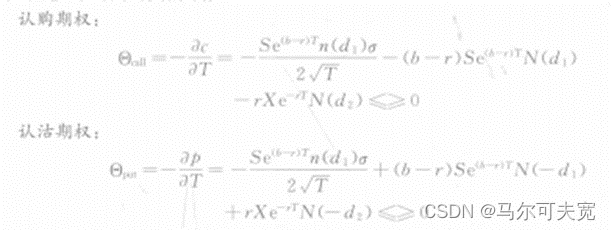
由Vega曲线可得知以下特征:(1)无论是看涨期权还是看跌期权,买方的Theta值通常是负的。这意味着,其他条件不变的情况下,随着到期日的临近,期权的时间价值降低。相应的,期权卖方的Theta通常为正数。值得注意的是,深度实值的看跌期权的Theta值通常为正,因为标的资产价格下跌的是有限的。
(2)通常情况下,平值期权附近的Theta绝对值最大。
4.2 theta的应用
衡量时间价值。Theta值可以粗略计算继续持有期权的时间成本。例如,临近到期日,平值期权的时间价值开始加速衰减,所以对于期权买方,此时买入平值附近的期权成本较大,因为每天时间损耗大,可考虑时间损耗较小的深度实值期权。
5.Rho
5.1 计算方式
Rho是指期权价格对无风险利率变化的敏感程度,即表示无风险利率变化1%,期权价格变化多少。

![]()
由Rho曲线可得知以下特征:(1)看涨期权的Rho为正值,看跌期权的Rho为负值。当标的资产价格较高时,看涨期权对无风险利率比较敏感;当标的资产价格较低时,看跌期权对无风险利率变动会比较敏感。
(2)离到期日越远,Rho的绝对值越大。无风险利率上升,看涨期权的价格上升;而无风险利率上升,看跌期权的价格下降。
5.2 rho的应用
相比于其他希腊值,Rho对期权价格的影响有限,若投资期限较长,也许宏观经济会发生剧烈变化导致利率变化明显,此时需特别注意Rho指标。由于国内的货币政策比较稳健,无风险利率相对比较平稳,对于虚值和深度虚值期权,Rho的影响几乎可以忽略不计。
6.代码部分
见专栏:null![]() http://t.csdn.cn/Y30Hk
http://t.csdn.cn/Y30Hk