1 写在前面的:
其实略微一个大点的机器,一个测试流程需要若干个步骤,都可以用流水线的思维去看待它;
我之前也没往流水线的角度去考虑,那有些机器的时序调度是不好理解的,甚至计算个通量都很麻烦;
下文完全是自己记录的,非常适合我这个行业,不普适
这么重要的思想,我第一次得知,来源竟然是《计算机系统结构_李学干》,一本专升本教材,汗颜...!
2 用一个课本上的例题举例
1.如下图1,横坐标1-9 代表的是时间,纵坐标1-5 代表的是流水线的5个模块;(这个流水线不要狭义的认为是工厂的传送带)
2.模块1 在时间片1和时间片9,举例:可以把他认为是一个机械臂,时间1拿一个原材料来加工,时间9加工完了,丢到成品箱;
3.模块4,你可以理解为是这个模块占用时间较长,一个时间片周期不够,需要两个;
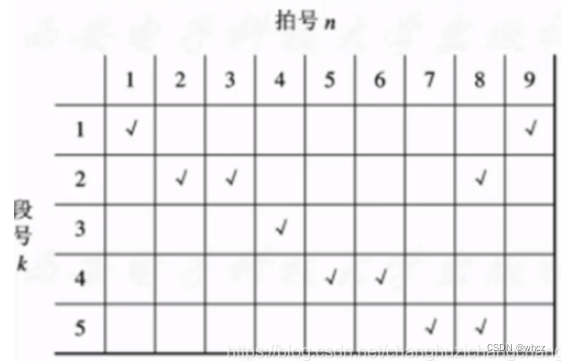
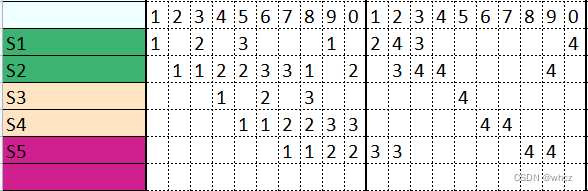
4.如果一个产品需经历模块1-5 ,需占用9个时间片完成;如果批量,一个测试做完,在进行下一个,那么如下图2所示,两个测试需要18个时间片;

5.如果你采用流水线思维,调度逻辑就不会这么干,如下图3所示,每11个时间片,可以完成三个测试;效率(通量)大幅提升
3 调度冲突
从上图看,流水线通量的几个因素:
1.机械设计,要完成一个什么样的产品,按说前期机械非常重要,图1是直接机械决定的;就像一个姑娘,身高、体型、长相;
2.软件设计:至于软件写成图二还是图三或是其他,这个软件因素比较大,类似姑娘的穿衣打扮;
整体看,一个产品能达到什么通量(上限),前期机械直接决定死了
下面说调度冲突
在第一个时间片可以规划第一个测试;
在第二个时间片规划第二个测试,但是s2模块两个测试间冲突,pop
在第三个时间片规划第二个测试,可不冲突的规划
直白的说冲突就是上面的几句话;
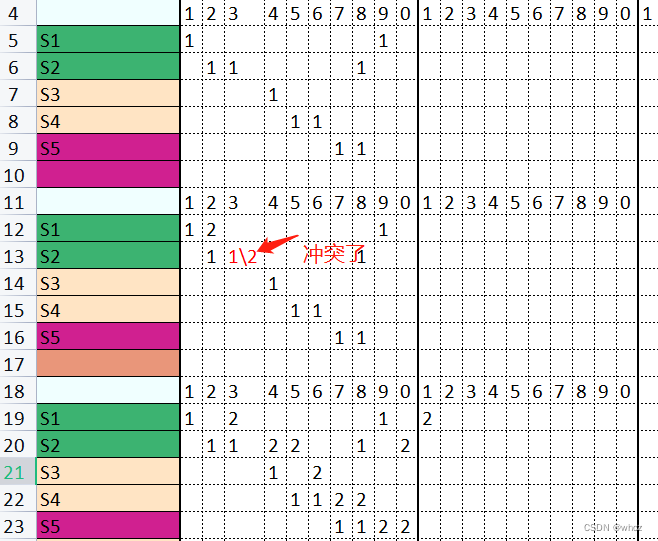
如果计划规划避免冲突
套用下方公式可解:
对于S1,间隔9-1=8拍
对于S2,间隔3-2=1拍、8-2=6拍、8-3=5拍
对于S4,间隔6-5=1拍
对于S5,间隔8-7=1拍
汇集为1,5,6,8,所以延迟禁止表F={1,5,6,8},即第一个和第二个测试间隔1,5,6,8等分钟(拍)执行任务,都会冲突。这是被禁止的。
冲突向量的定义:由延迟禁止表可知,要想不争用流水线的功能段,相邻两个任务送入流水线的间隔拍数就不能为1,3,4,8拍,这些间隔拍数应当禁止使用。可以用一个有N-1位的位向量来表示后续新任务间隔各种不同拍数送入流水线时,是否会发生功能段使用的冲突,称此位向量为冲突向量C (Collison Vector)。
解:根据题意:
N为拍数,N-1=9-1=8位二进制,禁止取1,其余位数为0。即第1,5,6,8位均为1.
冲突向量C =(10110001)
如何画出流水线状态转移图?
首先我们要知道:
初始冲突向量C ,二进制表示,值为1表示禁止相隔的拍数。0,表示可以相隔的拍数。
下一任务相隔x拍进入,可以获该任务进入后的新的冲突向量:
其值= 初始冲突向量 | 当前冲突向量右移x位
套用上述公式计算
注意:计算到什么时候呢?直到不再产生不同的冲突变量为止
第一个任务:
当前冲突向量:初始冲突向量C =(10110001)
表明第二个任务可以间隔的拍数(2,3,4,7)
第二个任务相隔2拍进入
当前冲突向量:10110001>>2=00101100,10110001 | 00101100=10111101
第三个任务可以相隔2拍或者7拍进入
第三个任务相隔2拍进入
当前冲突向量:10111101>>2=00101111,10110001 | 00101111=10111111
第四个任务只能相隔7拍进入
第四个任务相隔7拍进入
当前冲突向量:10111111>>7=00000001,10110001|00000001=10110001
注意,此时的冲突向量已经不是新的,它和第一个任务的冲突向量是相同的,所以就可以止住了。
那么我们开始画图。
首先我们有三个冲突变量,用方框表示,三个初始变量的关系也要在图上表出来。如下图所示,这就是状态转移图。但是这是不完整的,因为第2任务的时候,我们有四种选择,(2,3,4,7),而我们选择了2,假如我们选择了其它选项,就会产生不同的结果了。
让我们穷尽每种选择,那么最终我们画出来的图将会是:
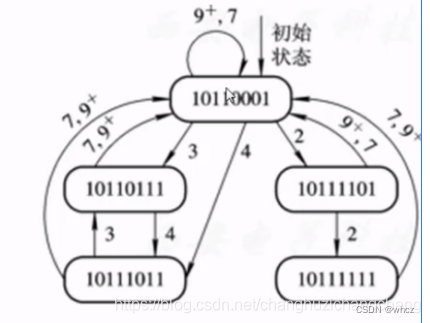
求出最佳调度方案,最小平均延迟及流水线的最大吞吐率
调度方案如何获取,看我们绘制出来的状态转移图,从初始冲突变量开始,到不再出现新的冲突变量结束。
即,调度方案是指构成循环。(3,4)这个调度方案,执行起来就是:3,4,3,4,3,4。。。不停循环,形成一个呈周期性重复的方案。综上可得,调度方案有如下几种:
要想找出一种最佳调度方案使流水线的吞吐率最高,只要计算出每种调度方案的平均间隔拍数,找到其中最小即可。
由上表可知,采用先隔3拍后隔4拍轮流给流水线送入任务的调度方案是最佳的。即平均每隔3.5拍送入一个任务,吞吐率最高。尽管(4,3)调度方案平均间隔也是3.5拍,但若实际流入任务数是循环所需任务的整数倍,则其实际吞吐率会相对低些,所以不作为最佳调度方案。
意思是什么呢?
如当前题目,
(3,4)这个调度方案,构成循环所需任务就是2个。假如实际流入任务数是4个,即整数倍,那么(3,4)调度方案执行起来就是3,4,3;(第一个任务直接进入的,不用间隔)
说明按(3,4)调度方案输入4个任务,全部完成时间为3+4+3+9=19(拍),实际吞吐率Tp=4/19(任务/拍)
(4,3)调度方案执行起来就是4,3,4说明按(4,3)调度方案输入4个任务,全部完成时间为4+3+4+9=20(拍),实际吞吐率Tp=4/20(任务/拍)。显然这个吞吐率比上面的低。
那为什么要强调整数倍,是因为非整数倍情况,假如实际流入任务数是3个,3+4+9=4+3+9,此时它们的实际吞吐率是一样的。
解得:
流水线的最小平均延迟为3.5拍
此时流水线的最大吞吐率Tpmax= 1/3.5(任务/拍)
同为3.5拍的(3,4)和(4,3)调度方案,又因为实际流入任务数是循环所需任务的整数倍时,(3,4)则其实际吞吐率会相对高些(上面已证),所以最佳调度方案:(3,4)
4 结尾
1.这是网上找的一个其他例子,时序排的较为密集,说明前期机械涉及较为合理,利用率较高,跑起来应该是风生水起
2.根据上一节计算公式,绘制了下图
差值为:1、2、3、5、6、7
延迟禁止表F={1、2、3、5、6、7}
执行任务冲突向量的定义:N-1
(92-1-7个0)1110111 第一个任务: 第一个任务初始冲突向量C =((92-1-7个0)1110111)
表明第二个任务可以间隔的拍数(4,8,9,10,11,12,…)第二个任务:右移4位 初始冲突向量C =(1110111) 当前冲突向量:1110111>>4=0000111,
1110111|0000111=1110111 和初始值一致,无需继续
3.在总结下
- 前期机械设计,决定了通量上限;
- 软件设计决定了最终通量,肯定是小于且不等于上限的;
- 电子、软件、机械共同努力,可降低单位时间片的时间,也可提升通量(比如第一个例子,一个测试是要9个时间片,一个时间片如果前期是10s,后期通过缩短短板模块的机械运行举例,更换性能更好的电机或机械臂,把单位时间片提升至8s,那么通量整体可提升25%)