栈和队列经典面试题

news2024/11/28 7:45:57

目录

一、括号匹配问题

20. 有效的括号 - 力扣（LeetCode）

题目

思路

完整代码

二、用队列实现栈

225. 用队列实现栈 - 力扣（LeetCode）

题目

思路

代码实现

构造一个栈

用队列实现栈的接口

第一个接口：创建并初始化栈

第二个接口：入栈

第三个接口：出栈

第四个接口：取栈顶元素

第五个接口：判断栈是否为空

第六个接口：销毁栈

总代码

三、用栈实现队列

232. 用栈实现队列 - 力扣（LeetCode）

题目

 思路

第一个接口：创建并初始化队列

第二个接口：入队

第三个接口：出队

第四个接口：取队头元素

 第五个接口：判断队列是否为空

第六个接口：销毁队列

总代码

四、设计循环队列

622. 设计循环队列 - 力扣（LeetCode）

题目

思路

第一个接口：定义结构体

第二个接口：构造/初始化循环队列

第三个接口：向循环队列插入一个元素

第四个接口：从循环队列中删除一个元素

第五个接口：从队首获取元素

第六个接口：获取队尾元素

第七个接口：检查循环队列是否为空

第八个接口：检查循环队列是否已满

第九个接口：释放空间

总代码

一、括号匹配问题

20. 有效的括号 - 力扣（LeetCode）

题目

给定一个只包括 (，)，{，}，[，] 的字符串，判断字符串是否有效。
有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。

注意空字符串可被认为是有效字符串。

思路

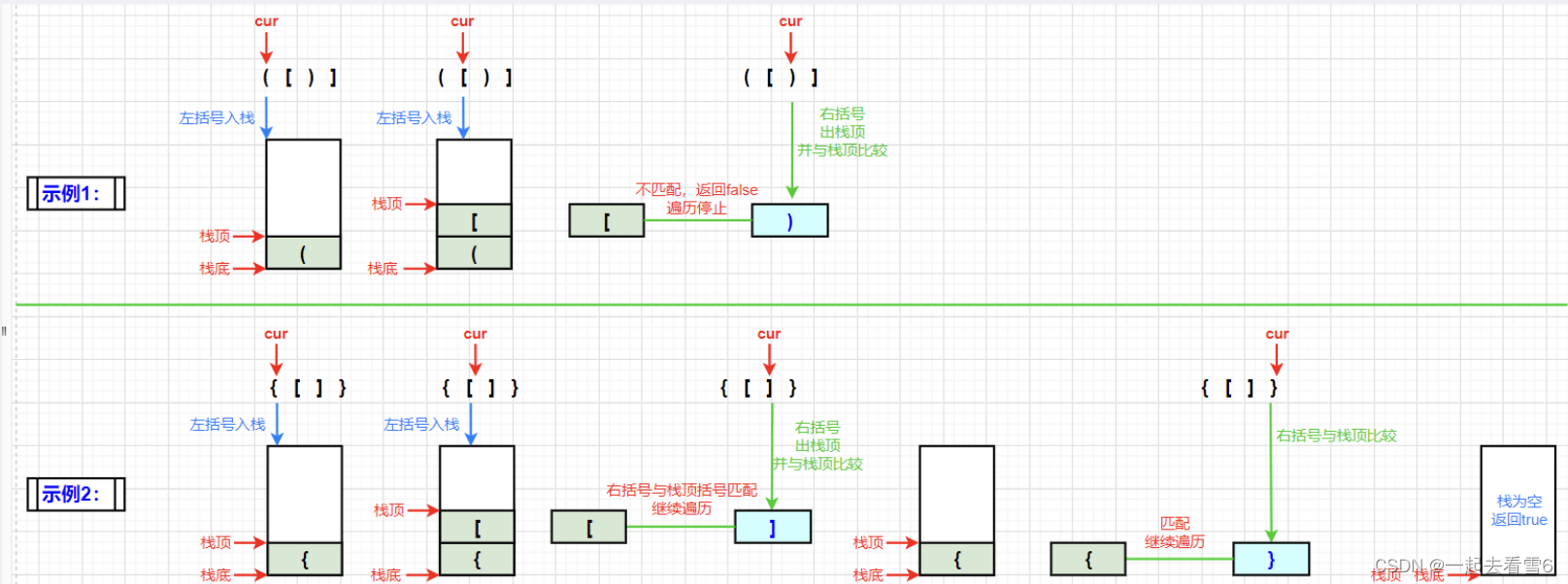
做题前，得先明确解题方案是啥，此题用栈的思想去解决是较为方便的，栈明确指出后进先出。我们可以这样设定：

  1. 遇到左括号“ ( ”、“ [ ”、“ { ”，入栈。
  2. 遇到右括号“ ) ”、“ ] ”、“ } ”，出栈，跟左括号进行匹配，不匹配就报错。

上两句话的意思就是说我去遍历字符串，如果遇到左括号，就入栈；遇到右括号，就出栈顶元素，并判断这个右括号是否与栈顶括号相匹配，若不匹配则返回false，匹配继续遍历字符串，直到遍历完全，遍历后，检查栈是否为空，若为空，则均匹配，返回true，反之false。

S1：遍历输入的括号序列，如果是左括号，进入S2，如果是右括号，进入S3
S2：如果当前遍历到左括号，则入栈
S3：如果当前遍历到右括号，则出栈一个元素，看其是否与当前的右括号组成一对，如果不是，则匹配失败。或者在出栈过程中发生异常(从空栈中出栈)，也匹配失败
S4：若能顺利遍历完成，检查栈中是否还有剩余元素，如果有，则匹配失败；如果没有，则匹配成功。

1、首先将这个字符串转换成字符数组，并初始化一个空栈。

2、遍历到第0个元素，(，为左括号，入栈

3、后面以此类推，遍历完第3个元素[后，栈空间应该是这样的

4、遍历到第4个元素]时，发现为右括号，此时，从栈顶出栈一个左括号，即[，刚好[与]，匹配成一对

5、以此类推，直到第6个元素)，都是匹配的

6、此时，序列已经遍历完毕，但是栈不是空的，所以原序列匹配失败。

 

完整代码

//创建栈结构
typedef char STDataType;
typedef struct Stack
{
	STDataType* a; //存储数据
	int top; //栈顶的位置
	int capacity; //容量
}ST;
//初始化栈
void StackInit(ST* ps);
//销毁栈
void StackDestory(ST* ps);
//压栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//判空
bool StackEmpty(ST* ps);
//访问栈顶数据
STDataType StackTop(ST* ps);
//有效元素个数
int StackSize(ST* ps);
 
//定义：
//初始化栈
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
//销毁栈
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}
//压栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	//如果栈满了，考虑扩容
	if (ps->top == ps->capacity)
	{
		int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2; //检测容量
		ps->a = (STDataType*)realloc(ps->a, newcapacity * sizeof(STDataType));
		if (ps->a == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->capacity = newcapacity; //更新容量
	}
	ps->a[ps->top] = x;//将数据压进去
	ps->top++;//栈顶上移
}
//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	ps->top--;
}
//判空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0; //如果top为0，那么就为真，即返回
}
//访问栈顶数据
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1]; //top-1的位置才为栈顶的元素
}
//有效元素个数
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}
 
//创建好了栈开始实现
bool isValid(char* s) {
    ST st;//先创建一个栈
    StackInit(&st);//初始化栈
    while (*s)
    {
        if (*s == '[' || *s == '(' || *s == '{')
        {
            StackPush(&st, *s); //如果是左括号就入栈
            ++s;
        }
        else
        {
            if (StackEmpty(&st))
            {
                return false; //此处说明前面根本没有左括号，导致栈为空，直接返回false
            }
            char top = StackTop(&st); //获取栈顶元素
            StackPop(&st); //出栈顶元素，接下来进行匹配
            if ((*s == ']' && top != '[')
                || (*s == ')' && top != '(')
                || (*s == '}' && top != '{'))
            {
                StackDestory(&st); //返回前先销毁，防止内存泄漏
                return false; //如果不匹配，直接返回false
            }
            else
            {
                //此时匹配，继续比较，直到遍历结束
                ++s;
            }
        }
    }
    //栈为空，说明所有左括号都匹配
    bool ret = StackEmpty(&st);
    StackDestory(&st); //返回前先销毁，防止内存泄漏
    return ret;
}

二、用队列实现栈

225. 用队列实现栈 - 力扣（LeetCode）

题目

思路

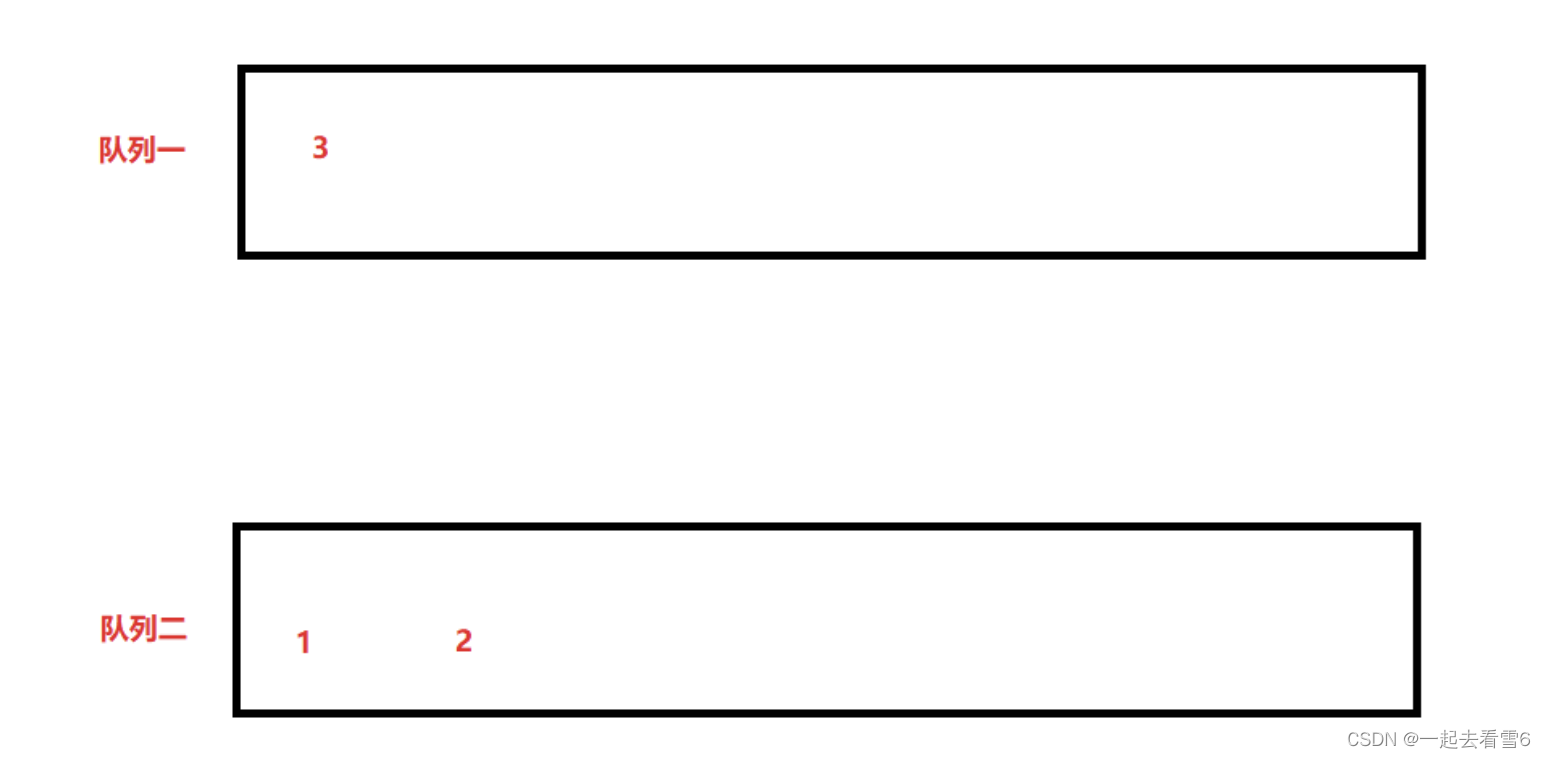
我们这里使用两个队列 

 

入栈数据1、 2、 3

可以将数据入队列至队列一或者队列二。

 

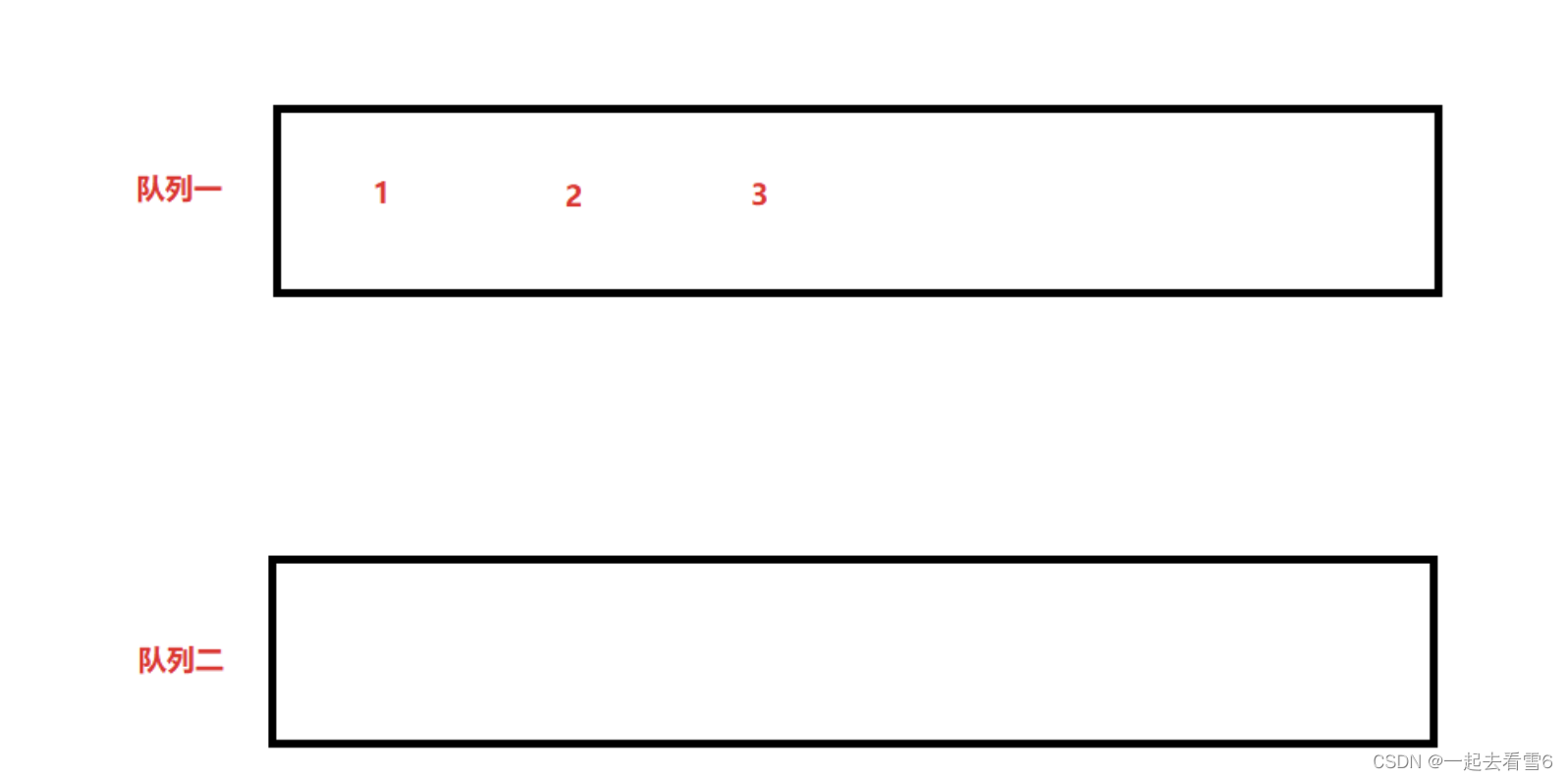
如何出栈？

 但出栈要先出1，怎么办？

第一步：

将队列一出队n-1个至队列二。

 

第二步：

pop队列一的最后一个元素。

 

int myStackPop(MyStack* obj) 
{
    Queue* empty=&obj->q1;
    Queue* nonempty=&obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        nonempty=&obj->q1;
        empty=&obj->q2;
    }
    while(QueueSize(nonempty)>1)
    {
        QueuePush(empty,QueueFront(nonempty));
        QueuePop(nonempty);
    }
    int top=QueueFront(nonempty);
    return top;
}

接下来怎么入栈呢？

将元素入队至不为空的队列。

怎么判断栈空？

队列一和队列二都为空的情况下，栈就是空的。

如何取栈顶元素？

取不为空的队列尾部元素。

总的来说就是，入栈时就将数据插入不为空的队列，出栈就将不为空的队列的前n-1个数据导入至另一个队列，然后pop最后一个元素。

代码实现

构造一个栈

这个栈要包含两个队列

typedef struct 
{
    Queue q1;
    Queue q2;
} MyStack;

在此之前我们要准备好队列的一般接口：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = NULL;
	pq->tail = NULL;
	pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;
	if (pq->tail==NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
		pq->size++;
	}
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;	
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

用队列实现栈的接口

第一个接口：创建并初始化栈
MyStack* myStackCreate() 
{
    MyStack* pst=(MyStack*)malloc(sizeof(MyStack));
    QueueInit(&pst->q1);
    QueueInit(&pst->q2);
    return pst;
}
第二个接口：入栈
void myStackPush(MyStack* obj, int x) 
{
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

入栈简单：只要将数据插入到不为空的队列即可。

入栈之前我们需要判断队列满吗？

不需要，因为我的队列是用单链表实现的，可以无限链接下去。

如果两个队列都为空，该插入到哪个队列呢？

我们可以这样做，如果队列1为空，就插入到队列2，如果不为空，就插入到队列1.

第三个接口：出栈

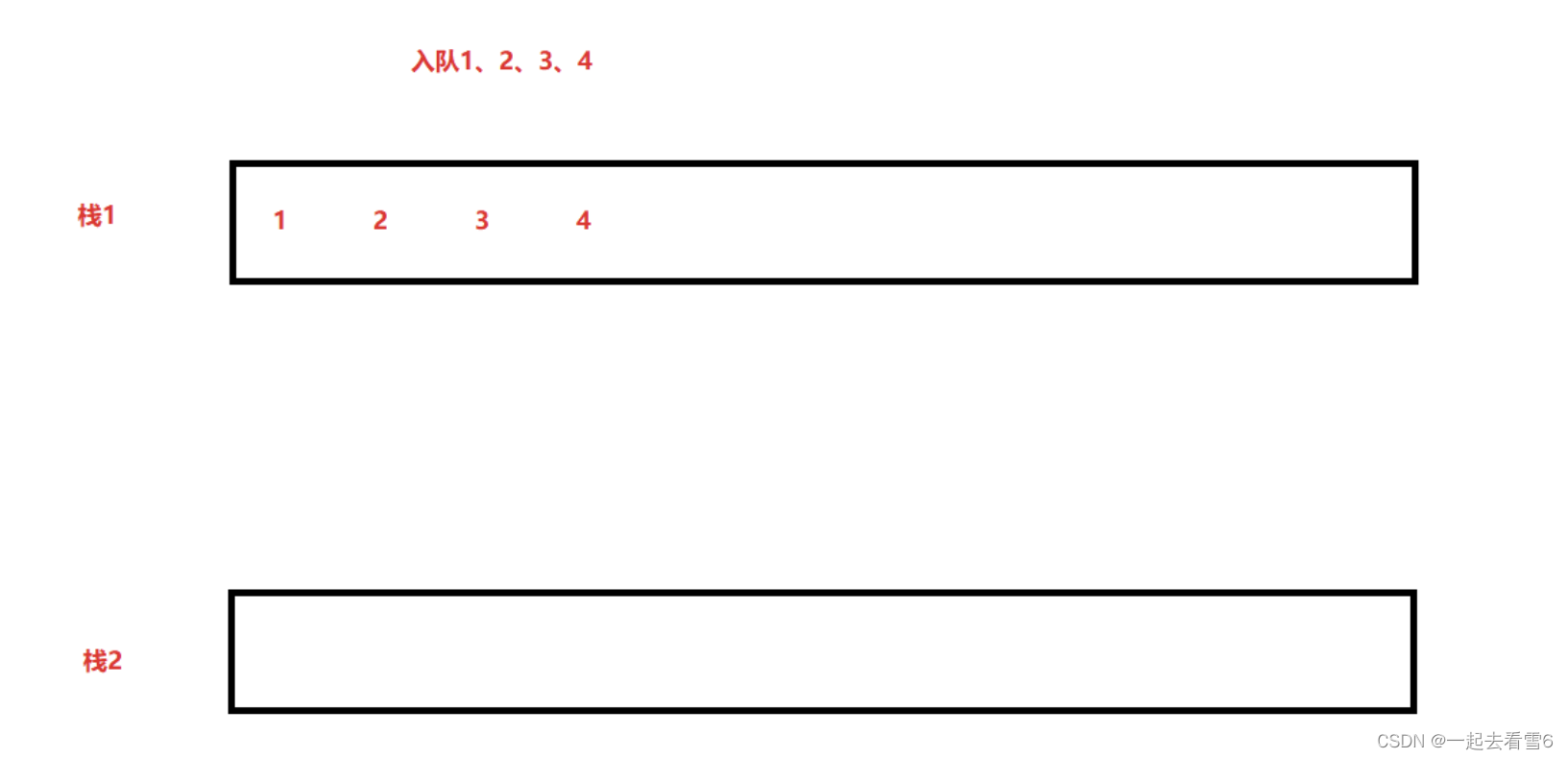
首先我们有两个队列

初始状态它们都是空的

队列一：空

队列二：空

入栈1、2、3、4

执行后

队列一：空

队列二：1、2、3、4

出队列只能先出1，如何出4呢？

把1、2、3先出给队列一

执行后

队列一：1、2、3

队列二：4

然后将4用变量记录并出队，最后返回记录4的变量。

执行后

队列一：1、2、3

队列二：空。

出队三板斧

第一步：即将不为空的队列的前n-1个元素入至为空的队列。

第二步：将剩下的1个元素用变量记录，然后将最后一个元素出队。

第三步：返回用变量记录的元素。

int myStackPop(MyStack* obj) 
{
    Queue* empty=&obj->q1;
    Queue* nonempty=&obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        nonempty=&obj->q1;
        empty=&obj->q2;
    }
    while(QueueSize(nonempty)>1)
    {
        QueuePush(empty,QueueFront(nonempty));
        QueuePop(nonempty);
    }
    int top=QueueFront(nonempty);
    return top;
}
第四个接口：取栈顶元素
int myStackTop(MyStack* obj) 
{
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

取栈顶元素之前我们需要保证栈不为空

这里会用到检查是否为空

如果栈为空，返回false。

取栈顶元素，即取不为空的队列的队尾元素。

第五个接口：判断栈是否为空
bool myStackEmpty(MyStack* obj) 
{
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}

如果两个队列都是空的那么该栈就是空的。

这里多提一下，栈的元素个数怎么求？

栈的元素个数就是那个不为空队列的元素个数。

第六个接口：销毁栈
void myStackFree(MyStack* obj) 
{
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

要将两个队列置空后再去free

用队列实现栈：

我们需要用两个队列实现栈

栈类是于尾插尾删

队列是尾插头删

第一次入栈：两个队列都为空，随便插入一个队列都可

第一次出栈：出栈要出的是尾部数据，队列只能出头部数据，这是队列不能直接实现的。

那么需要将不为空的队列前n-1个数据导入至为空的队列，再将最后一个元素pop掉。

队列一：1、2、3、4

队列二：空

那么导入后

队列一：4

队列二：1、2、3

最后pop最后一个元素

队列一：空

队列二：1、2、3、4

再次尾插：尾插至不为空的队列即可。

总代码

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Queue;

void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDataType x);
void QueuePop(Queue* pq);
QDataType QueueFront(Queue* pq);
QDataType QueueBack(Queue* pq);
bool QueueEmpty(Queue* pq);
int QueueSize(Queue* pq);

void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = NULL;
	pq->tail = NULL;
	pq->size = 0;
}
void QueuePush(Queue* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;
	if (pq->tail==NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
		pq->size++;
	}
}
void QueuePop(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;	
}
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}
bool QueueEmpty(Queue* pq)
{
	assert(pq);
	return pq->head == NULL;
}
int QueueSize(Queue* pq)
{
	assert(pq);
	return pq->size;
}

typedef struct 
{
    Queue q1;
    Queue q2;
} MyStack;


MyStack* myStackCreate() 
{
    MyStack* pst=(MyStack*)malloc(sizeof(MyStack));
    QueueInit(&pst->q1);
    QueueInit(&pst->q2);
    return pst;
}


void myStackPush(MyStack* obj, int x) 
{
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

int myStackPop(MyStack* obj) 
{
    Queue* empty=&obj->q1;
    Queue* nonempty=&obj->q2;
    if(!QueueEmpty(&obj->q1))
    {
        nonempty=&obj->q1;
        empty=&obj->q2;
    }
    while(QueueSize(nonempty)>1)
    {
        QueuePush(empty,QueueFront(nonempty));
        QueuePop(nonempty);
    }
    int top=QueueFront(nonempty);
    return top;
}

int myStackTop(MyStack* obj) 
{
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) 
{
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) 
{
    QueueDestroy(&obj->q1);
    QueueDestroy(&obj->q2);
    free(obj);
}

 

三、用栈实现队列

232. 用栈实现队列 - 力扣（LeetCode）

题目

 思路

第一次入队

将数据1出队操作

将栈1的数据全导入栈2

 

然后栈2进行出栈操作 

此时第一个出栈的就是栈1的头

再次入队5、6、7

直接将5、6、7入栈至栈1

实际我们的对头和队尾是这样的 

 

总而言之：

用两个栈实现一个队列，就得把一个栈专门入队，另一个栈用作出队。这里实现的时候我们用栈1做入队栈，栈2做出队栈。

也就是说，只要将数据入队，直接放入栈1.

出队就直接出栈2的数据，如果栈2为空，这将栈1的数据全部导入栈2.

队列结构体

typedef struct 
{
    ST pushst;
    ST popst;
}MyQueue;

提前准备的栈

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>


typedef char STDataType;


typedef struct Stack
{
	STDataType* a;
	int top;   //栈顶的位置
	int capacity; //容量
}ST;


void STInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}


void STPush(ST* ps, STDataType x)
{
	assert(ps);
	//容量不足，需要进行扩容
	if (ps->top == ps->capacity)
	{
		//增大容量
		int NewCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		//对a指向的数组空间进行增容
		ps->a = (STDataType*)realloc(ps->a, NewCapacity * sizeof(STDataType));
		//检查
		if (ps->a == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->capacity = NewCapacity;


	}
	//增容之后再入栈
	//top是从0位置开始所以是先使用再++
	ps->a[ps->top] = x;
	ps->top++;
}




void STPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	--ps->top;
}


bool STEmpty(ST* ps)
{
	assert(ps);
	if (ps->top > 0)
	{
		return false;
	}
	else
	{
		return true;
	}
	//return ps->top == 0;
}


int STsize(ST* ps)
{
	assert(ps);
	return ps->top;
}


STDataType STTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	//top是从0开始的
	return ps->a[ps->top - 1];
}

第一个接口：创建并初始化队列

MyQueue* myQueueCreate() 
{
    MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->pushst);
    STInit(&obj->popst);
    return obj;
}

第二个接口：入队

void myQueuePush(MyQueue* obj, int x) 
{
    STPush(&obj->pushst,x);
}

我们把栈1做入队栈，栈2做出队栈。

也就是说，只要将数据入队，直接放入栈1.

出队就直接出栈2的数据，如果栈2为空，这将栈1的数据全部导入栈2.

第三个接口：出队

int myQueuePop(MyQueue* obj) 
{
    int front=myQueuePeek(obj);
    STPop(&obj->popst);
    return front;
}

第四个接口：取队头元素
 

int myQueuePeek(MyQueue* obj) 
{
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    return STTop(&obj->popst);
}

 第五个接口：判断队列是否为空

bool myQueueEmpty(MyQueue* obj) 
{
    return STEmpty(&obj->popst)&&STEmpty(&obj->pushst);
}

第六个接口：销毁队列

void myQueueFree(MyQueue* obj) 
{
    STDestroy(&obj->popst);
    STDestroy(&obj->pushst);
    free(obj);
}

用栈实现队列

我们有两个栈要求实现队列的一般接口

栈一：空

栈二：空

第一次入队：入栈至栈一或者栈二都可，这里选择栈一。

假设入队1、2、3、4

栈一：1、2、3、4

栈二:空

出队：要先出1

将栈一全部导入栈二

栈一：空

栈二：4、3、2、1

之后入队就插入至栈一

出队就pop栈二。

总代码

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>


typedef char STDataType;


typedef struct Stack
{
	STDataType* a;
	int top;   //栈顶的位置
	int capacity; //容量
}ST;


void STInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->top = 0;
}


void STPush(ST* ps, STDataType x)
{
	assert(ps);
	//容量不足，需要进行扩容
	if (ps->top == ps->capacity)
	{
		//增大容量
		int NewCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		//对a指向的数组空间进行增容
		ps->a = (STDataType*)realloc(ps->a, NewCapacity * sizeof(STDataType));
		//检查
		if (ps->a == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->capacity = NewCapacity;


	}
	//增容之后再入栈
	//top是从0位置开始所以是先使用再++
	ps->a[ps->top] = x;
	ps->top++;
}




void STPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	--ps->top;
}


bool STEmpty(ST* ps)
{
	assert(ps);
	if (ps->top > 0)
	{
		return false;
	}
	else
	{
		return true;
	}
	//return ps->top == 0;
}


int STsize(ST* ps)
{
	assert(ps);
	return ps->top;
}


STDataType STTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	//top是从0开始的
	return ps->a[ps->top - 1];
}

typedef struct 
{
    ST pushst;
    ST popst;
}MyQueue;


MyQueue* myQueueCreate() 
{
    MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));
    STInit(&obj->pushst);
    STInit(&obj->popst);
    return obj;
}

void myQueuePush(MyQueue* obj, int x) 
{
    STPush(&obj->pushst,x);
}

int myQueuePop(MyQueue* obj) 
{
    int front=myQueuePeek(obj);
    STPop(&obj->popst);
    return front;
}

int myQueuePeek(MyQueue* obj) 
{
    if(STEmpty(&obj->popst))
    {
        while(!STEmpty(&obj->pushst))
        {
            STPush(&obj->popst,STTop(&obj->pushst));
            STPop(&obj->pushst);
        }
    }
    return STTop(&obj->popst);
}

bool myQueueEmpty(MyQueue* obj) 
{
    return STEmpty(&obj->popst)&&STEmpty(&obj->pushst);
}

void myQueueFree(MyQueue* obj) 
{
    STDestroy(&obj->popst);
    STDestroy(&obj->pushst);
    free(obj);
}

四、设计循环队列

622. 设计循环队列 - 力扣（LeetCode）

题目

思路

思路：

1、因为队列是循环的，所以可以用循环链表实现，让链表尾指向链表头即可，但是会有一个问题就是，插入数据的时候，尾插找队列尾的时候不方便，记录队列尾的指针永远指向的都是队列尾的下一个位置（下面会说原因），就需要用循环来找尾

2、可以用数组来实现，数组在内存中是连续的空间，可以直接用两个数组的下标来控制队列的实现，数组实现的弊端就是在循环的时候数组边界需要特殊考虑，但是可以多加个判断条件来判断边界条件即可，相对于用链表实现更优，所以循环队列大多都用数组实现

第一个接口：定义结构体

定义两个数组下标，front指向队列的头，back指向队尾的下一个位置，原因：back最开始只能指向数组的第一个位置，也就是下标为0的位置，插入一个元素之后，back向后移一个位置，如果back指向的就是队尾的最后一个元素，那最开始队列为空的时候back指向哪里呢？所以就矛盾了（用链表实现也是同理）

typedef struct {
    int* a;
    int front;
    int back;
    int k;
 
} MyCircularQueue;

第二个接口：构造/初始化循环队列

首先需要动态开辟一个之前自己定义实现循环队列的结构体，再动态开辟一个数组，这里需要多开辟一个数组空间

多开一个数组空间的原因如下图所示：

多开一个数组空间就是为了判断队列满的时候避免与判断队列空的时候混淆，多开的一个数组空间可以相当于是整个数组中的任何位置，不一定是最后一个位置，随着多次的插入和删除数据，多出来的一个数组空间也会随着改变

MyCircularQueue* myCircularQueueCreate(int k) {
 
    MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    assert(obj);
    obj->a = (int*)malloc(sizeof(int) * (k + 1));
    obj->front = 0;
    obj->back = 0;
    obj->k = k;
 
    return obj;
}

第三个接口：向循环队列插入一个元素

插入一个元素首先要判断队列是否满了（这里判断可以直接调用后面实现的检查队列是否已满的函数直接判断）。队列没有满再进行插入操作：将所要插入的元素放到数组下标为back的位置处，然后back++指向下一个位置，这里就要考虑边界问题了，因为每次插入一个元素之后，back都要向后走一个位置，若back在插入之前就指向的是数组的最后一个位置处（也就是下标为k指向的位置），则插入一个元素之后，back就要指向数组的第一个位置，这样就相当于循环起来了
 

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    assert(obj);
    if(myCircularQueueIsFull(&obj->a))
    {
        return false;
    }
    obj->a[obj->back] = value;
    if(obj->back == obj->k)
    {
        obj->back = 0;
    }
    else
    {
        obj->back++;
    }
    return true;
}

第四个接口：从循环队列中删除一个元素

删除队列的元素首先要判断队列是否为空（这里的判断使用后面实现的检查队列是否为空的函数直接进行判断）。队列不为空再进行删除队列元素操作：因为下标front永远都指向队列的头，删除元素也就是出队列是从队列的头出的，所以在数组实现中直接将下标front++后指向下一个位置，就相当于删除了队列的头元素，这里也就要多一个判断来考虑边界问题，当front指向最后一个位置时也就是下标为k位置时，front向后走一个位置就到了下标为0位置处
 

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    assert(obj);
 
    if(myCircularQueueIsEmpty(&obj->a))
    {
        return false;
    }
    if(obj->front == obj->k)
    {
        obj->front = 0;
    }
    else
    {
        obj->front++;
    }
    return true;
 
}

第五个接口：从队首获取元素

首先也需要判断队列是否为空（使用下面实现的检查队列是否为空的函数进行判断）。不为空：数组下标front永远指向队列的首元素，所以直接返回数组下标为front位置处的元素即可

int myCircularQueueFront(MyCircularQueue* obj) {
    assert(obj);
    if(myCircularQueueIsEmpty(&obj->a))
    {
        return -1;
    }
    return obj->a[obj->front];
}

第六个接口：获取队尾元素

获取队列元素就需要判断队列是否为空（调用下面实现的检查队列是否为空的函数进行判断）。因为back永远指向队列尾的下一个位置处，所以返回队尾元素时，需要返回下标为back-1位置处的元素，边界情况就是back指向数组0位置时，就需要返回它的前一个位置，也就是数组的最后一个位置（下标为k位置）对应的元素

int myCircularQueueRear(MyCircularQueue* obj) {
    assert(obj);
    if(myCircularQueueIsEmpty(&obj->a))
    {
        return -1;
    }
    if(obj->back == 0)
    {
        return obj->a[obj->k];
    }
    return obj->a[obj->back-1];
}

第七个接口：检查循环队列是否为空

front和back相等指向同一个位置时为空

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    assert(obj);
    return obj->front == obj->back;
}

第八个接口：检查循环队列是否已满

back的下一个位置是front时队列为满，特殊情况：同时满足front为0并且back指向数组最后一个位置（也就是k位置处）则队列为满

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    assert(obj);
    if(obj->front == 0 && obj->back == obj->k)
    {
        return true;
    }
    else
    {
        return obj->front == obj->back + 1;
    }
}

第九个接口：释放空间

free动态开辟的实现循环队列的数组，再free动态开辟的循环队列结构体

void myCircularQueueFree(MyCircularQueue* obj) {
    assert(obj);
    free(obj->a);
    free(obj);
}

总代码

typedef struct {
    int* a;
    int front;
    int rear;
    int k;
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->front=0;
    obj->rear=0;
    obj->k=k;

    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front==obj->rear;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return obj->front==(obj->rear+1)%(obj->k+1);
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->a[obj->rear]=value;
    obj->rear++;
    obj->rear%=(obj->k+1);
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    ++obj->front;
    obj->front%=(obj->k+1);
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->rear+obj->k)%(obj->k+1)];
}


void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

/**
 * Your MyCircularQueue struct will be instantiated and called as such:
 * MyCircularQueue* obj = myCircularQueueCreate(k);
 * bool param_1 = myCircularQueueEnQueue(obj, value);
 
 * bool param_2 = myCircularQueueDeQueue(obj);
 
 * int param_3 = myCircularQueueFront(obj);
 
 * int param_4 = myCircularQueueRear(obj);
 
 * bool param_5 = myCircularQueueIsEmpty(obj);
 
 * bool param_6 = myCircularQueueIsFull(obj);
 
 * myCircularQueueFree(obj);
*/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/866742.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

yolo-nas对自定义数据集进行训练,测试详解 香烟数据集 处理损坏的图片数据 对网络摄像头，视频，图片预测

yolo-nas对自定义数据集进行训练,测试详解 香烟数据集 处理损坏的图片数据 对网络摄像头，视频，图片预测

yolov5格式的香烟数据集 https://download.csdn.net/download/qq_42864343/88110620?spm1001.2014.3001.5503 创建yolo-nas的运行环境 进入Pycharm的terminal&#xff0c;输入如下命令 conda create -n yolonas python3.8pip install super-gradients使用自定义数据训练Yo…
阅读更多...
微信小程序隐私协议模板

微信小程序隐私协议模板

在 设置 中找到 用户隐私保护 进行更新&#xff0c;如下图&#xff1a; 具体协议补充可参考如下&#xff1a; 为了分辨用户&#xff0c;开发者将在获取你的明示同意后&#xff0c;收集你的微信昵称、头像 为了显示距离&#xff0c;开发者将在获取你的明示同意后&#xff0c;收…
阅读更多...
E7—使用IBERT IP对QSFP+通信链路眼图测试2023-08-11

E7—使用IBERT IP对QSFP+通信链路眼图测试2023-08-11

1.场景 通常在使用光纤接GT收发器进行通信之前&#xff0c;要测试信号质量以确认硬件链路工作正常&#xff0c;xilinx提供了IBERT&#xff08;Integrated Bit Error Ratio Tester&#xff09;进行高速串行通信接口的测试和调试&#xff0c;以KU系列QSFP光纤收发器4路GTY为例介绍…
阅读更多...
一文详解Git

一文详解Git

一. Git概述 1.1 什么是 Git Git 是一个免费的、开源的分布式版本控制工具&#xff0c; 主要用于管理开发过程中的源代码文件&#xff0c;在软件开发过程中被广泛使用。通过Git仓库来存储和管理这些文件&#xff0c;Git仓库分为二种&#xff1a; 本地仓库&#xff1a;开发人…
阅读更多...
命令执行漏洞

命令执行漏洞

1、命令执行漏洞 1.1、简介 Django是用Python开发的一个免费开源的Web结构&#xff0c;几乎包括了Web使用方方面面&#xff0c;能够用于快速建立高性能、文雅的网站&#xff0c;Diango提供了许多网站后台开发常常用到的模块&#xff0c;使开发者可以专注于业务部分。 1.2、漏…
阅读更多...
【博学谷学习记录】超强总结，用心分享 | 产品经理之AAARR模型和RFM模型

【博学谷学习记录】超强总结，用心分享 | 产品经理之AAARR模型和RFM模型

&#x1f525;前言 本章重点介绍电商行业常用的AARRR模型和RFM模型&#xff0c;并探讨两个模型的实操和适用范围。 &#x1f4c3;目录 &#xff08;一&#xff09;AARRR模型 1.拉新 2.转化 3.留存 4.活跃 5.传播 &#xff08;二&#xff09;RFM模型 1.三个指标的含义 2.RFM模…
阅读更多...
【C++】C++异常

【C++】C++异常

文章目录 1. C语言传统处理错误的方式2. C异常的概念3. 异常的使用3.1 异常的抛出和捕获3.2 异常的重新抛出3.3 异常安全3.4 异常规范 4. C标准库的异常体系5. 自定义的异常体系6. 异常的优缺点 1. C语言传统处理错误的方式 C语言传统的错误处理机制有两个&#xff1a; 终止程…
阅读更多...
IoTDB 小白“踩坑”心得：入门安装部署篇

IoTDB 小白“踩坑”心得：入门安装部署篇

小伙伴介绍&#xff01; 大家好&#xff0c;我是 zai&#xff0c;一个基本功不那么扎实、没有太多经验的大学生。我刚刚加入社区&#xff0c;接触 IoTDB&#xff0c;目前仍处于学习阶段&#xff0c;所以我会跟大家分享我学习过程中踩过的一些雷&#xff0c;以及对应的解决办法&…
阅读更多...
【百度翻译api】中文自动翻译为英文

【百度翻译api】中文自动翻译为英文

欸&#xff0c;最近想做一些nlp的项目&#xff0c;做完了中文的想做做英文的&#xff0c;但是呢&#xff0c;国内爬虫爬取的肯定都是中文 &#xff0c;爬取外网的技术我没有尝试过&#xff0c;没有把握。所以我决定启用翻译&#xff0c;在这期间chatGPT给了我非常多的方法&…
阅读更多...
文件上传以及yml的配置

文件上传以及yml的配置

目录 一、存储本地 二、存储到阿里云 三、配置文件信息 一、存储本地 MultipartFile 常见方法&#xff1a; String getOriginalFilename(); //获取原始文件名 void transferTo(File dest); //将接收的文件转存到磁盘文件中 long getSize(); //获取文件的大小&#xff0c;单…
阅读更多...
Vue2-绑定样式、条件渲染、列表渲染、列表过滤、模糊查询、Vue监测数据原理

Vue2-绑定样式、条件渲染、列表渲染、列表过滤、模糊查询、Vue监测数据原理

&#x1f954;&#xff1a;想只有苦难&#xff0c;做才有答案 更多Vue知识请点击——Vue.js VUE2-Day3 绑定样式1、class绑定2、绑定style样式 条件渲染1、v-show2、v-if条件渲染案例 列表渲染1、v-for2、key的作用与原理&#xff08;重要&#xff09;面试题&#xff1a;react、…
阅读更多...
Android 高手进阶教程(二)之----Android 数据库SQLiteDatabase的使用！！

Android 高手进阶教程(二)之----Android 数据库SQLiteDatabase的使用！！

直接进入主题~ Android 提供了三种数据存储方式&#xff0c;第一种是文件存储;第二种是SharedPreferences 存储;第三种就是数据库SQLiteDatabase 存储。 文件存储我就不用多说了&#xff0c;而SharedPreferences 可以存取简单的数据(int,double,float.etc)&#xff0c;它经常…
阅读更多...
数字孪生有哪些应用场景？

数字孪生有哪些应用场景？

数字孪生技术正在越来越普遍。根据艾瑞咨询2023年调查&#xff0c;2022年中国数字孪生市场规模为104亿&#xff0c;同比增长35.0%。随着各行业数字化转型的推进&#xff0c;国内未来数字孪生市场规模将继续增长&#xff0c;预计2023年国内市场规模将达到375亿元。 数字孪生是指…
阅读更多...
图片预览插件vue-photo-preview的使用

图片预览插件vue-photo-preview的使用

移动端项目中需要图片预览的功能&#xff0c;但本身使用mintui&#xff0c;vantui中虽然也有&#xff0c;但是为了一个组件安装这个有点儿多余&#xff0c;就选用了vue-photo-preview插件实现&#xff08;其实偷懒也不想自己写&#xff09;。 1、安装 npm i vue-photo-preview…
阅读更多...
学以致用：python面向对象和PyEcharts的完美混合技

学以致用：python面向对象和PyEcharts的完美混合技

文章目录 学习目标数据案例分析数据内容需求分析参考代码data_define.pyfile_define.pymain.py 学习目标 使用面向对象思想完成数据读取和处理基于面向对象思想重新认知第三方库使用(PyEcharts) 数据案例分析 数据内容 1月份数据是普通文本&#xff0c;使用逗号分割数据记录&…
阅读更多...
生态系统服务（InVEST模型）

生态系统服务（InVEST模型）

第一天&#xff1a; 1. 生态系统服务理论联系实践案例讲解 2. InVEST模型的开发历程、不同版本的差异及对数据需求的讲解 3. InVEST所需数据的要求&#xff08;分辨率、格式、投影系统等&#xff09;、获取及标准化预处理讲解 4. InVEST运行常见问题及处理解决方法讲解 5.…
阅读更多...
基于 CentOS 7 构建 LVS-DR 群集 配置nginx负载均衡

基于 CentOS 7 构建 LVS-DR 群集 配置nginx负载均衡

环境配置&#xff1a; RHCE客户机192.168.100.146node1lvs192.168.100.145node2RS192.168.100.147node3RS192.168.100.148 配置ipvsadm httpd&#xff1a; [rootnode1 ~]# yum install ipvsadm.x86_64 [rootnode2 ~]# yum install http -y [rootnode2 ~]# systemctl …
阅读更多...
Ubuntu18.04版本安装ROS及出现错误的处理方法

Ubuntu18.04版本安装ROS及出现错误的处理方法

前面的文章是在已安装的ROS基础上做的一些应用&#xff0c;这里我们从零开始安装ROS机器人操作系统。 机器人操作系统(Robot Operating System,ROS)是一个开发机器人软件的框架&#xff0c;里面包含了一系列的工具&#xff0c;库和惯例&#xff0c;目的在于简化在大量不同种类机…
阅读更多...
从一道面试题来学习前台进程和后台进程、孤儿进程和僵尸进程

从一道面试题来学习前台进程和后台进程、孤儿进程和僵尸进程

1、面试题介绍 以前面试&#xff0c;面试官问了一个问题&#xff0c;大意是&#xff1a; 我们在终端中&#xff0c;通过执行 python main.py 命令&#xff0c;会启动一台前台进程直到程序结束。现在我还是想通过执行 python main.py &#xff0c;启动一个后台进程&#xff0c;…
阅读更多...
k8s的yaml文件管理

k8s的yaml文件管理

声明式管理方法&#xff1a; 1.适合于对资源的修改操作2.声明式资源管理方法依赖于资源配置清单文件对资源进行管理资源配置清单文件有两种格式&#xff1a;yaml&#xff08;人性化&#xff0c;易读&#xff09;&#xff0c;json&#xff08;易于api接口解析&#xff09;3.对资…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023