一、问题的提出
螺旋矩阵是一种常见的矩阵形式,它的特点是按照螺旋的方式排列元素。n阶螺旋矩阵是指矩阵的大小为n×n,其中n为正整数。

二、解决的思路
当N=1时,矩阵为;
当N=2时,矩阵为;
当N>2(N为偶数如N=4)时,矩阵为;
当N>2(N为奇数如N=5)时,矩阵为。
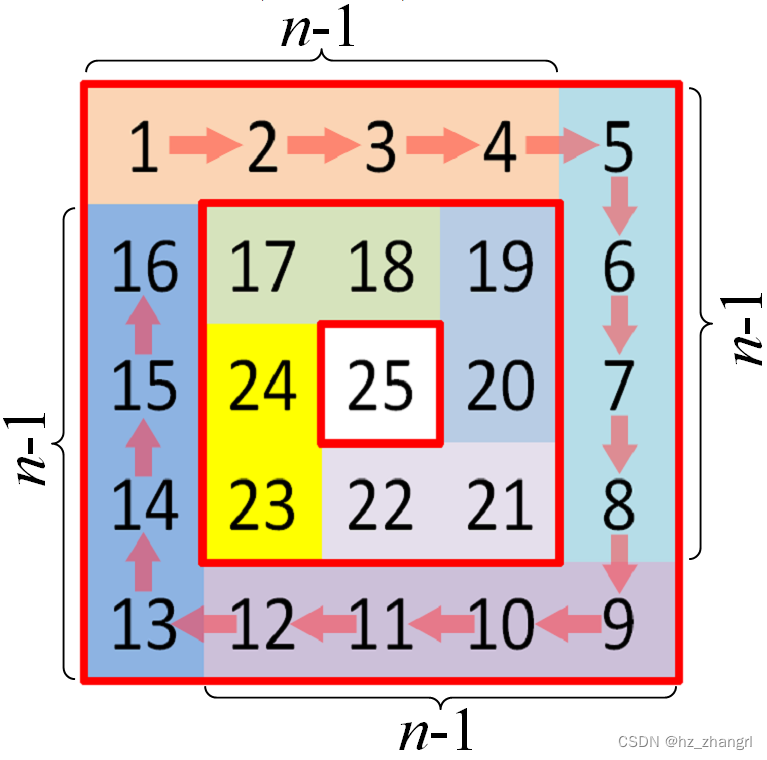
图1 螺旋矩阵分析图
三、递推法解题
从上思路分析和图1可知,当N>2时可分为k(k=N//2)个四边形的螺旋框,每边长为框长度(n)-1(即n-1),只是左上角的起始值和边框长度不同而已。如N为奇数,则正中心还有一个终值N²。
因此可用用递推来计算。
程序代码如下:
N = 5
def prt(b): # 打印二维列表
for i in range(N):
for j in range(N):
print("%3d" % b[i][j], end='')
print()
def Helix_Matrix(N):
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
matrix[N//2][N//2] = N*N # 若N为奇数时,正中间为N²
cnt = 0
n = N
for k in range(N//2):
for j in range(n-1): # 矩形上边,从左向右
cnt += 1
matrix[k][k+j] = cnt
for i in range(n-1): # 矩形右边,从上往下
cnt += 1
matrix[k+i][k+n-1] = cnt
for j in range(n-1): # 矩形下边,从右向左
cnt += 1
matrix[k+n-1][k+n-1-j] = cnt
for i in range(n-1): # 矩形左边,从下往上
cnt += 1
matrix[k+n-1-i][k] = cnt
n -= 2 # 缩小规模时,矩形边长减2
return matrix
hm = Helix_Matrix(N)
prt(hm)执行结果:
| 1 | 2 | 3 | 4 | 5 |
| 16 | 17 | 18 | 19 | 6 |
| 15 | 24 | 25 | 20 | 7 |
| 14 | 23 | 22 | 21 | 8 |
| 13 | 12 | 11 | 10 | 9 |
回到开头的题目,则
def Helix_Matrix(N):
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
matrix[N//2][N//2] = N*N # 若N为奇数时,正中间为N²
cnt = 0
n = N
for k in range(N//2):
for j in range(n-1): # 矩形上边,从左向右
cnt += 1
matrix[k][k+j] = cnt
for i in range(n-1): # 矩形右边,从上往下
cnt += 1
matrix[k+i][k+n-1] = cnt
for j in range(n-1): # 矩形下边,从右向左
cnt += 1
matrix[k+n-1][k+n-1-j] = cnt
for i in range(n-1): # 矩形左边,从下往上
cnt += 1
matrix[k+n-1-i][k] = cnt
n -= 2 # 缩小规模时,矩形边长减2
return matrix
n, i, j = map(int,input().split())
hm = Helix_Matrix(n)
print(hm[i-1][j-1])输入4 2 3,输出为14。
四、递归法解题
当规模为1时直接填写(1个元素),见“二、解决的思路”,结束递归;
当规模为2时直接填写(4个元素),见“二、解决的思路”,结束递归;
当规模大于2时直接先写本圈(k)四边,见“二、解决的思路”,再缩小规模递归调用。
这就是递归计算算法。
程序代码如下:
N = 6
def prt(b): # 打印二维列表
for i in range(N):
for j in range(N):
print("%3d" % b[i][j], end='')
print()
def Helix_Matrix(n,k,cnt):
if n == 1: # 规模为1
matrix[k][k] = cnt
elif n == 2: # 规模为2
matrix[k][k] = cnt
cnt += 1
matrix[k][k+1] = cnt
cnt += 1
matrix[k+1][k+1] = cnt
cnt += 1
matrix[k+1][k] = cnt
else: # 规模大于2
for j in range(n-1): # 矩形上边,由左向右
matrix[k][k+j] = cnt
cnt += 1
for i in range(n-1): # 矩形右边,由上往下
matrix[k+i][k+n-1] = cnt
cnt += 1
for j in range(n-1): # 矩形下边,由右向左
matrix[k+n-1][k+n-1-j] = cnt
cnt += 1
for i in range(n-1): # 矩形左边,由下往上
matrix[k+n-1-i][k] = cnt
cnt += 1
Helix_Matrix(n-2, k + 1, cnt) # 递归,缩小螺旋矩阵规模
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
Helix_Matrix(N,0,1) # 初始n=N, k=0, cnt=1
prt(matrix)执行结果:
| 1 | 2 | 3 | 4 | 5 | 6 |
| 20 | 21 | 22 | 23 | 24 | 7 |
| 19 | 32 | 33 | 34 | 25 | 8 |
| 18 | 31 | 36 | 35 | 26 | 9 |
| 17 | 30 | 29 | 28 | 27 | 10 |
| 16 | 15 | 14 | 13 | 12 | 11 |
回到开头的题目,则
def Helix_Matrix(n,k,cnt):
if n == 1: # 规模为1
matrix[k][k] = cnt
elif n == 2: # 规模为2
matrix[k][k] = cnt
cnt += 1
matrix[k][k+1] = cnt
cnt += 1
matrix[k+1][k+1] = cnt
cnt += 1
matrix[k+1][k] = cnt
else: # 规模大于2
for j in range(n-1): # 矩形上边,由左向右
matrix[k][k+j] = cnt
cnt += 1
for i in range(n-1): # 矩形右边,由上往下
matrix[k+i][k+n-1] = cnt
cnt += 1
for j in range(n-1): # 矩形下边,由右向左
matrix[k+n-1][k+n-1-j] = cnt
cnt += 1
for i in range(n-1): # 矩形左边,由下往上
matrix[k+n-1-i][k] = cnt
cnt += 1
Helix_Matrix(n-2, k + 1, cnt) # 递归,缩小螺旋矩阵规模
N, x, y = map(int,input().split())
matrix = [] # 初始化二维矩阵matrix(二维列表)
for i in range(N):
matrix.append([])
for j in range(N):
matrix[i].append(0)
Helix_Matrix(N,0,1) # 初始n=N, k=0, cnt=1
print(matrix[x-1][y-1])输入4 2 3,输出为14。