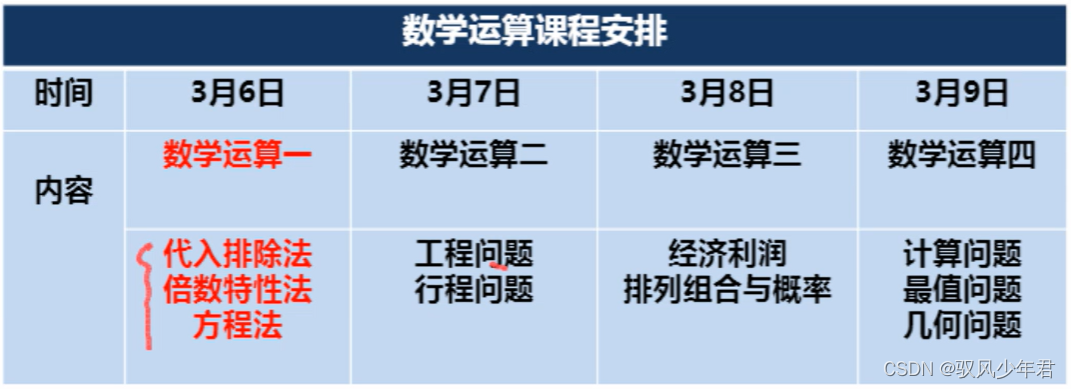
一、代入排除法

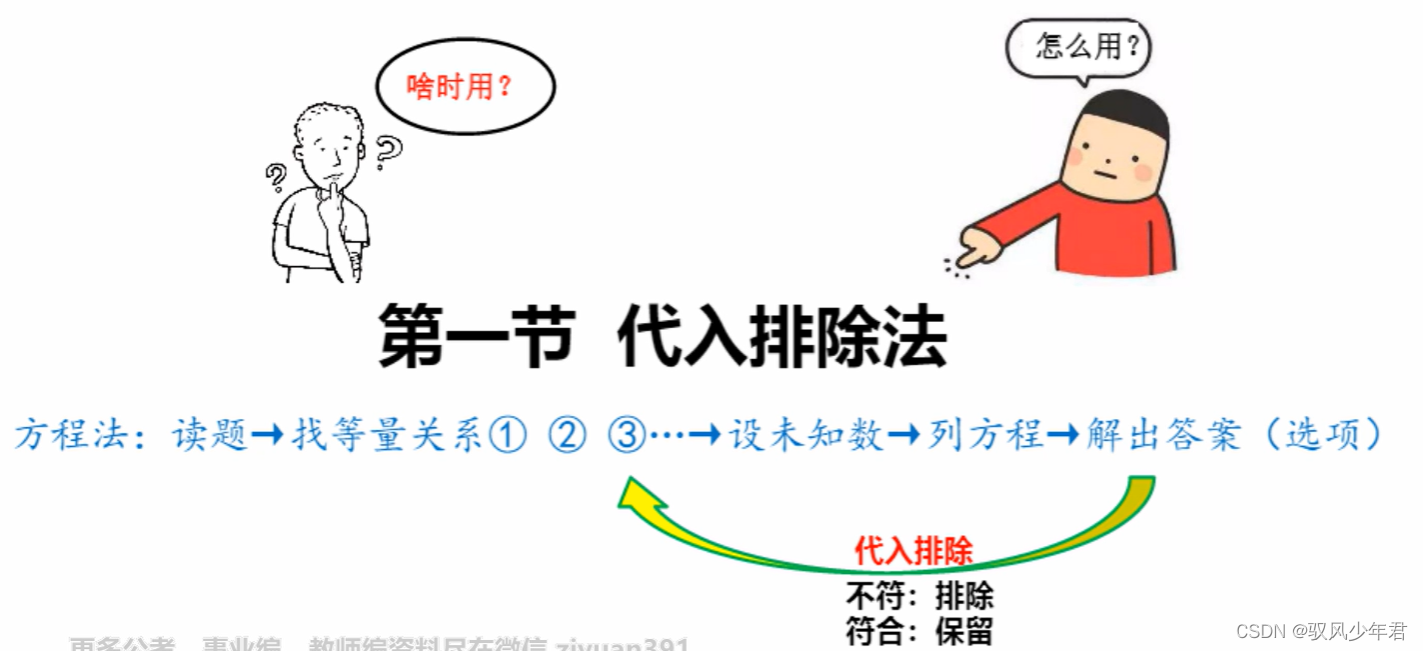
1.什么时候使用——

优先考虑常见题型

2.选项信息充分

3. 难题

2.怎么用

先排除不符合条件，再代入。

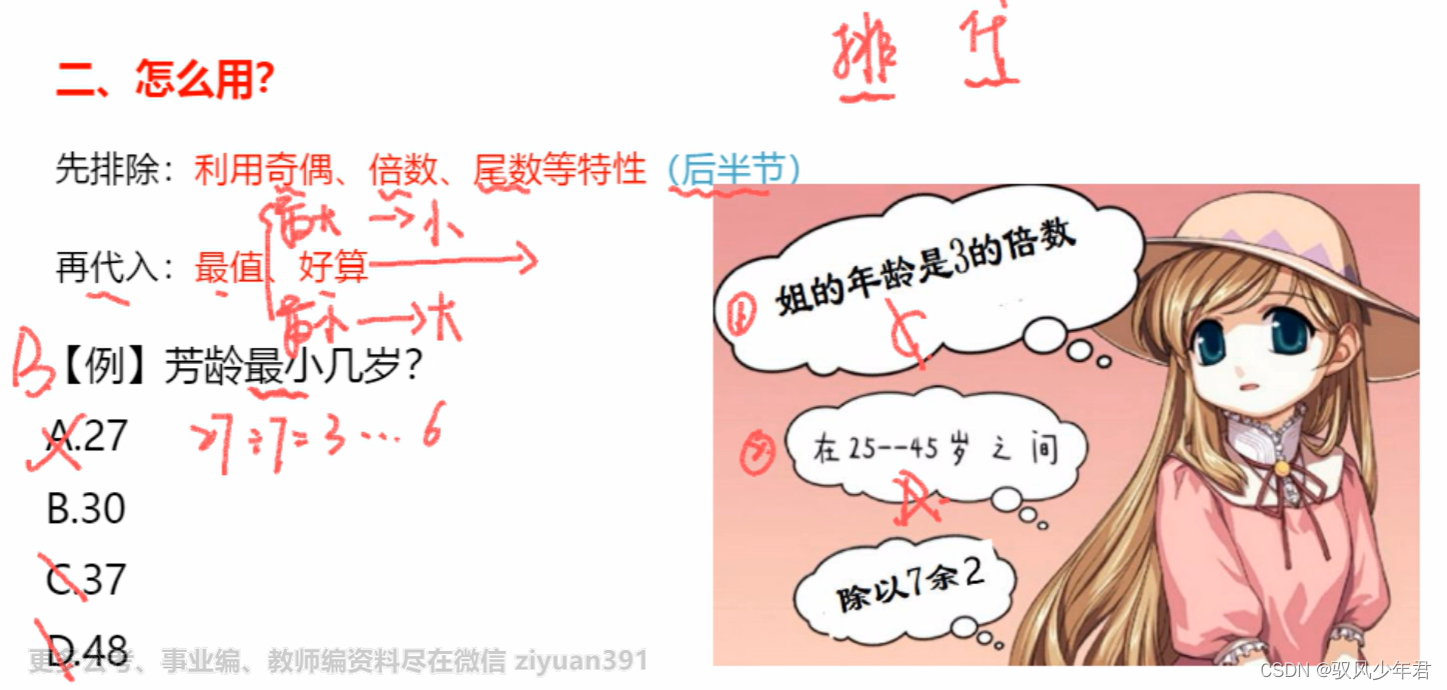
例题

问的是最多，最值原则，从大到小去代入。

总结

二、倍数特性（福建爱考）_a余数型_b倍数型

(利用条件中的倍数，排除答案)

2.1余数型

多退少补

例题——平均分组有剩余

平均分组有剩余——余数型
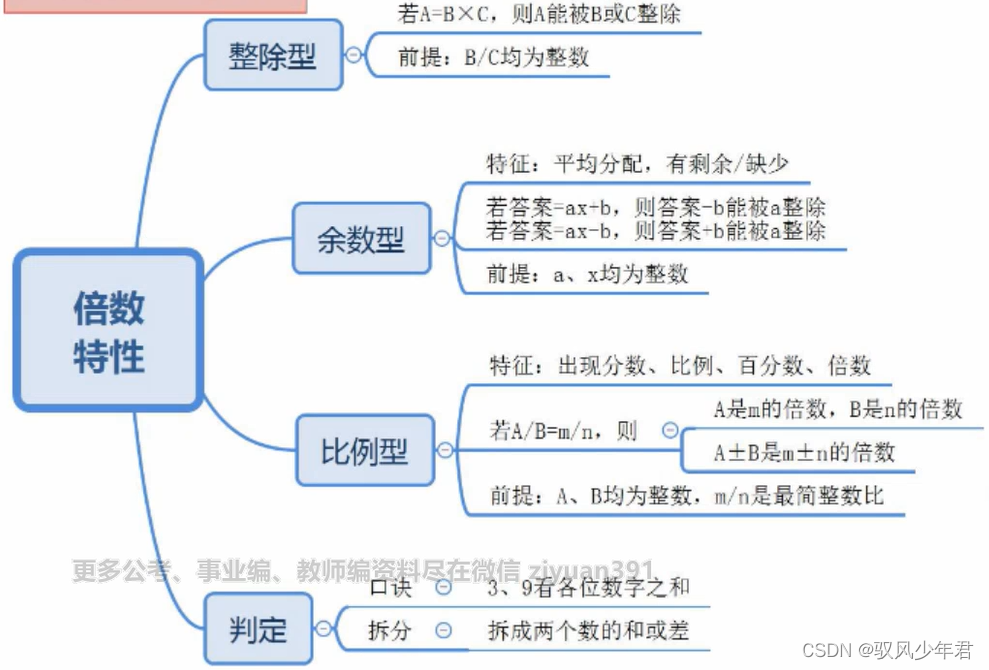
2的倍数——偶数，5 的倍数——0,5截位，3/9倍数——各位数之和为3/9的倍数；能被3整除，不一定能被9整除——12345
其他数就直接除，或者拆开相应倍数的值相加或者相减得到——119=70+49——7的倍数

倍数互斥传递原理
一个数既是2的倍数，又是5的倍数，说明这个数要是10的倍数
一个数既是2的倍数，又是3的倍数，说明这个数要是6的倍数
一个数既是5的倍数，又是6的倍数，说明这个数要是30的倍数
不互斥，一个数既是2的倍数，又是4的倍数,2和4的包含关系，所以这个数的4的倍数就可以。

2.2 比例型

比例型要化为最简整数比



谁比谁,谁除以谁，比谁多，就多谁的倍数
少，1-；
多，1+；

出现倍数，优先考虑引用倍数型，多几倍需要加1

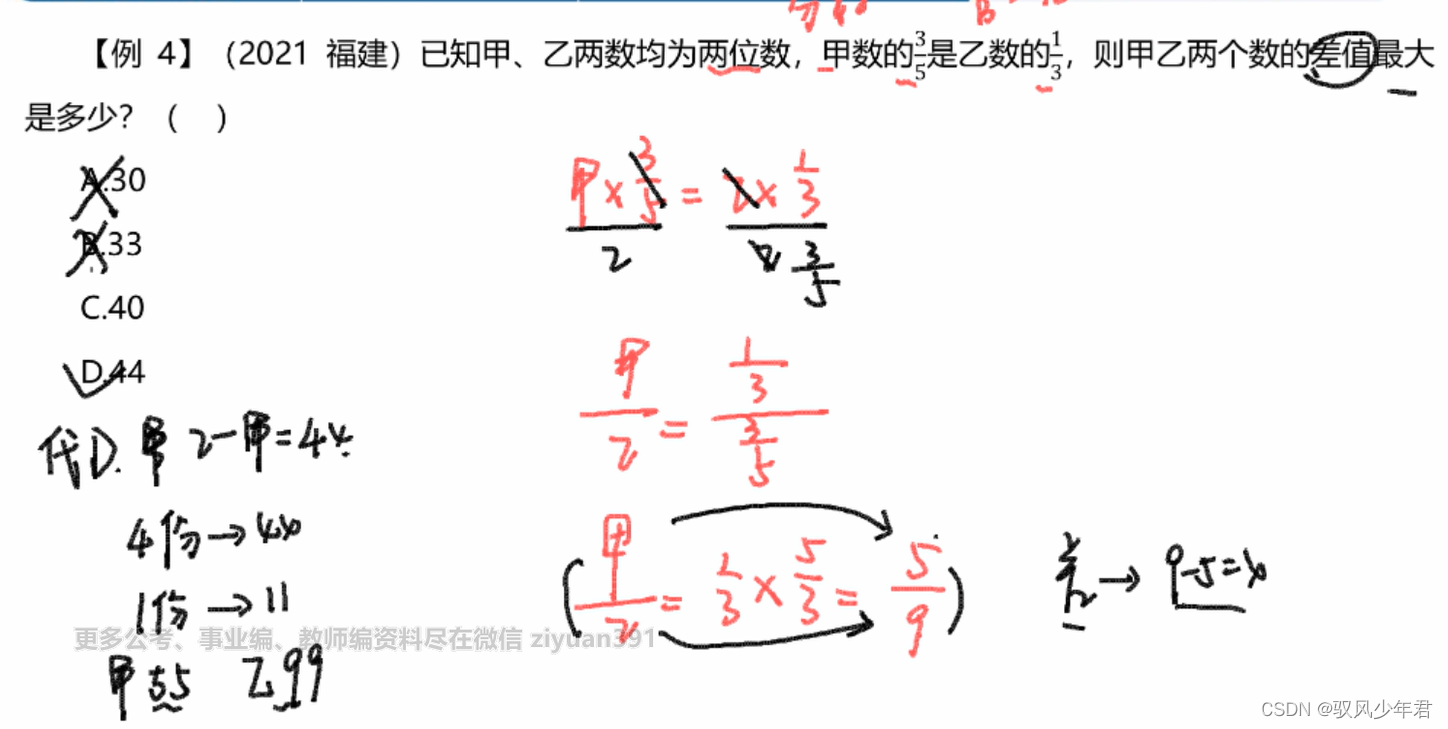
化最简找到，与问题相关的，不能解决曲线救国，找到比较大的化简分数，猜测对应的数。

总结

①想:看到佘数、比例想倍数特性
②看:看问题求谁
③干:用倍数特性盘它

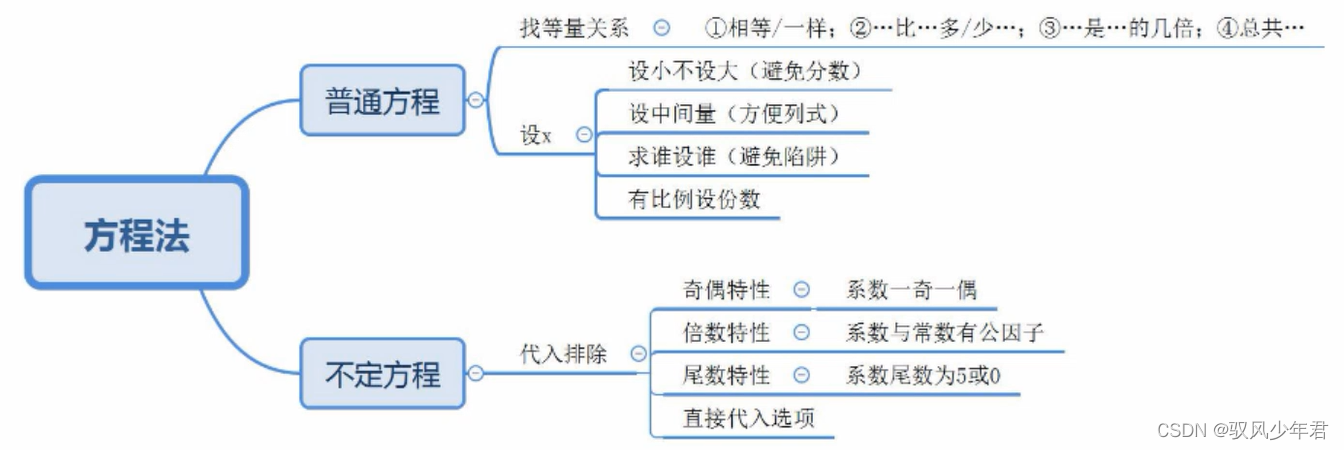
3.方程法

3.1 普通方程

设未知数，设小不设大，设中间量，有比例设分数，问谁设谁

看到百分数，先考虑倍数特性，出现百分数，可以设置总人数为100x

3.2 不定方程

不定方程，就是无法求解，只能结合选项和条件，进行排除。

倍数特性

系数其中之一与常数有公因子时候

奇偶特性

偶数倍必是偶数，奇数倍不确定→先从数倍下手，反推奇数倍

尾数特性

通过确定的一个尾数，去反推另一个因子的尾数

总结

尾数，可以不用化简，另外两个需要化简

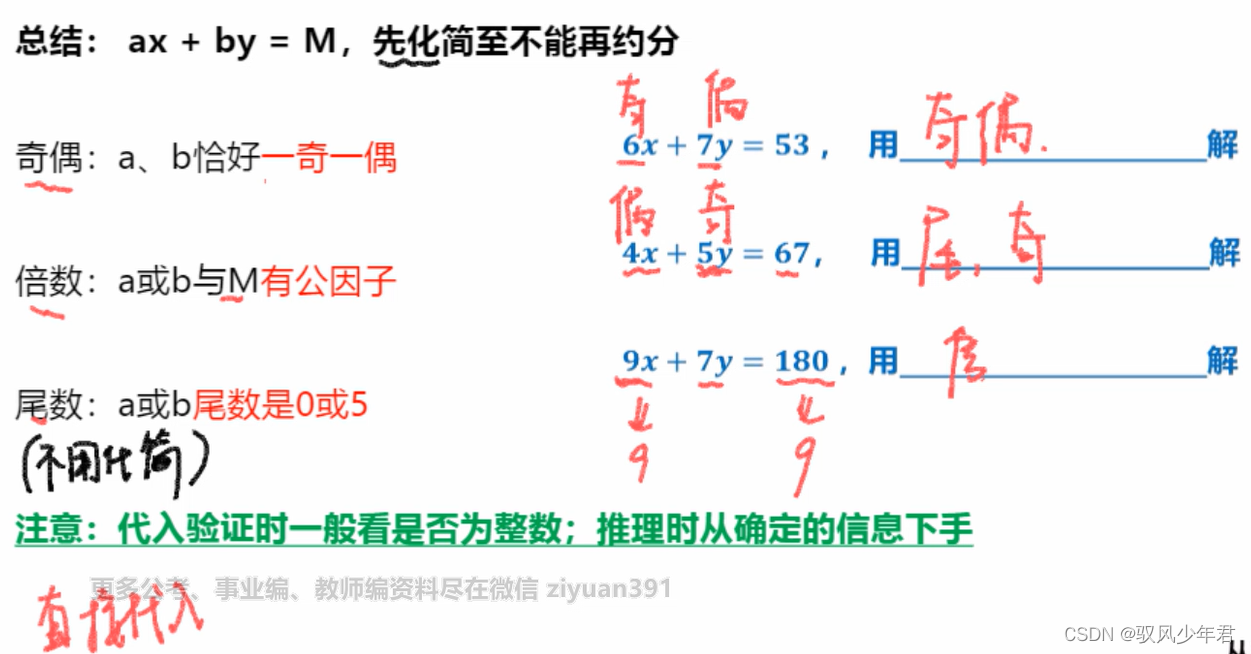
例题

这道题，需要先化简，尾数不需要，可以用到奇偶性（一奇数一偶数），尾数特性（0,5），直接代入
选项直接给出x，和y等未知数的值，直接带入更快

3.3不定方程组

未知数是整数（人等）——消元法

未知数是人，所以先消元，再用特性求解

未知数不一定是整数（钱和公里等）——赋0法

未知数不一定是整数，求x，y，z的总和
可以令系数最大的值为0，进行解方程


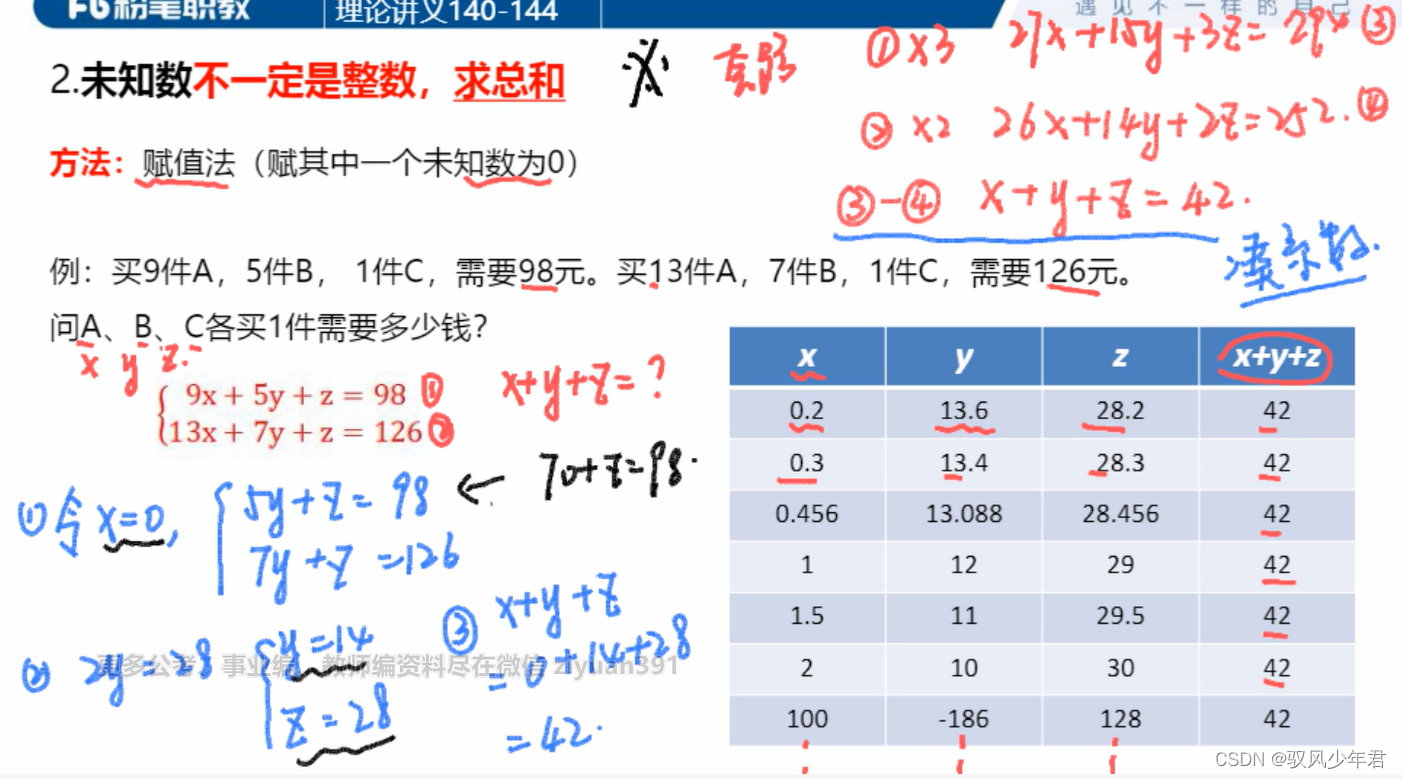
三个系数，两个和，求三个未知数之和

总结