目录
一、CEC2009无约束多目标测试集
二、CEC2009无约束多目标测试集UF1-UF10Matlab代码
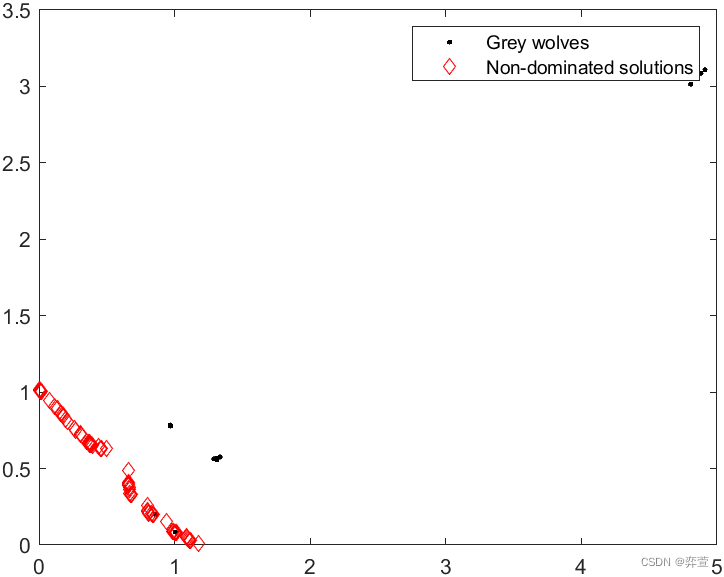
三、多目标灰狼算法测试CEC2009无约束多目标测试集
一、CEC2009无约束多目标测试集
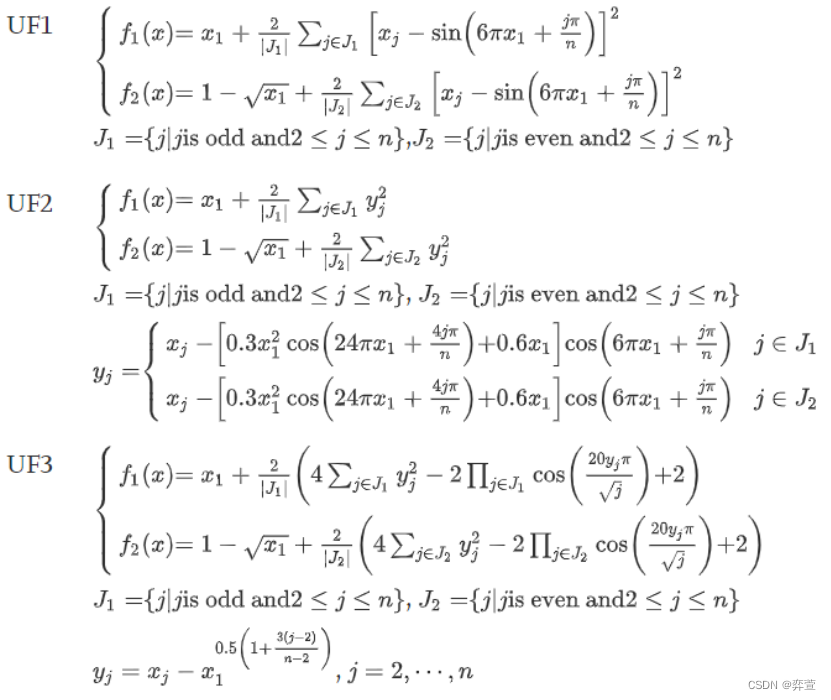
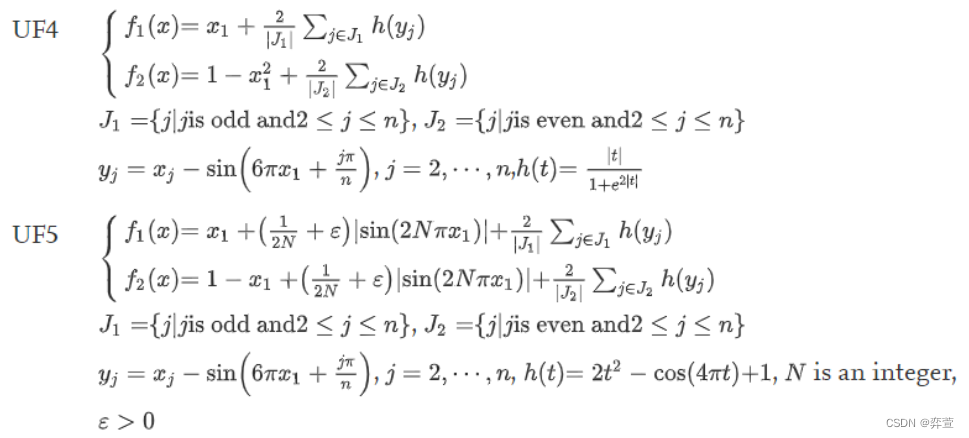


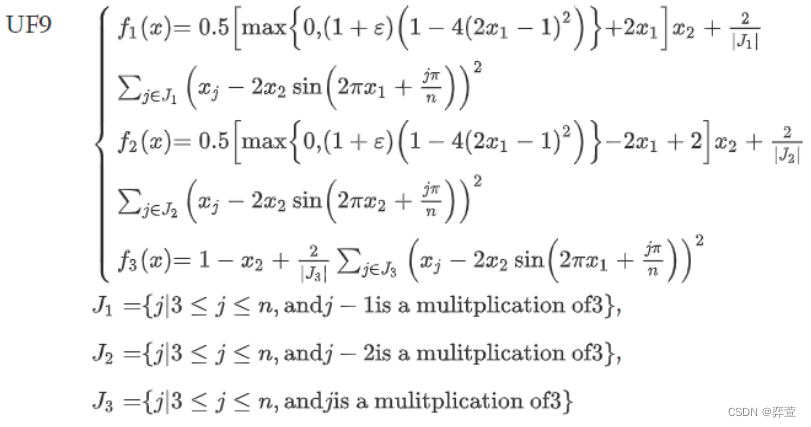

二、CEC2009无约束多目标测试集UF1-UF10Matlab代码
% cec09.m
% The Matlab version of the test instances for CEC 2009 Multiobjective
% Optimization Competition.
function fobj = cec09(name)
switch name
case 'UF1'
fobj = @UF1;
case 'UF2'
fobj = @UF2;
case 'UF3'
fobj = @UF3;
case 'UF4'
fobj = @UF4;
case 'UF5'
fobj = @UF5;
case 'UF6'
fobj = @UF6;
case 'UF7'
fobj = @UF7;
case 'UF8'
fobj = @UF8;
case 'UF9'
fobj = @UF9;
case 'UF10'
fobj = @UF10;
case 'CF1'
fobj = @CF1;
case 'CF2'
fobj = @CF2;
case 'CF3'
fobj = @CF3;
case 'CF4'
fobj = @CF4;
case 'CF5'
fobj = @CF5;
case 'CF6'
fobj = @CF6;
case 'CF7'
fobj = @CF7;
case 'CF8'
fobj = @CF8;
case 'CF9'
fobj = @CF9;
case 'CF10'
fobj = @CF10;
otherwise
fobj = @UF1;
end
end
%% UF1
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF1(x)
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;
tmp1 = sum(tmp(3:2:dim,:)); % odd index
tmp2 = sum(tmp(2:2:dim,:)); % even index
y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
clear tmp;
end
%% UF2
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF2(x)
[dim, num] = size(x);
X1 = repmat(x(1,:),[dim-1,1]);
A = 6*pi*X1 + pi/dim*repmat((2:dim)',[1,num]);
tmp = zeros(dim,num);
tmp(2:dim,:)= (x(2:dim,:) - 0.3*X1.*(X1.*cos(4.0*A)+2.0).*cos(A)).^2;
tmp1 = sum(tmp(3:2:dim,:)); % odd index
tmp(2:dim,:)= (x(2:dim,:) - 0.3*X1.*(X1.*cos(4.0*A)+2.0).*sin(A)).^2;
tmp2 = sum(tmp(2:2:dim,:)); % even index
y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
clear X1 A tmp;
end
%% UF3
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF3(x)
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = x(2:dim,:) - repmat(x(1,:),[dim-1,1]).^(0.5+1.5*(repmat((2:dim)',[1,num])-2.0)/(dim-2.0));
tmp1 = zeros(dim,num);
tmp1(2:dim,:)= Y(2:dim,:).^2;
tmp2 = zeros(dim,num);
tmp2(2:dim,:)= cos(20.0*pi*Y(2:dim,:)./sqrt(repmat((2:dim)',[1,num])));
tmp11 = 4.0*sum(tmp1(3:2:dim,:)) - 2.0*prod(tmp2(3:2:dim,:)) + 2.0; % odd index
tmp21 = 4.0*sum(tmp1(2:2:dim,:)) - 2.0*prod(tmp2(2:2:dim,:)) + 2.0; % even index
y(1,:) = x(1,:) + 2.0*tmp11/size(3:2:dim,2);
y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp21/size(2:2:dim,2);
clear Y tmp1 tmp2;
end
%% UF4
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF4(x)
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
H = zeros(dim,num);
H(2:dim,:) = abs(Y(2:dim,:))./(1.0+exp(2.0*abs(Y(2:dim,:))));
tmp1 = sum(H(3:2:dim,:)); % odd index
tmp2 = sum(H(2:2:dim,:)); % even index
y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - x(1,:).^2 + 2.0*tmp2/size(2:2:dim,2);
clear Y H;
end
%% UF5
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF5(x)
N = 10.0;
E = 0.1;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
H = zeros(dim,num);
H(2:dim,:) = 2.0*Y(2:dim,:).^2 - cos(4.0*pi*Y(2:dim,:)) + 1.0;
tmp1 = sum(H(3:2:dim,:)); % odd index
tmp2 = sum(H(2:2:dim,:)); % even index
tmp = (0.5/N+E)*abs(sin(2.0*N*pi*x(1,:)));
y(1,:) = x(1,:) + tmp + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - x(1,:)+ tmp + 2.0*tmp2/size(2:2:dim,2);
clear Y H;
end
%% UF6
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF6(x)
N = 2.0;
E = 0.1;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = zeros(dim,num);
tmp1(2:dim,:)= Y(2:dim,:).^2;
tmp2 = zeros(dim,num);
tmp2(2:dim,:)= cos(20.0*pi*Y(2:dim,:)./sqrt(repmat((2:dim)',[1,num])));
tmp11 = 4.0*sum(tmp1(3:2:dim,:)) - 2.0*prod(tmp2(3:2:dim,:)) + 2.0; % odd index
tmp21 = 4.0*sum(tmp1(2:2:dim,:)) - 2.0*prod(tmp2(2:2:dim,:)) + 2.0; % even index
tmp = max(0,(1.0/N+2.0*E)*sin(2.0*N*pi*x(1,:)));
y(1,:) = x(1,:) + tmp + 2.0*tmp11/size(3:2:dim,2);
y(2,:) = 1.0 - x(1,:) + tmp + 2.0*tmp21/size(2:2:dim,2);
clear Y tmp1 tmp2;
end
%% UF7
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF7(x)
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;
tmp1 = sum(Y(3:2:dim,:)); % odd index
tmp2 = sum(Y(2:2:dim,:)); % even index
tmp = (x(1,:)).^0.2;
y(1,:) = tmp + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - tmp + 2.0*tmp2/size(2:2:dim,2);
clear Y;
end
%% UF8
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF8(x)
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = (x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]))).^2;
tmp1 = sum(Y(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(Y(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(Y(3:3:dim,:)); % j-0 = 3*k
y(1,:) = cos(0.5*pi*x(1,:)).*cos(0.5*pi*x(2,:)) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = cos(0.5*pi*x(1,:)).*sin(0.5*pi*x(2,:)) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = sin(0.5*pi*x(1,:)) + 2.0*tmp3/size(3:3:dim,2);
clear Y;
end
%% UF9
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF9(x)
E = 0.1;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = (x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]))).^2;
tmp1 = sum(Y(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(Y(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(Y(3:3:dim,:)); % j-0 = 3*k
tmp = max(0,(1.0+E)*(1-4.0*(2.0*x(1,:)-1).^2));
y(1,:) = 0.5*(tmp+2*x(1,:)).*x(2,:) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = 0.5*(tmp-2*x(1,:)+2.0).*x(2,:) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = 1-x(2,:) + 2.0*tmp3/size(3:3:dim,2);
clear Y;
end
%% UF10
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function y = UF10(x)
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]));
H = zeros(dim,num);
H(3:dim,:) = 4.0*Y(3:dim,:).^2 - cos(8.0*pi*Y(3:dim,:)) + 1.0;
tmp1 = sum(H(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(H(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(H(3:3:dim,:)); % j-0 = 3*k
y(1,:) = cos(0.5*pi*x(1,:)).*cos(0.5*pi*x(2,:)) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = cos(0.5*pi*x(1,:)).*sin(0.5*pi*x(2,:)) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = sin(0.5*pi*x(1,:)) + 2.0*tmp3/size(3:3:dim,2);
clear Y H;
end
%% CF1
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF1(x)
a = 1.0;
N = 10.0;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = (x(2:dim,:) - repmat(x(1,:),[dim-1,1]).^(0.5+1.5*(repmat((2:dim)',[1,num])-2.0)/(dim-2.0))).^2;
tmp1 = sum(Y(3:2:dim,:));% odd index
tmp2 = sum(Y(2:2:dim,:));% even index
y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - x(1,:) + 2.0*tmp2/size(2:2:dim,2);
c(1,:) = y(1,:) + y(2,:) - a*abs(sin(N*pi*(y(1,:)-y(2,:)+1.0))) - 1.0;
clear Y;
end
%% CF2
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF2(x)
a = 1.0;
N = 2.0;
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= (x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;
tmp1 = sum(tmp(3:2:dim,:)); % odd index
tmp(2:dim,:)= (x(2:dim,:) - cos(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]))).^2;
tmp2 = sum(tmp(2:2:dim,:)); % even index
y(1,:) = x(1,:) + 2.0*tmp1/size(3:2:dim,2);
y(2,:) = 1.0 - sqrt(x(1,:)) + 2.0*tmp2/size(2:2:dim,2);
t = y(2,:) + sqrt(y(1,:)) - a*sin(N*pi*(sqrt(y(1,:))-y(2,:)+1.0)) - 1.0;
c(1,:) = sign(t).*abs(t)./(1.0+exp(4.0*abs(t)));
clear tmp;
end
%% CF3
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF3(x)
a = 1.0;
N = 2.0;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(2:dim,:) = x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = zeros(dim,num);
tmp1(2:dim,:)= Y(2:dim,:).^2;
tmp2 = zeros(dim,num);
tmp2(2:dim,:)= cos(20.0*pi*Y(2:dim,:)./sqrt(repmat((2:dim)',[1,num])));
tmp11 = 4.0*sum(tmp1(3:2:dim,:)) - 2.0*prod(tmp2(3:2:dim,:)) + 2.0; % odd index
tmp21 = 4.0*sum(tmp1(2:2:dim,:)) - 2.0*prod(tmp2(2:2:dim,:)) + 2.0; % even index
y(1,:) = x(1,:) + 2.0*tmp11/size(3:2:dim,2);
y(2,:) = 1.0 - x(1,:).^2 + 2.0*tmp21/size(2:2:dim,2);
c(1,:) = y(2,:) + y(1,:).^2 - a*sin(N*pi*(y(1,:).^2-y(2,:)+1.0)) - 1.0;
clear Y tmp1 tmp2;
end
%% CF4
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF4(x)
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = sum(tmp(3:2:dim,:).^2); % odd index
tmp2 = sum(tmp(4:2:dim,:).^2); % even index
index1 = tmp(2,:) < (1.5-0.75*sqrt(2.0));
index2 = tmp(2,:)>= (1.5-0.75*sqrt(2.0));
tmp(2,index1) = abs(tmp(2,index1));
tmp(2,index2) = 0.125 + (tmp(2,index2)-1.0).^2;
y(1,:) = x(1,:) + tmp1;
y(2,:) = 1.0 - x(1,:) + tmp(2,:) + tmp2;
t = x(2,:) - sin(6.0*pi*x(1,:)+2.0*pi/dim) - 0.5*x(1,:) + 0.25;
c(1,:) = sign(t).*abs(t)./(1.0+exp(4.0*abs(t)));
clear tmp index1 index2;
end
%% CF5
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF5(x)
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= x(2:dim,:) - 0.8*repmat(x(1,:),[dim-1,1]).*cos(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = sum(2.0*tmp(3:2:dim,:).^2-cos(4.0*pi*tmp(3:2:dim,:))+1.0); % odd index
tmp(2:dim,:)= x(2:dim,:) - 0.8*repmat(x(1,:),[dim-1,1]).*sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp2 = sum(2.0*tmp(4:2:dim,:).^2-cos(4.0*pi*tmp(4:2:dim,:))+1.0); % even index
index1 = tmp(2,:) < (1.5-0.75*sqrt(2.0));
index2 = tmp(2,:)>= (1.5-0.75*sqrt(2.0));
tmp(2,index1) = abs(tmp(2,index1));
tmp(2,index2) = 0.125 + (tmp(2,index2)-1.0).^2;
y(1,:) = x(1,:) + tmp1;
y(2,:) = 1.0 - x(1,:) + tmp(2,:) + tmp2;
c(1,:) = x(2,:) - 0.8*x(1,:).*sin(6.0*pi*x(1,:)+2.0*pi/dim) - 0.5*x(1,:) + 0.25;
clear tmp;
end
%% CF6
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF6(x)
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= x(2:dim,:) - 0.8*repmat(x(1,:),[dim-1,1]).*cos(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = sum(tmp(3:2:dim,:).^2); % odd index
tmp(2:dim,:)= x(2:dim,:) - 0.8*repmat(x(1,:),[dim-1,1]).*sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp2 = sum(tmp(2:2:dim,:).^2); % even index
y(1,:) = x(1,:) + tmp1;
y(2,:) = (1.0 - x(1,:)).^2 + tmp2;
tmp = 0.5*(1-x(1,:))-(1-x(1,:)).^2;
c(1,:) = x(2,:) - 0.8*x(1,:).*sin(6.0*pi*x(1,:)+2*pi/dim) - sign(tmp).*sqrt(abs(tmp));
tmp = 0.25*sqrt(1-x(1,:))-0.5*(1-x(1,:));
c(2,:) = x(4,:) - 0.8*x(1,:).*sin(6.0*pi*x(1,:)+4*pi/dim) - sign(tmp).*sqrt(abs(tmp));
clear tmp;
end
%% CF7
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF7(x)
[dim, num] = size(x);
tmp = zeros(dim,num);
tmp(2:dim,:)= x(2:dim,:) - cos(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp1 = sum(2.0*tmp(3:2:dim,:).^2-cos(4.0*pi*tmp(3:2:dim,:))+1.0); % odd index
tmp(2:dim,:)= x(2:dim,:) - sin(6.0*pi*repmat(x(1,:),[dim-1,1]) + pi/dim*repmat((2:dim)',[1,num]));
tmp2 = sum(2.0*tmp(6:2:dim,:).^2-cos(4.0*pi*tmp(6:2:dim,:))+1.0); % even index
tmp(2,:) = tmp(2,:).^2;
tmp(4,:) = tmp(4,:).^2;
y(1,:) = x(1,:) + tmp1;
y(2,:) = (1.0 - x(1,:)).^2 + tmp(2,:) + tmp(4,:) + tmp2;
tmp = 0.5*(1-x(1,:))-(1-x(1,:)).^2;
c(1,:) = x(2,:) - sin(6.0*pi*x(1,:)+2*pi/dim) - sign(tmp).*sqrt(abs(tmp));
tmp = 0.25*sqrt(1-x(1,:))-0.5*(1-x(1,:));
c(2,:) = x(4,:) - sin(6.0*pi*x(1,:)+4*pi/dim) - sign(tmp).*sqrt(abs(tmp));
clear tmp;
end
%% CF8
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF8(x)
N = 2.0;
a = 4.0;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = (x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]))).^2;
tmp1 = sum(Y(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(Y(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(Y(3:3:dim,:)); % j-0 = 3*k
y(1,:) = cos(0.5*pi*x(1,:)).*cos(0.5*pi*x(2,:)) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = cos(0.5*pi*x(1,:)).*sin(0.5*pi*x(2,:)) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = sin(0.5*pi*x(1,:)) + 2.0*tmp3/size(3:3:dim,2);
c(1,:) = (y(1,:).^2+y(2,:).^2)./(1.0-y(3,:).^2) - a*abs(sin(N*pi*((y(1,:).^2-y(2,:).^2)./(1.0-y(3,:).^2)+1.0))) - 1.0;
clear Y;
end
%% CF9
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF9(x)
N = 2.0;
a = 3.0;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = (x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]))).^2;
tmp1 = sum(Y(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(Y(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(Y(3:3:dim,:)); % j-0 = 3*k
y(1,:) = cos(0.5*pi*x(1,:)).*cos(0.5*pi*x(2,:)) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = cos(0.5*pi*x(1,:)).*sin(0.5*pi*x(2,:)) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = sin(0.5*pi*x(1,:)) + 2.0*tmp3/size(3:3:dim,2);
c(1,:) = (y(1,:).^2+y(2,:).^2)./(1.0-y(3,:).^2) - a*sin(N*pi*((y(1,:).^2-y(2,:).^2)./(1.0-y(3,:).^2)+1.0)) - 1.0;
clear Y;
end
%% CF10
% x and y are columnwise, the imput x must be inside the search space and
% it could be a matrix
function [y,c] = CF10(x)
a = 1.0;
N = 2.0;
[dim, num] = size(x);
Y = zeros(dim,num);
Y(3:dim,:) = x(3:dim,:) - 2.0*repmat(x(2,:),[dim-2,1]).*sin(2.0*pi*repmat(x(1,:),[dim-2,1]) + pi/dim*repmat((3:dim)',[1,num]));
H = zeros(dim,num);
H(3:dim,:) = 4.0*Y(3:dim,:).^2 - cos(8.0*pi*Y(3:dim,:)) + 1.0;
tmp1 = sum(H(4:3:dim,:)); % j-1 = 3*k
tmp2 = sum(H(5:3:dim,:)); % j-2 = 3*k
tmp3 = sum(H(3:3:dim,:)); % j-0 = 3*k
y(1,:) = cos(0.5*pi*x(1,:)).*cos(0.5*pi*x(2,:)) + 2.0*tmp1/size(4:3:dim,2);
y(2,:) = cos(0.5*pi*x(1,:)).*sin(0.5*pi*x(2,:)) + 2.0*tmp2/size(5:3:dim,2);
y(3,:) = sin(0.5*pi*x(1,:)) + 2.0*tmp3/size(3:3:dim,2);
c(1,:) = (y(1,:).^2+y(2,:).^2)./(1.0-y(3,:).^2) - a*sin(N*pi*((y(1,:).^2-y(2,:).^2)./(1.0-y(3,:).^2)+1.0)) - 1.0;
clear Y H;
end三、多目标灰狼算法测试CEC2009无约束多目标测试集
UF2:
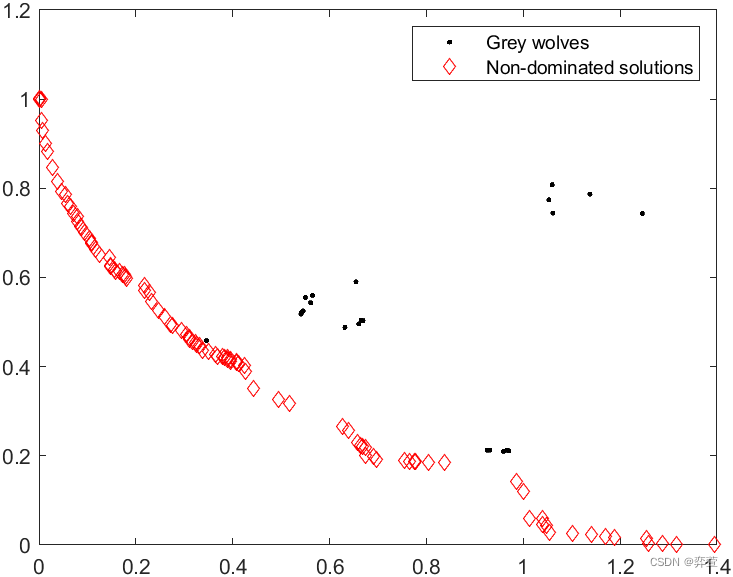
UF4:
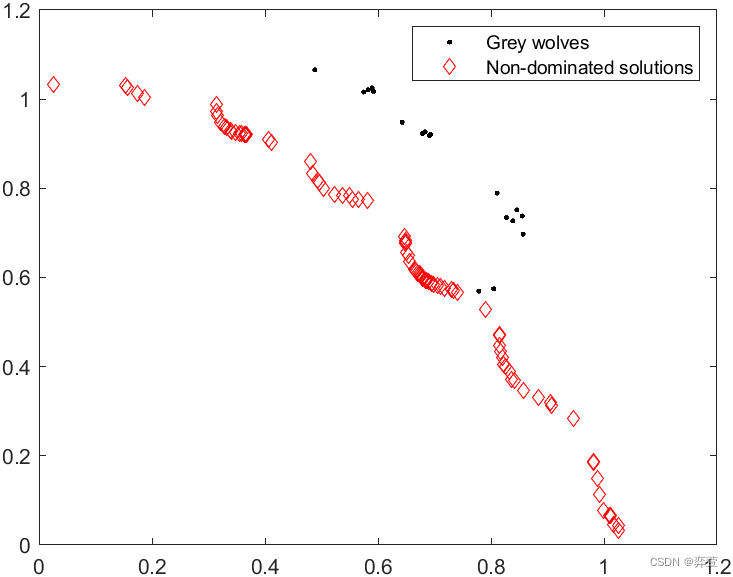
UF7: