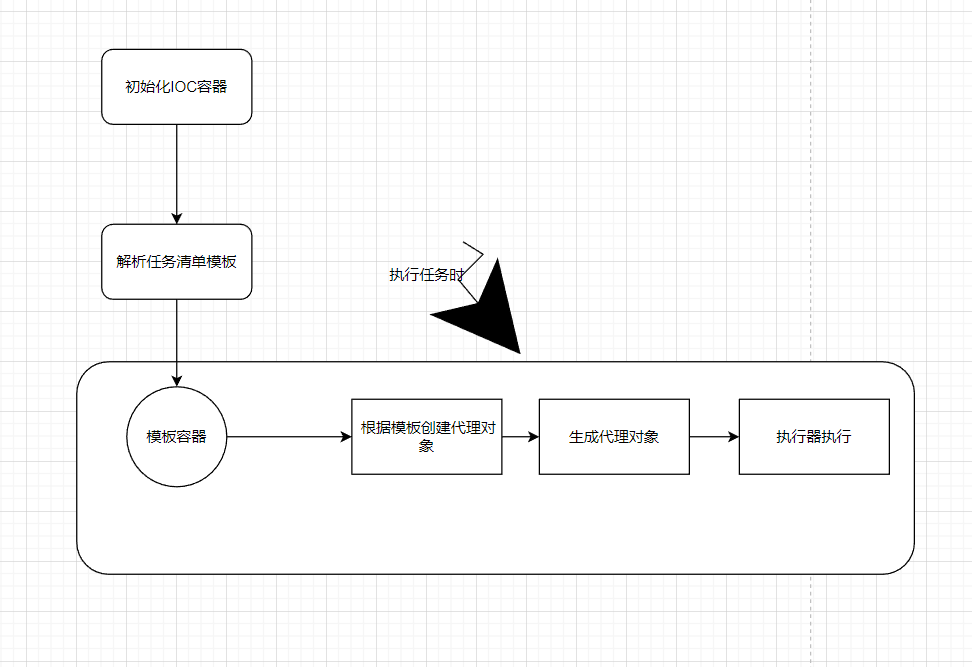
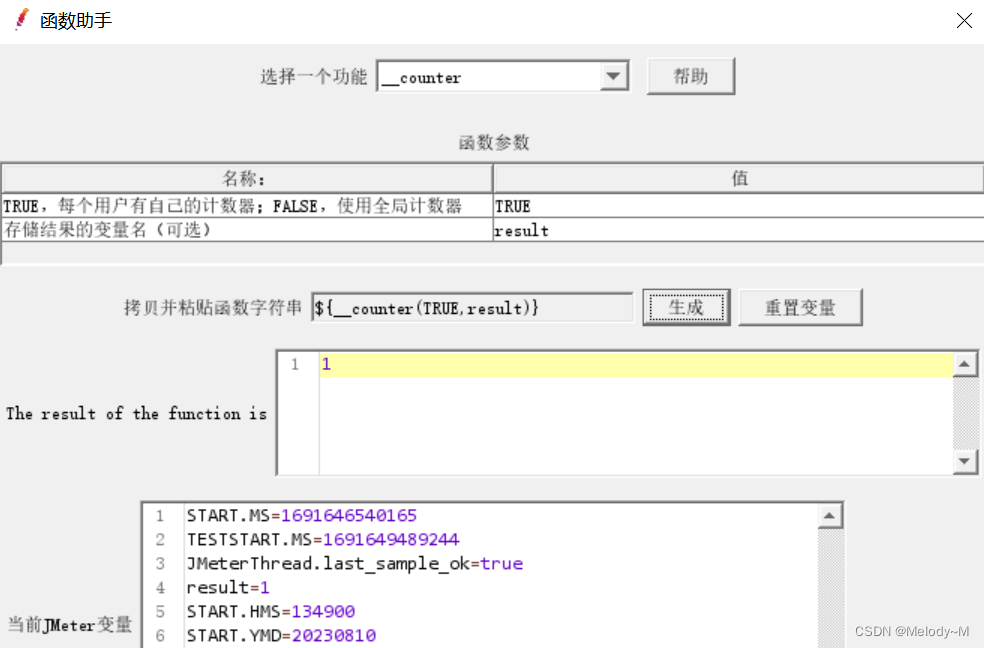
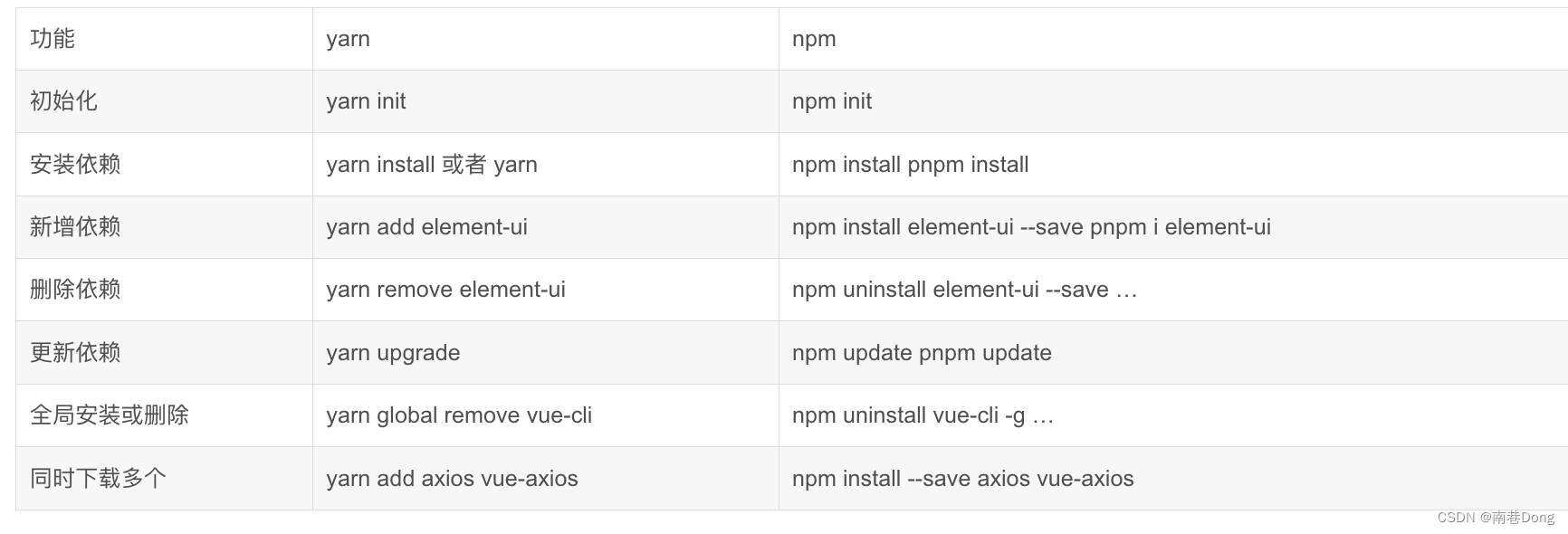
主要简介
1. 时间复杂度:运行一个程序所花费的时间。O()
2. 空间复杂度:运行程序所需要的内存 OOM,开了空间的地方, 比如 数组 链表,缓存对象,递归
时间复杂度表示方式
O(1),O(n),O(nlogn),O(n^2),O(n+1),O(logn),O(n!)
时间复杂度如何来分析
(1)找for while 递归。而且要找循环量最大的那一段
(2)同级循环怎么计算
几种常见的时间复杂度分析:指的是某一段代码。
计算时间复杂度 往往是计算比较大的 而且是不确定的数,如果已经确定了,那么就不用计算了,也是我们说的常量。
常数:O(1) 1表示是常数,所有能确定的数字我们都用O(1),O(1000)=>o(1)
对数:O(logn),O(nlogn)
线性:O(n)
线性对数:O(nlogn)
平方:O(n^2)
N次方:O(n^n)
我们怎么找时间复杂度:
1.找到有循环的地方,
2.找有网络请求(RPC,远程调用,分布式,数据库请求)的地方。
就是测试时间:log打印,计算平均时间。

几种常见的时间复杂度总结
学了时间复杂度,那我们的目的就是要把代码写到最优,效率最高;
O(1)>O(logn)>O(n)>O(nlogn)>O(n^2)>O(n^x)
O(1)>O(logn)>O(n)>O(nlogn) 效果都是很好的。几乎优化的空间不是很大。
登录:判断用户名密码O(1)到数据库里查记录;分布式 缓存。举例:要优化接口的话万一用的是冒泡排序,想要提升时间复杂度的话,就得知道冒泡排序的时间复杂度(O(n^2))。找更优秀的排序算法 快速排序O(n),归并排序O(nlogn),堆排序替代冒泡排序实现等等。
列表的接口:排序,冒泡排序;=>找更优秀的排序算法 快速排序,归并排序,堆排序。当然优化的目标就是要往O(1)的方向接近。
代码实例
package algorithm.time;
public class BigO11 {
public static void main(String[] args) {
int a = 1; //1次 O(1)
for(int i = 0 ;i < 3;i++){//这里会运行几次?4次 在第4次的时候结束 跳出 i=3 (0 1 2 3)
a = a + 1; //这里运行几次? 3次 O(1)? n+1 n 1 O(3)? => O(1)
}
int n = Integer.MAX_VALUE; //表示n是未知
int i = 1;
for(int j = 0 ; j < n ;j++){
while ( i <= n){
i = i * 2;
}
}
while( i <= n){
i = i * 3; //O(logn)
}
//i的值:2 4 8 16 32,=》2^0,2^1,2^2,2^3,.....2^n
//===> 2^x=n =>求出x就是我们运行的次数 => x=log2n =>计算机忽略掉常数 => x = logn =>O(logn)
//二分查找 为什么是logn的算法?
//1~100 找69这个数
//50:(1+100)/2 = 50
for(i = 0 ; i < n;i++){
a = a +1; //运行了多少次?O(n) n一定是一个未知的,如果n是已知6的
}
for(i = 0 ; i < n;i++){ // 乘法 n次
for(int j = 0 ; j < n ;j ++){ //n次
a = a +1; //运行了多少次? O(n^2)
}
}
for(i = 0 ; i < n;i++){ // 乘法 n次
for(int j = i ; j < n ;j ++){ //n次
a = a +1; //运行了多少次? n*(n+1)/2 => O(n^2); => (n^2+n)/2 => 注意有个规律,有加减法的时候,找次数最高的那个
}
}
/*
* 外面的循环次数是确定的 O(n) n次,1 2 3 4 。。。n
*
* i=n 运行1次
* i=n-1 运行2次
* .
* .
* .
* i=1 运行n次
*
* 1,2,3 …… n次 最后里面这层要运行多少次?1+2+3+……+n=n*(n+1)/2 =>
*
*/
}
}