写在前面
因为公司给的PCA结果效果不佳,决定从中重新挑选部分样本进行再分析
步骤
表格结果预处理
- 在属水平genus参考原本结果已有的PCA图,尽可能挑选距离较远且聚团的样本
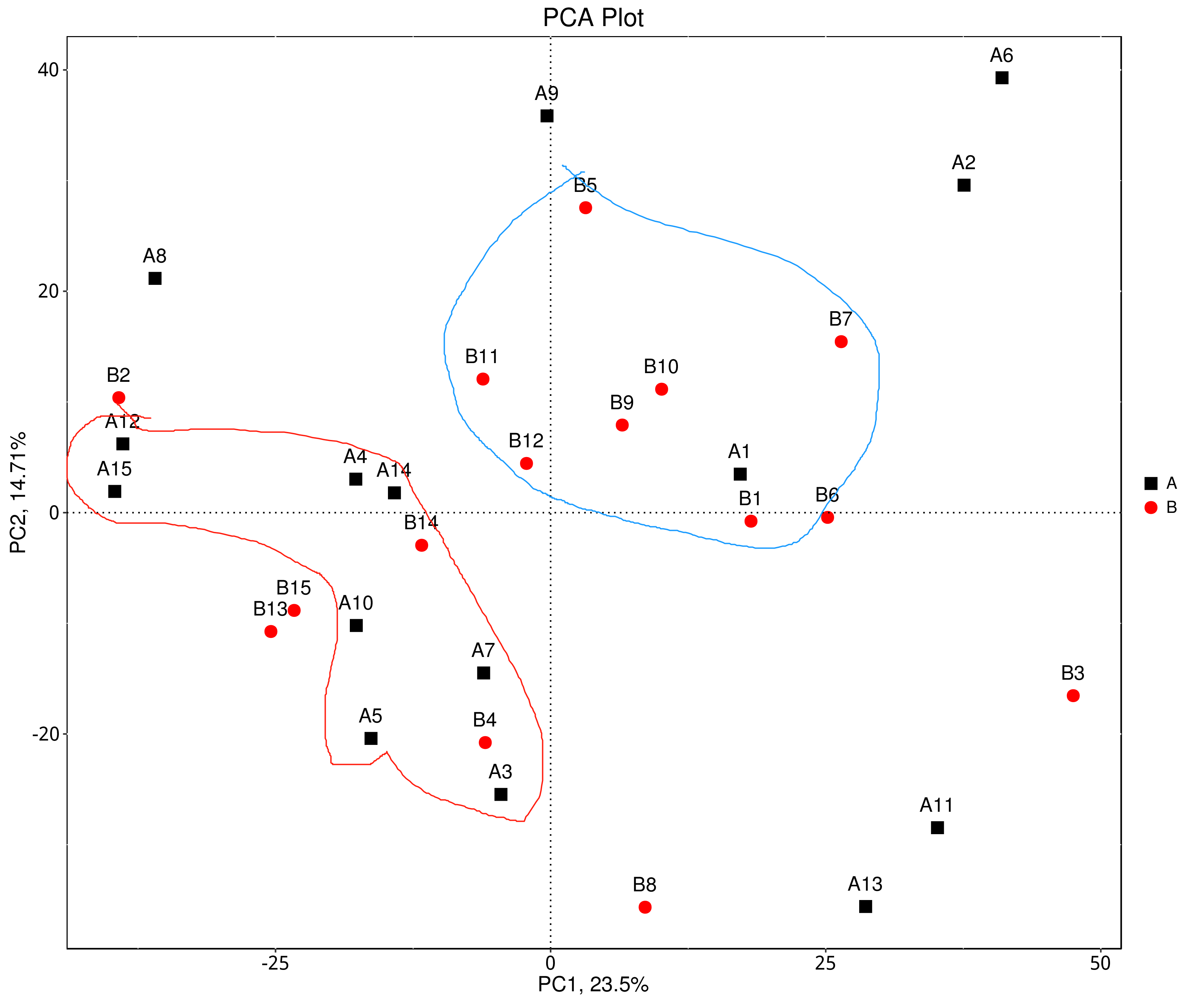
- 选取不同样本属水平的丰度数据,整理成逗号分隔的csv文件
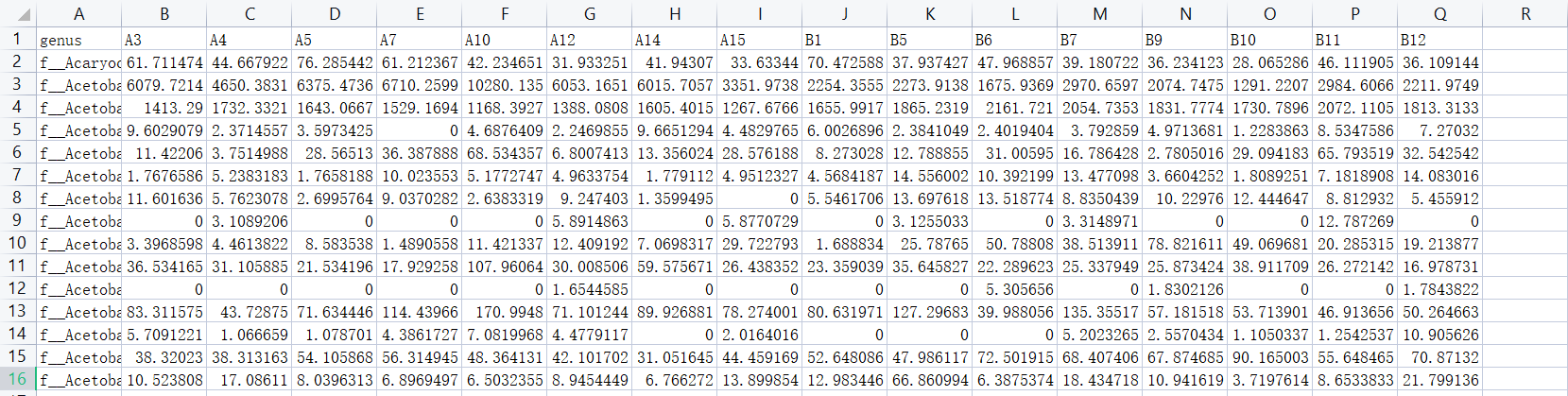
代码演示
library(vegan) # 计算bray距离
library(ggplot2)
library(tidyverse)
library(ape) # pcoa分析
## 如果没装先install.packages("vegan")等
genus_num <- read.table('F:/Analysis/RA_Sanhe cow/Microgenome/PCA/Demo_PCA.csv',row.names = 1,header = T, sep = ',') #地址注意反斜线,或者使用‘\\’反义
bray.dist = vegdist(t(genus_num), method="bray")
jay.h.pc <- pcoa(bray.dist)
#str(spe.h.pc)#记录一二轴解释率“Eigenvalues”
jay.h.pcoa <- jay.h.pc$vectors
jay.pcoa <- data.frame(jay.h.pcoa[,1:2]) %>%
mutate(Treatments = rep(c('A', 'B'), each = 8)) #根据列数分组,此处意思是前八列为A组,后八列为B组
# PERMANOVA置换多元方差分析
jay <- bray.dist
env <- select(jay.pcoa, Treatments)
#获取单因素的数据(方式一)
permanova <- adonis(jay ~ Treatments, data = env, permutations = 999,method="bray")
fcnames <- row.names(permanova$aov.tab)
lab <- paste('PERMANOVA\n',fcnames[1],':R^2=',round(permanova$aov.tab[1,5],4),' p=',
round(permanova$aov.tab[1,6],4), sep = '')
#获取单因素的数据(方式二)
permanova2 <- adonis2(jay ~ Treatments, data = env, permutations = 999,method="bray")
fcnames2 <- row.names(permanova2)
lab2 <- paste('PERMANOVA2\n',fcnames2[1],':R^2=',round(permanova2[1,3],4),' p=',
round(permanova2[1,5],4))
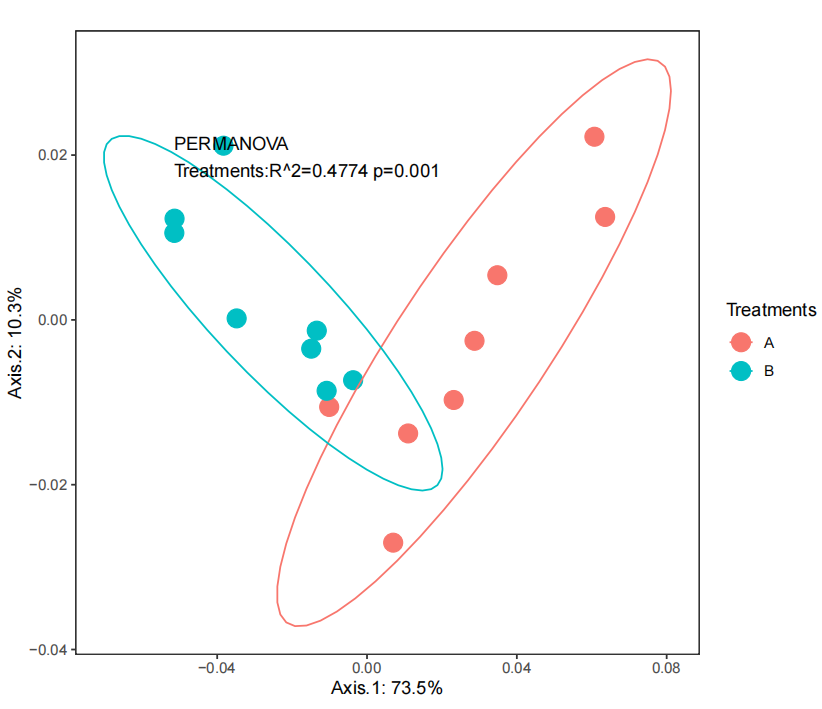
ggplot(jay.pcoa, aes(x=Axis.1, y=Axis.2, colour=Treatments)) +
geom_point(size=5) + stat_ellipse(level = 0.9) +
theme_bw()+theme(panel.grid.major=element_line(colour=NA), panel.background = element_rect(fill = "transparent",colour = NA), plot.background = element_rect(fill = "transparent",colour = NA), panel.grid.minor = element_blank())+
# 把两个轴的贡献度写出来
xlab(paste('Axis.1: ', round(jay.h.pc$values$Relative_eig[1],3)*100, '%', sep = '')) +
ylab(paste('Axis.2: ', round(jay.h.pc$values$Relative_eig[2],3)*100, '%', sep = '')) +
theme(panel.background = element_rect(fill = "transparent",colour = NA),
aspect.ratio = 1) +
# 用annotate把双因素结果写在左上角
annotate(geom = 'text',label = lab, size =4,
x = min(jay.pcoa$Axis.1), y = max(jay.pcoa$Axis.2),
hjust = 0,
vjust =1)
结果展示