1、八进制

逢八进一。用8个计数符号表示，0、1、2、3、4、5、6、7。

2、八进制转二进制 

规则：3位二进制转换1位八进制数。1位八进制数转换3位二进制数。

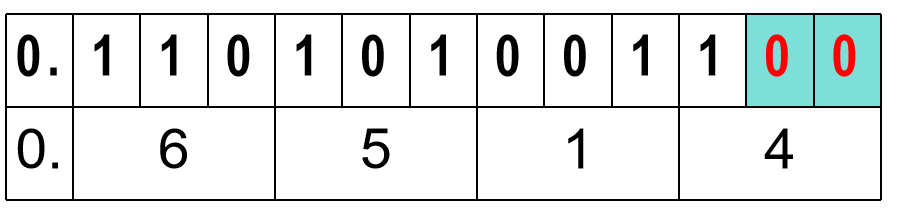
 例如： 10011101B , 0.1101010011B 转换成八进制数。

                         

3、十六进制

用16个计数符号0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F表示数据。

4、十六进制转二进制

1101100010110B转换成十六进制数

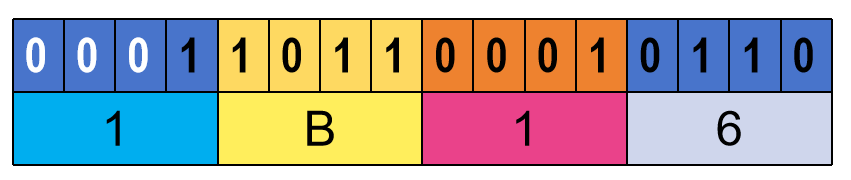
0.110011111101111B转换成十六进制数

问题：计算机只能识别二进制0和1，为什么要有8进制和16进制？有的人会说，是为了增加可读性。但是为啥不用10进制呢。

回答：无论2进制，8进制，16进制，10进制，都是用来给人阅读的，计算机只认高/低电平，不认数字。

由高/低电平可直接转换成2进制数，但2进制数可读性太低。10进制数具有最高的可读性，但由高/低电平转10进制数需要相当复杂的整除和求余运算，效率低。

16进制是2进制和10进制的一个折中，高/低电平可以通过简单的与运算直接转换成16进制数，且其又具有较高的可读性，所以被广泛使用。

 5、整型数表示形式

整型数：用1字节、2字节、4字节整型数等等表示

第1个比特：0表示正数、1表示负数；其余表示数值

正数用原码表示（正数原码、反码、补码相同）

负数的补码：数值转换位二进制数后，各位取反（反码），然后再加1

十进制数327，用2字节整型数表示

十进制-327用2字节整型数表示：

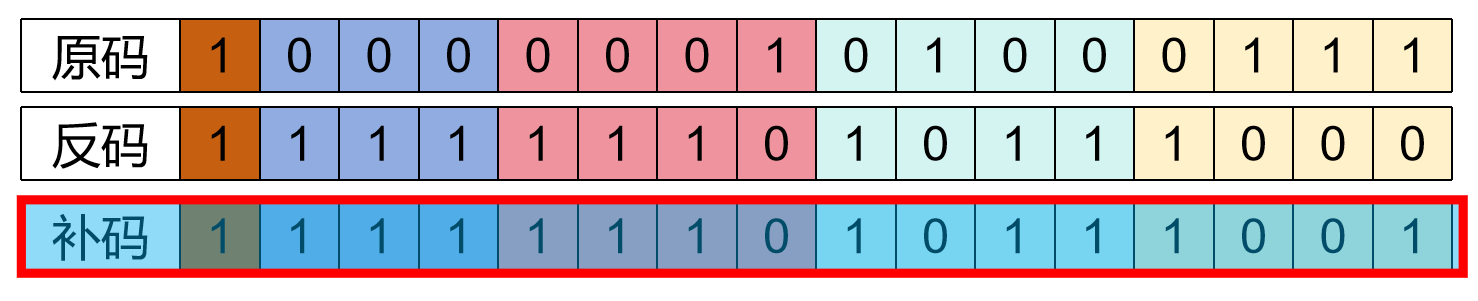
问题：为什么要使用补码表示负数

回答：

1. 可实现符号位与数值位的统一处理。因为负数的补码与正数的原码可以进行相同的运算，这种方式不需要设计复杂的判断符号的电路。
2. 简化了运算符的设计。在使用原码表示负数时，加减法需要分别处理正数和负数，而使用补码表示负数后，加减法只需要一个电路，这大大简化了运算符的设计。
3. 避免了加法溢出。因为二进制算术中的加法可能导致溢出，而使用补码后可以自动忽略溢出的高位，不需要再专门进行处理。

6、浮点数表示形式

浮点数：带有小数的数。一般有4字节（单精度）、8字节（双精度）浮点数。

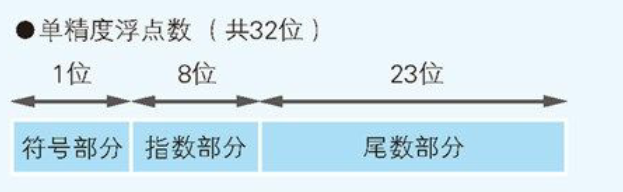
4字节浮点型：32位，1符号位、8位指数位、23位尾数部分

8字节浮点数：64位表示一个浮点数，1bit符号，11bits指数部分，52bits尾数部分。