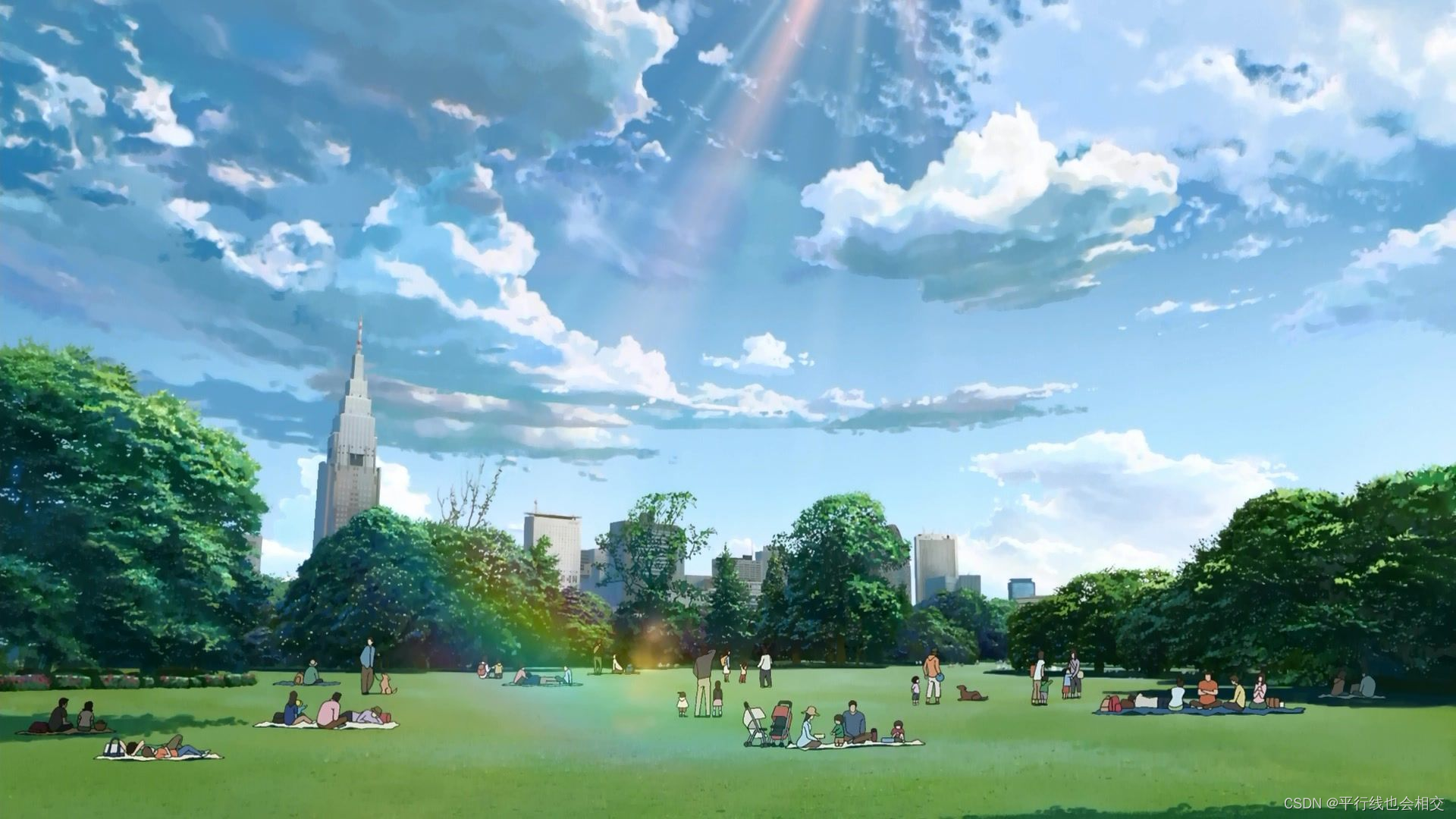个人主页:平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【[PTA刷题训练营]】
目录
- 6-1 简单输出整数
- 6-2 多项式求值(重点掌握)
- 6-3 简单求和
- 6-4 求自定类型元素的平均
- 6-5 求自定类型元素的最大值
- 6-6 求单链表结点的阶乘和
- 6-7 统计某类完全平方数(重点掌握)
- 6-8 简单阶乘计算
- 6-9 统计个位数字
- 6-10 阶乘计算升级版(重点掌握)
- 6-11 求自定类型元素序列的中位数(重点掌握)
- 6-12 判断奇偶性
- 6-13 折半查找
- 总结
- 6-2 多项式求值中多项式的表示方法
- ElementType和ElemType
6-1 简单输出整数
题目链接
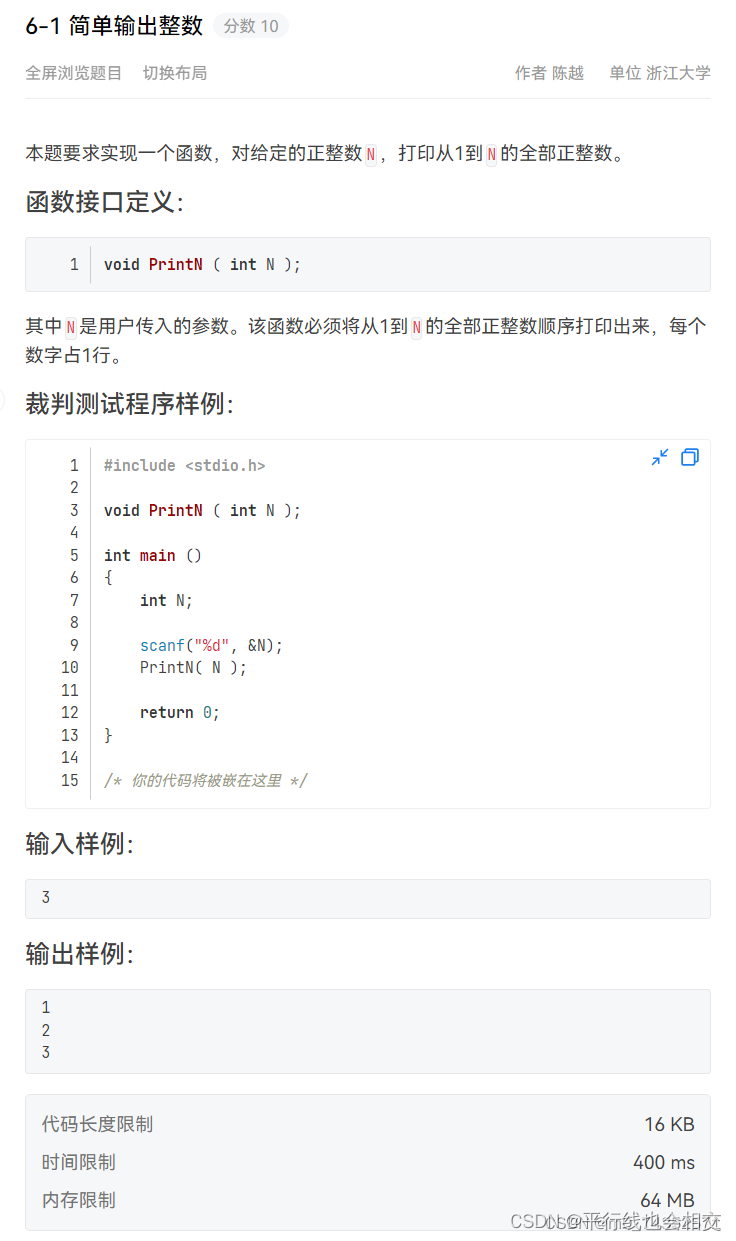
void PrintN(int N)
{
int i=0;
for(i=1;i<=N;i++)
{
printf("%d\n",i);
}
}
6-2 多项式求值(重点掌握)
题目链接
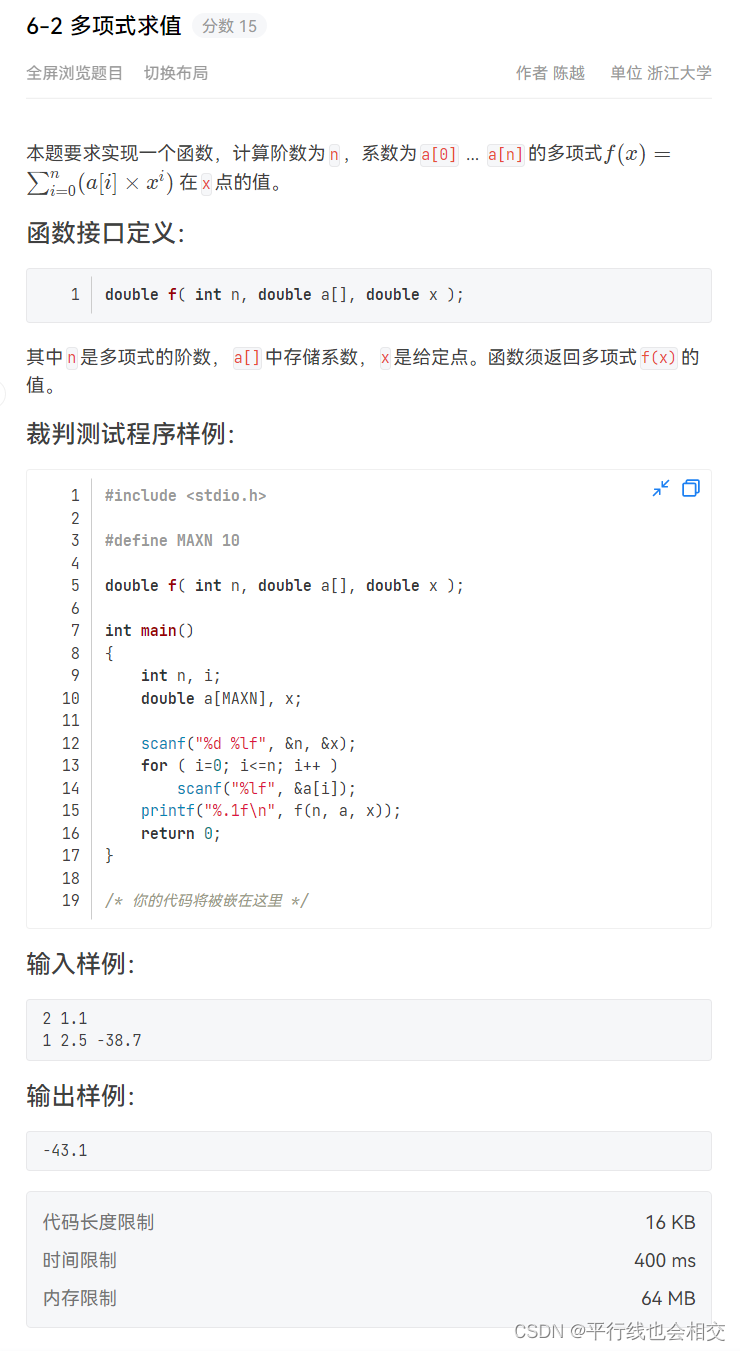
double f( int n, double a[], double x )
{
double sum=0;
double x0=1.0;
int i=0;
for(i=0;i<=n;i++)
{
if(a[i])
{
sum+=x0*a[i];
x0*=x;
}
}
return sum;
}
6-3 简单求和
题目链接
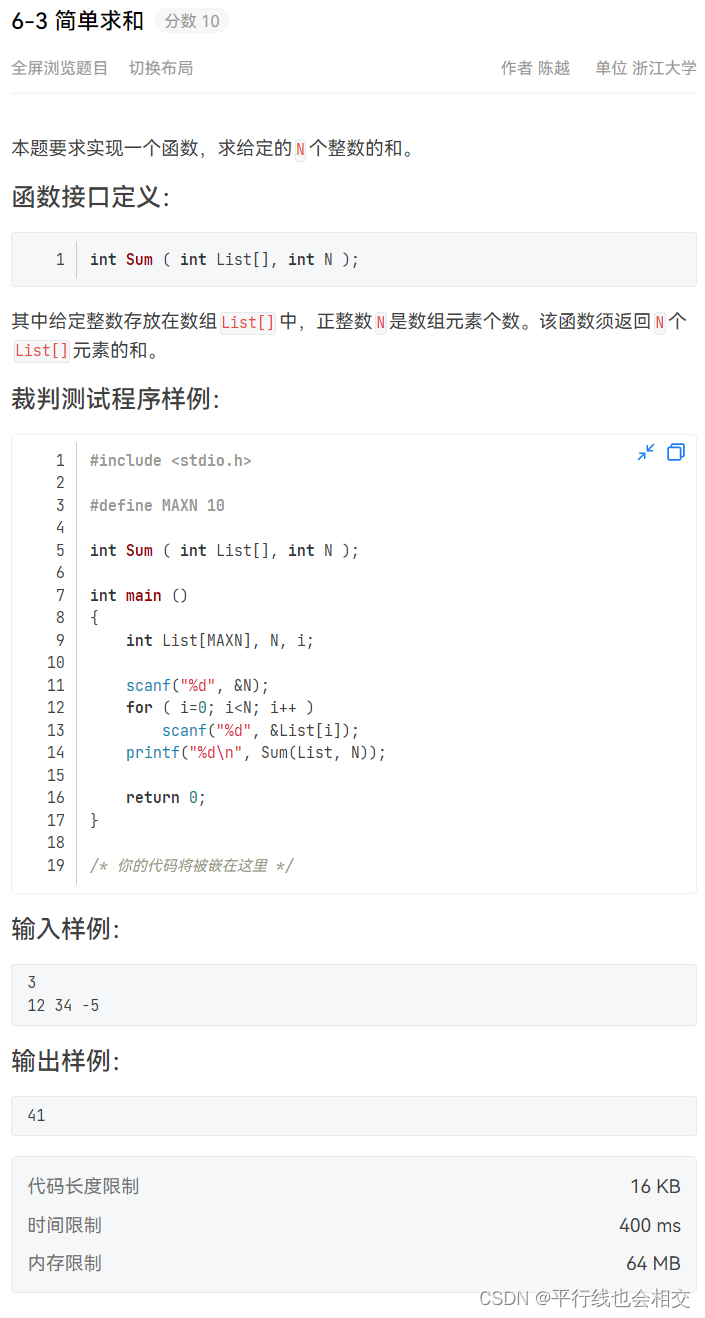
int Sum(int list[],int n)
{
int sum=0;
int i=0;
for(i=0;i<n;i++)
{
sum+=list[i];
}
return sum;
}
6-4 求自定类型元素的平均
题目链接
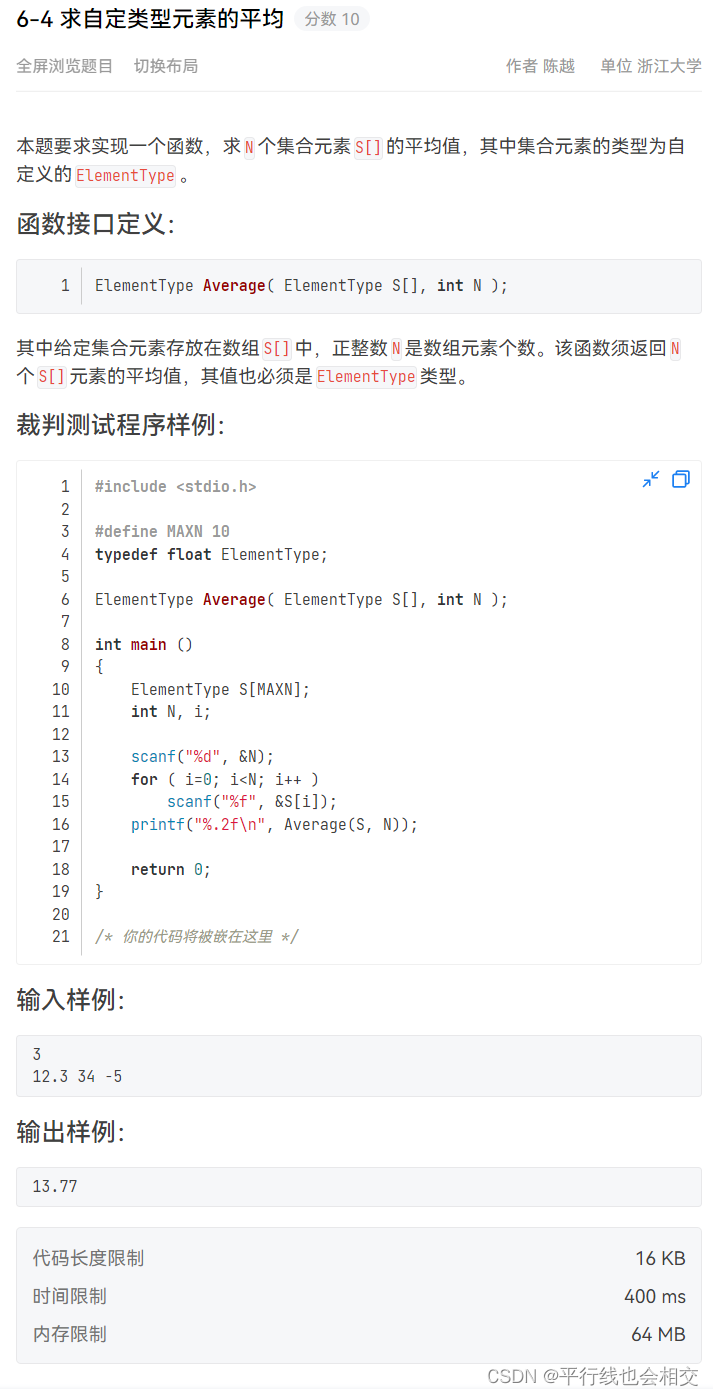
ElementType Average( ElementType S[], int N )
{
ElementType sum=0;
ElementType ave=0;
int i=0;
for(i=0;i<N;i++)
{
sum+=S[i];
}
ave=sum/N;
return ave;
}
6-5 求自定类型元素的最大值
题目链接
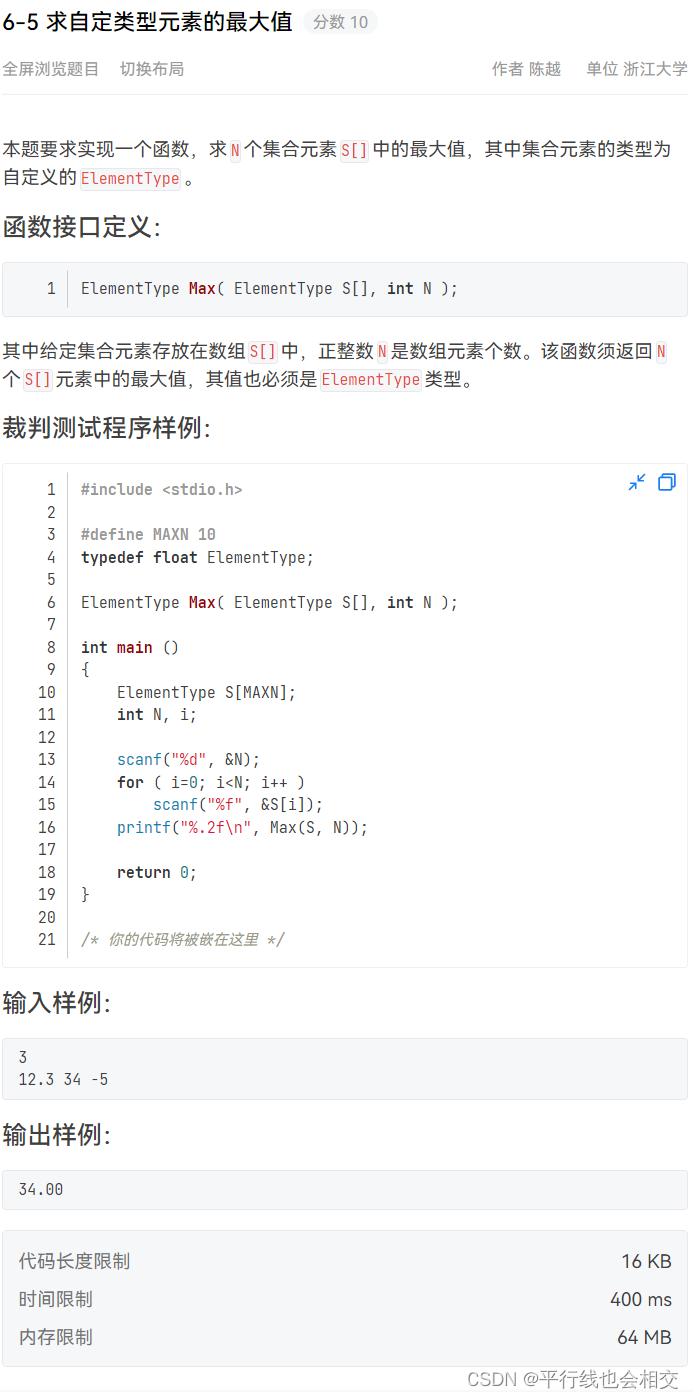
ElementType Max( ElementType S[], int N )
{
ElementType max=S[0];
int i=0;
for(i=1;i<N;i++)
{
if(S[i]>max)
{
max=S[i];
}
}
return max;
}
6-6 求单链表结点的阶乘和
后续补充
6-7 统计某类完全平方数(重点掌握)
题目链接
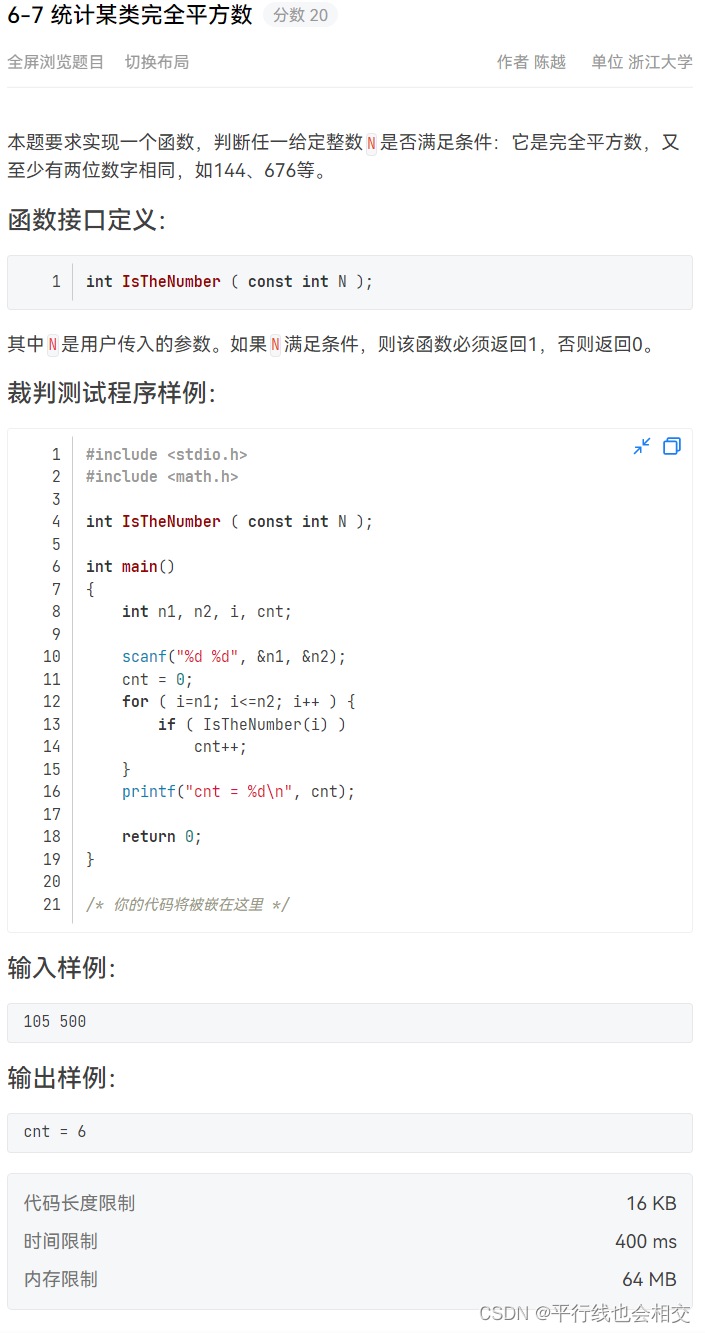
int IsTheNumber ( const int N )
{
int m=(int)(sqrt)(N);
int n=m*m;
if(n==N)
{
int num[10]={0};
int i=0;
while(n)
{
for(i=0;i<=9;i++)
{
if(n%10==i)
{
num[i]+=1;
}
if(num[i]==2)
{
return 1;
}
}
n/=10;
}
}
return 0;
}
6-8 简单阶乘计算
题目链接
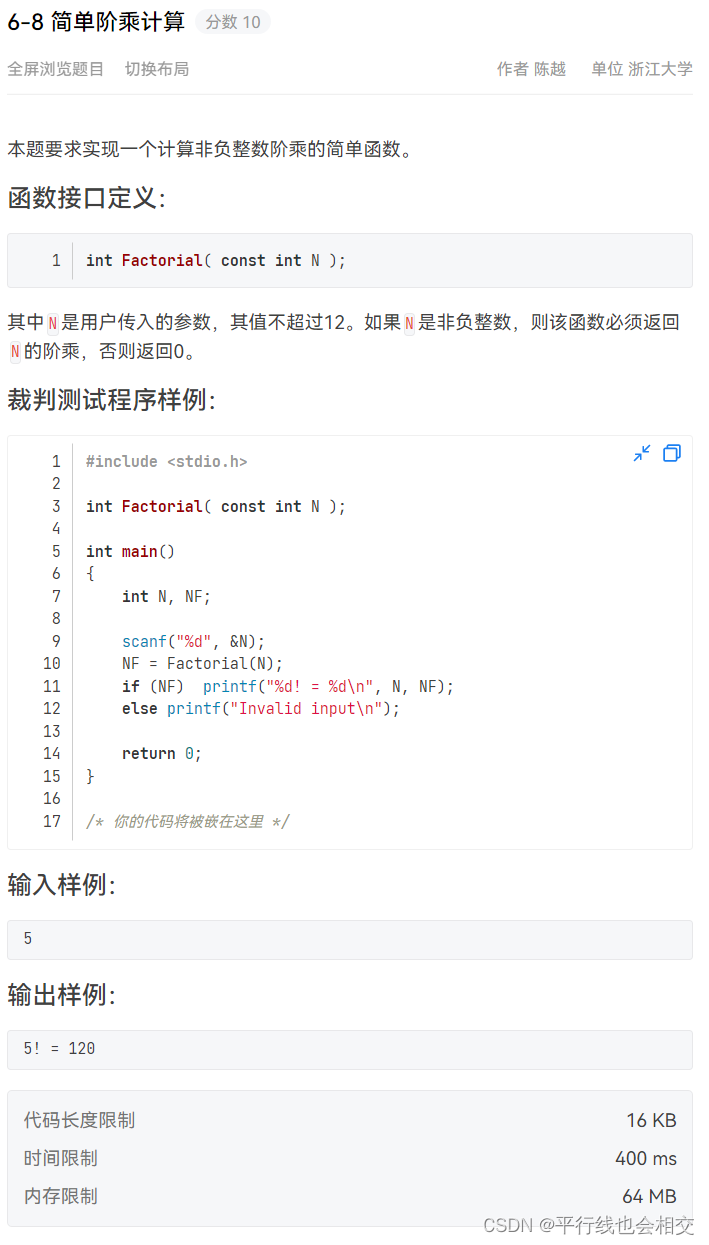
方法一(循环):
int Factorial( const int N )
{
if(N<0)
{
return 0;
}
else if(N==0)
{
return 1;
}
int i=0;
int ret=1;
for(i=1;i<=N;i++)
{
ret*=i;
}
return ret;
}
方法二(递归):
int Factorial( const int N )
{
if(N<0)
{
return 0;
}
else if(N==0)
{
return 1;
}
return N*Factorial(N-1);
}
6-9 统计个位数字
题目链接
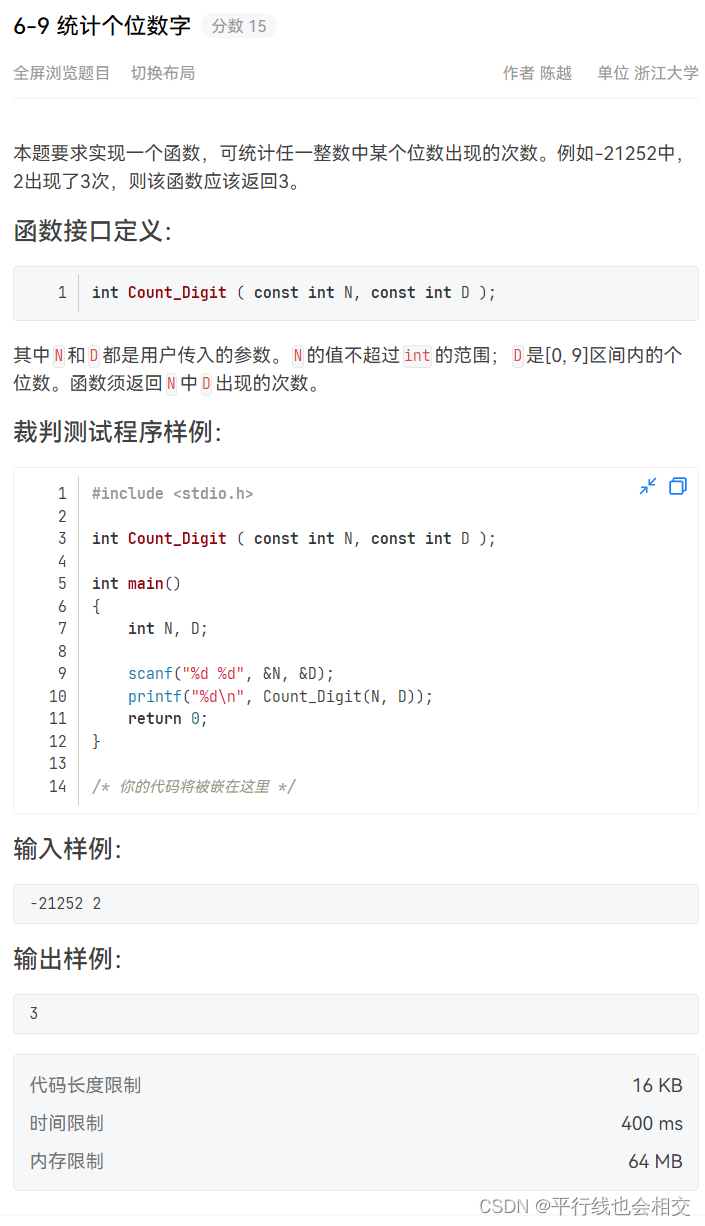
方法一:(此方法是我自己写的,虽然有点混乱,但好在结果正确)
int Count_Digit ( const int N, const int D )
{
if(N==0)
{
return 1;
}
int tmp1=N;
if(tmp1<0)
{
tmp1=-tmp1;
}
int tmp2=tmp1;
int tmp3=tmp1;
int i=0;
int k=0;//k表示为几位数
while(tmp2)
{
k++;
tmp2/=10;
}
int count=0;
for(i=0;i<k;i++)
{
if(tmp3%10==D)
{
count++;
}
tmp3/=10;
}
return count;
}
6-10 阶乘计算升级版(重点掌握)
题目链接
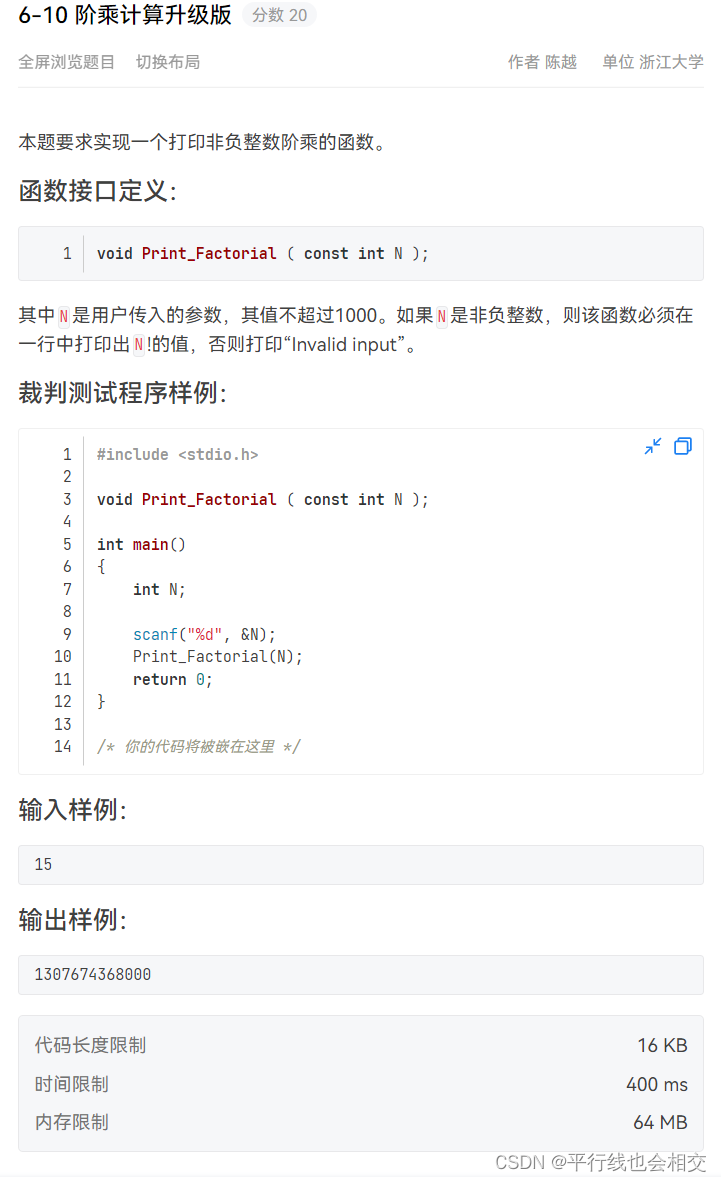
void Print_Factorial(const int N)
{
char a[3000];
int alength = 1;
a[0] = 1;
if (N < 0)
{
printf("Invalid input");
return;
}
int i = 2;
for (i = 2; i <= N; i++)
{
int z = 0;
int k = 0;
for (k = 0; k < alength; k++)
{
int t = i * a[k] + z;
a[k] = t % 10;
z = t / 10;
}
while (z)
{
a[alength++] = z % 10;
z /= 10;
}
}
for (i = alength - 1; i >= 0; i--)
{
printf("%d", a[i]);
}
}
6-11 求自定类型元素序列的中位数(重点掌握)
题目链接
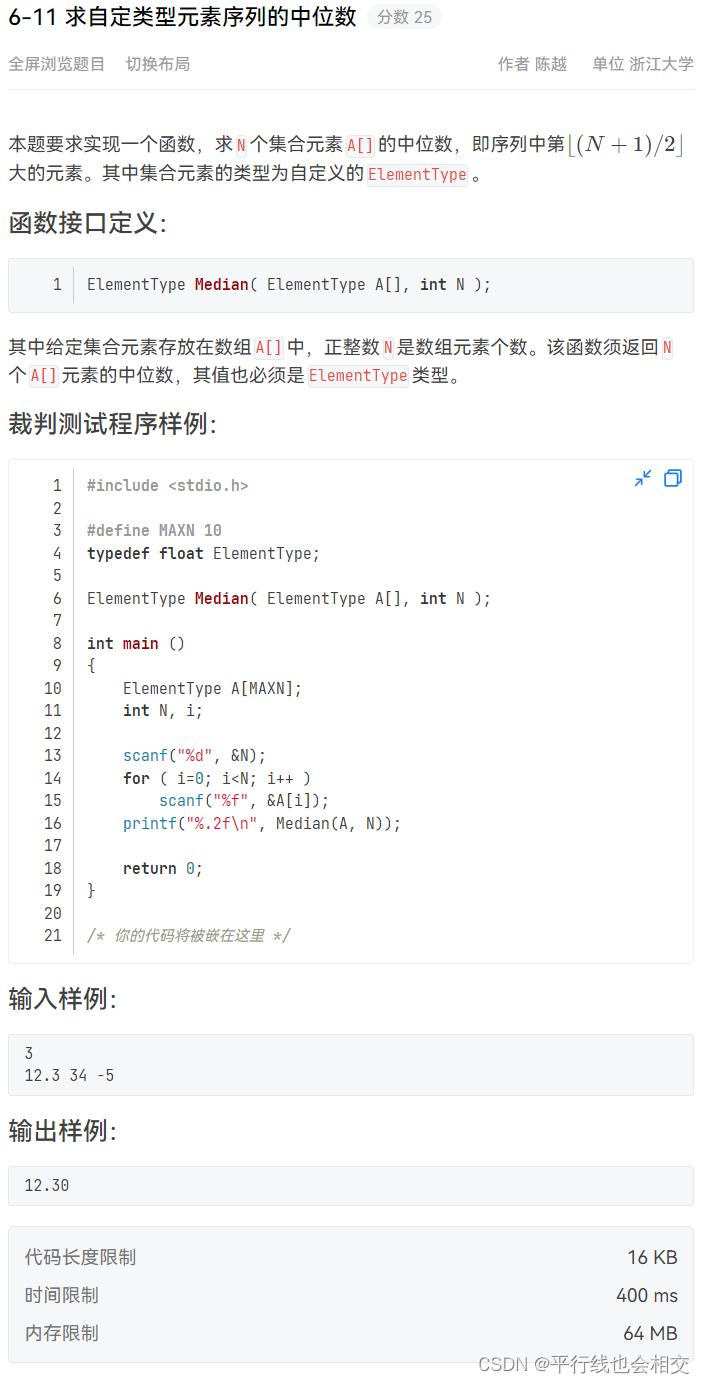
ElementType Median(ElementType A[], int N)
{
ElementType i = 0;
for (i = 0; i < N - 1; i++)
{
int j = 0;
for (j = 0; j < N - 1 - i; j++)
{
if (A[j] > A[j + 1])
{
ElementType tmp = 0;
tmp = A[j];
A[j] = A[j + 1];
A[j + 1] = tmp;
}
}
}
ElementType ret = 0;
if (N % 2 == 0)
{
return ret = A[(N + 1) / 2];
}
else
{
return ret = A[(N + 1) / 2 - 1];
}
}//超时但结果正确
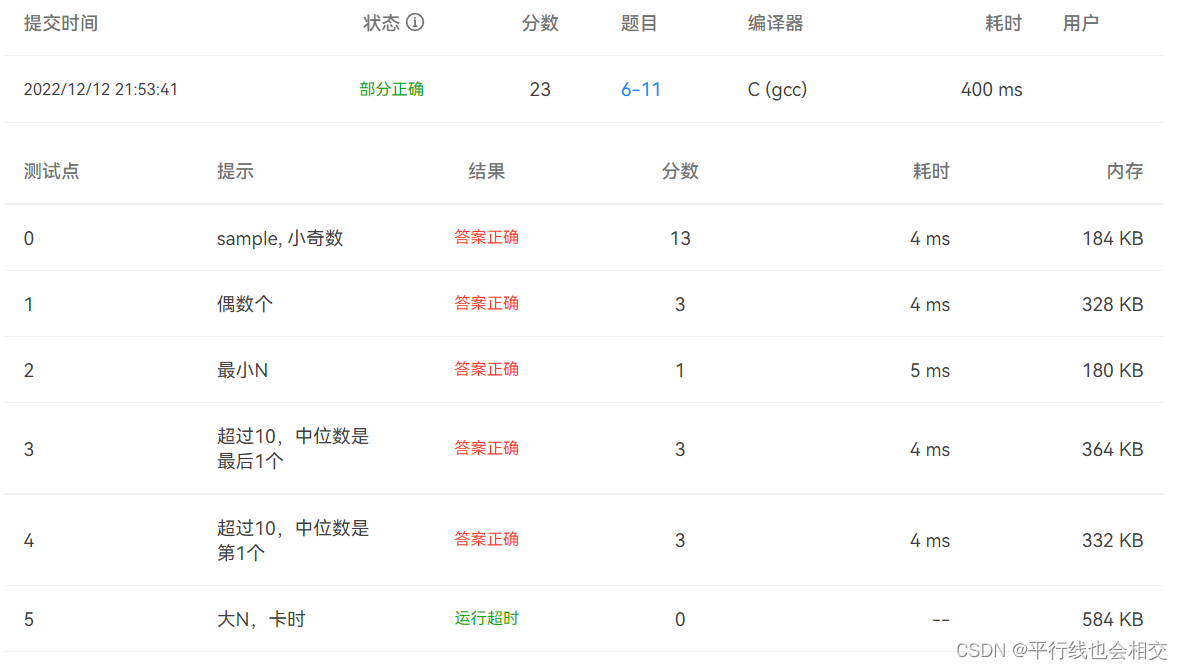
上述代码写的时候结果正确,但是很遗憾超时了😂不过骗点分还是没问题的,哈哈😄。
下面是我找到的另外一种做法:
ElementType Median(ElementType A[], int N)
{
int k = 0;
ElementType tmp = 0;
int i = 0;
for (i = N / 2; i > 0; i = i / 2)
{
int j = 0;
for (j = i; j < N; j++)
{
tmp = A[j];//将找到的中位数放到中间变量中去
for (k = j; k >= i; k = k - i)
{
if (tmp < A[k - i])
{
A[k] = A[k - i];
}
else
{
break;
}
}
A[k] = tmp;
}
}
return A[N / 2];
}
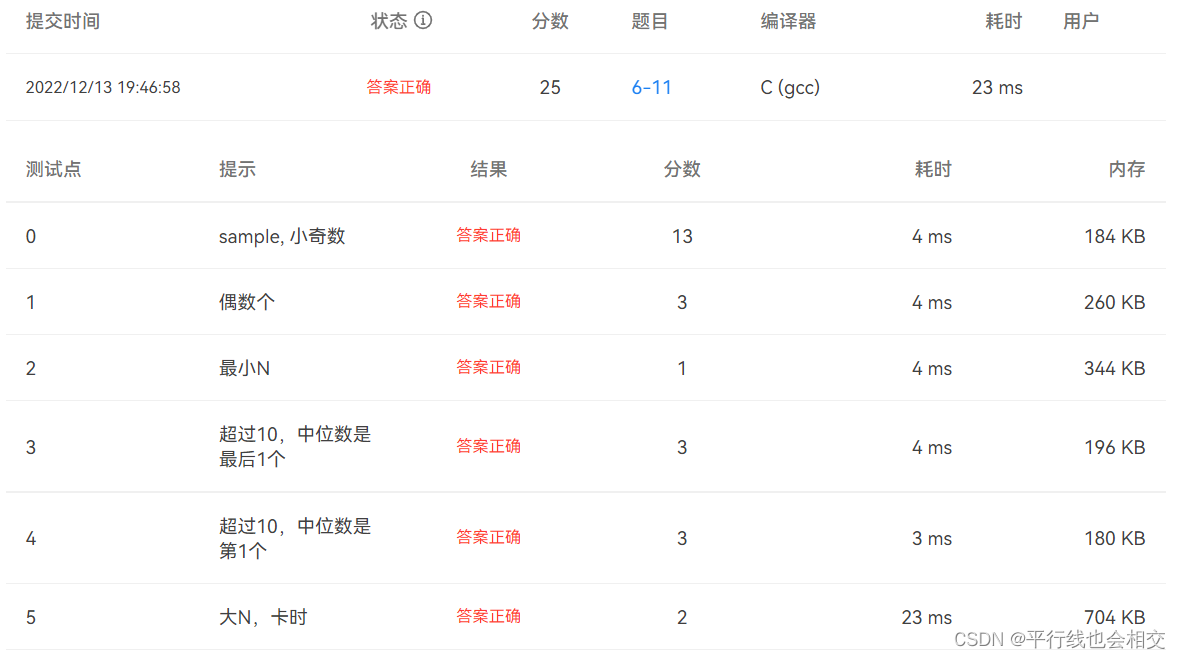
6-12 判断奇偶性
题目链接
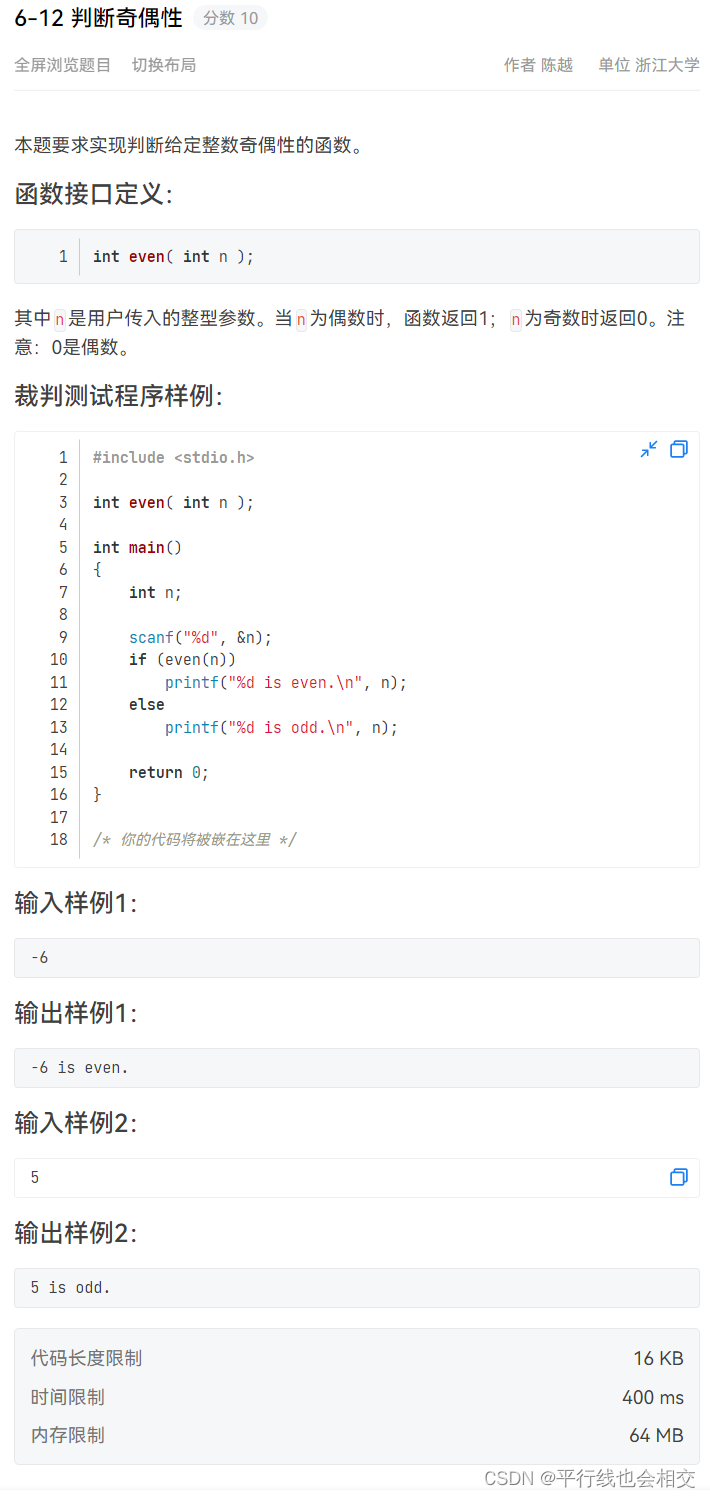
int even( int n )
{
if(n%2==0)
return 1;
return 0;
}
6-13 折半查找
后续补充
总结
6-2 多项式求值中多项式的表示方法
多项式求值中多项式即:

这里我想说的是x的i次方该如何表示,其中让我感到巧妙的是这一部分:x0*=x;。
ElementType和ElemType
Element Type:typedef int ElementType;定义Element Type为int类型
ElemType:#define ElemType int;定义ElemType为int类型
这两个的作用都是一样的,没有区别,只不过定义的方式不同而已:
对于**typedef int ElementType;是重命名
对于#define ElemType int;是宏定义**
由于笔者还没怎么接触到数据结构,所以有些更好的题解不能进行没有写到,后续再给大家补充,另外6-6和6-13也是类似情况,请谅解,我会尽力及时补充。蟹蟹各位。😀