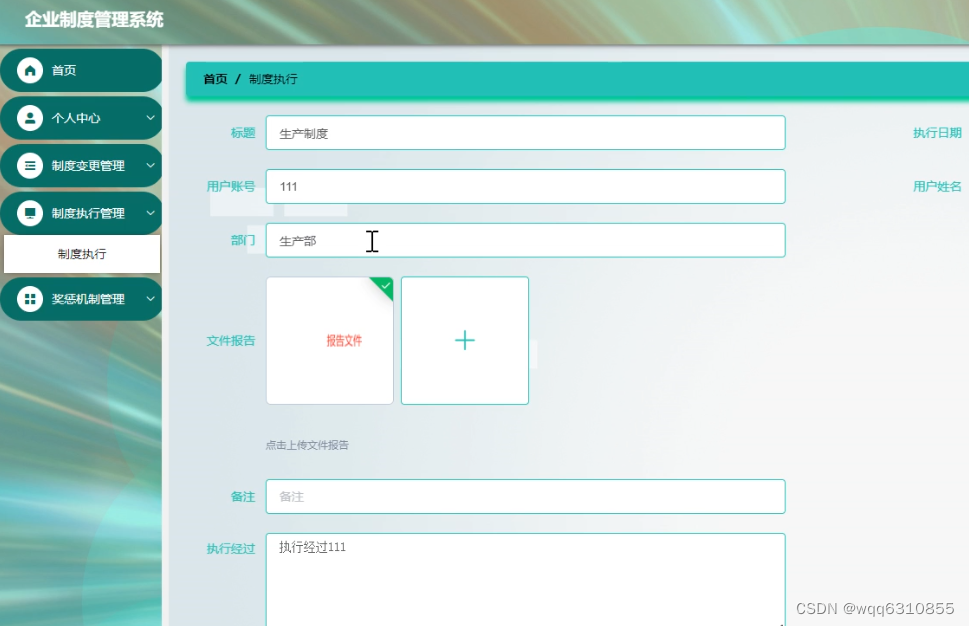
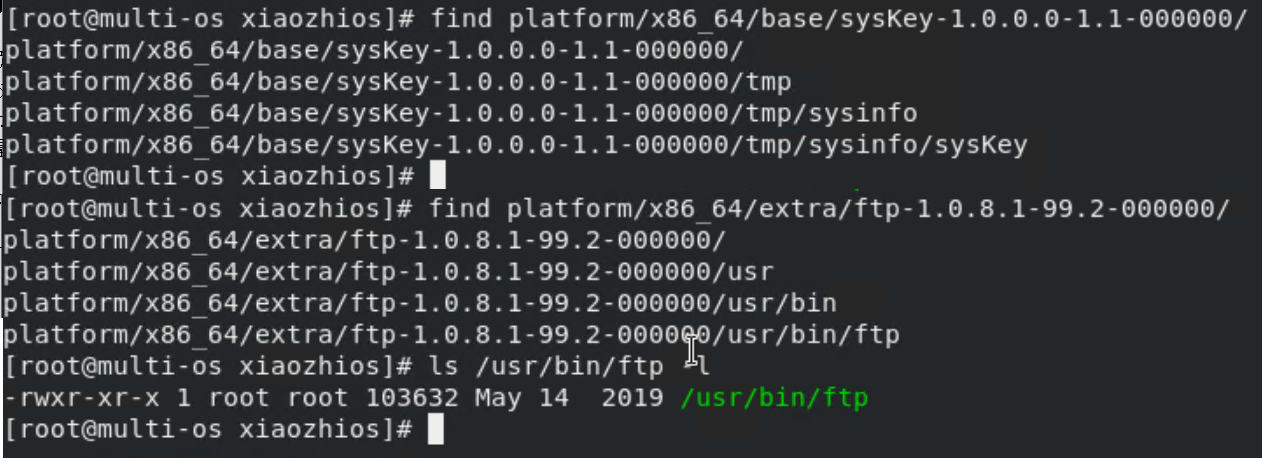
d | a, a | b  ==>  d | ax + by

(a, b) = （b, a mod b）

证明：a mod b = a - [a / b] * b = a - c * b   注：[ ] 为下取整符号，[a / b] 记为c

所以，(a, b) = （b, a - c * b）= （b, a mod b）

以下证明(a, b) = （b, a - c * b）

对于左边任何一个公约数d，d | a, d | b, 由数论基本性质 d | a, a | b  ==>  d | ax + by知，

d| b 且 d | a - c * b，左可推出右（即左边的任何一个公约数都是右边的公约数）

对于右边任何一个公约数d，d | b, d | a - c * b, 由数论基本性质 d | a, a | b  ==>  d | ax + by知，

d | a - c * b + c * b，即 d | a，又因为d | b，所以右可以推出左（即右边的任何一个公约数都是左边的公约数）

所以，两边的公约数集合是相同的，所以左边的最大公约数等于右边的最大公约数

#include <iostream>

using namespace std;

int gcd(int a, int b)
{
    return b ? gcd(b, a % b) : a;
}

int main()
{
    int n;
    scanf("%d", &n);
    
    while (n --)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", gcd(a, b));
    }
    
    return 0;
}

注：(a, 0) = a，a和0的最大公约数是a，因为0可以整除任何数