详解双端队列单调队列

news2024/10/6 10:36:23

1. 双端队列

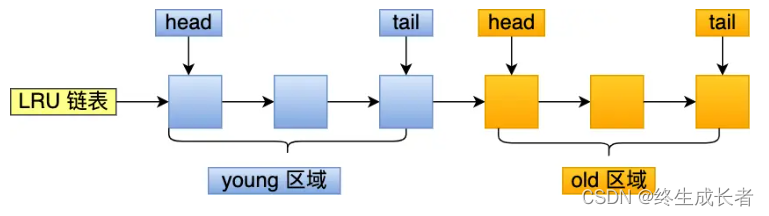
双端队列（Double-ended Queue），简称Deque，是一种具有特殊功能的线性数据结构。它支持从两端进行元素的插入和删除操作，因此可以在队列和栈之间灵活地切换操作。双端队列在编程中经常用于需要在队列和栈之间切换操作的场景，或者需要在任意一端高效地进行插入和删除操作的情况。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-R7ge0a9D-1691652609363)(C:/Users/HUASHUO/AppData/Roaming/Typora/typora-user-images/image-20230810140011519.png)]

双端队列的基本概念包括以下几个方面：

  1. 插入和删除操作：双端队列允许从队列的前端和后端进行插入和删除操作。这意味着你可以在队列的头部和尾部插入元素，也可以从头部和尾部删除元素。

  2. 队列和栈操作：双端队列可以用于模拟队列和栈的操作。当你只从一端插入元素，从另一端删除元素时，它类似于队列。当你从同一端插入和删除元素时，它类似于栈。

  3. 动态调整大小：双端队列可以根据需要动态调整大小，以容纳更多或更少的元素。这可以帮助节省内存并提高性能。

  4. 实现方式：双端队列可以通过数组或链表来实现。数组实现可能需要在插入和删除元素时进行数据的移动，而链表实现则可以更轻松地在任意位置进行插入和删除。

    注：由于双端队列允许从队头和队尾插入和删除数据，因此为了提高插入和删除的效率，当用链表来实现时，应该用双向链表

  5. 常见操作：常见的双端队列操作包括：

    在队列头部插入元素（push_front）

    在队列尾部插入元素（push_back）

    从队列头部删除元素（pop_front）

    从队列尾部删除元素（pop_back）

    获取队列头部元素（front）

    获取队列尾部元素（back）

    判断双端队列是否为空

    获取双端队列中的元素数量

双端队列在编程中经常用于需要高效地在队列两端进行插入和删除操作的问题，如某些算法和数据结构的实现，以及一些具体的应用场景，如滑动窗口问题等。

下面我们用双向链表的方式来实现双端队列

1.1 常见操作

1.1.1 结构的定义

typedef struct DequeNode	//队列的节点
{
    struct DequeNode* next;	//指向下一个
    struct DequeNode* prev;	//指向前一个
    int data;	//数据域
}DQNode;

typedef struct Deque
{
    DQNode* front;	//队头指针
    DQNode* tail;	//队尾指针
}Deque;

1.1.2 初始化

void DequeInit(Deque* pq)   //双端队列初始化
{
    assert(pq);

    pq->front = pq->tail = NULL;
}

1.1.3 判空

bool DequeEmpty(Deque* pq)  //双端队列判空
{
    assert(pq);

    return pq->front == NULL;
}

1.1.3 在尾部插入元素

void DequePush_Back(Deque* pq, int val)
{
    assert(pq);
    
    //新建节点
    DQNode* newNode = (DQNode*)malloc(sizeof(DQNode));
    newNode->data = val;
    newNode->next = NULL;
    newNode->prev = NULL;

    if (DequeEmpty(pq))	//如果队列为空，那么队头指针和队尾指针同时指向newNode
    {
        pq->front = pq->tail = newNode;
    }
    else	//否则在队尾指针后插入
    {
        pq->tail->next = newNode;
        newNode->prev = pq->tail;
        pq->tail = newNode;
    }
}

1.1.4 在头部插入元素

void DequePush_Front(Deque* pq, int val) //队头入队
{
    assert(pq);
    
    //新建节点
    DQNode* newNode = (DQNode*)malloc(sizeof(DQNode));
    newNode->data = val;
    newNode->next = NULL;
    newNode->prev = NULL;

    if (DequeEmpty(pq))	//如果队列为空，那么队头指针和队尾指针同时指向newNode
    {
        pq->front = pq->tail = newNode;
    }
    else	//否则在队头指针前插入
    {
        newNode->next = pq->front;
        pq->front->prev = newNode;
        pq->front = newNode;
    }
}

1.1.5 在头部删除元素

void DequePopFront(Deque* pq)    //队头出队
{
    assert(pq);
    assert(!DequeEmpty(pq));	//队列不能为空

    DQNode* temp = pq->front;	//保存队头元素

    pq->front = pq->front->next;	//队头指针指向下一个
    if (pq->front == NULL)	//如果新的队头为空，那么队尾也要置空
        pq->tail = NULL;
    else	//否则将队头指针的prev成员置空
        pq->front->prev = NULL;

    free(temp);	//释放原头节点的内存
}

1.1.6 在尾部删除元素

void DequePopTail(Deque* pq) //队尾出队
{
    assert(pq);
    assert(!DequeEmpty(pq));	//队列不能为空

    DQNode* temp = pq->tail;	//保存队尾元素

    pq->tail = pq->tail->prev;	//队尾指针指向前一个
    if (pq->tail == NULL)	//如果新的队尾为空，那么就将队头也置空
        pq->front = NULL;
    else	//否则将队尾指针的next成员置空
        pq->tail->next = NULL;

    free(temp);
    return ret;
}

1.1.7 返回队头/队尾元素

int DequeTail(Deque* pq)    //取队尾元素
{
    assert(pq);
    assert(!DequeEmpty(pq));

    return pq->tail->data;
}

int DequeFront(Deque* pq)   //取队头元素
{
    assert(pq);
    assert(!DequeEmpty(pq));

    return pq->front->data;
}

1.1.8 销毁队列

void DequeDestroy(Deque* pq)    //销毁双端队列
{
    while (!DequeEmpty(pq))
    {
        DQNode* temp = pq->front;
        pq->front = pq->front->next;

        free(temp);
    }

    free(pq);
}

1.2 单调队列

单调队列（Monotonic Queue），也称为单调栈（Monotonic Stack），是一种特殊的队列（或栈）数据结构，用于解决一些与元素的单调性相关的问题。它在处理连续元素的最值或者满足一定条件的子序列时非常有用，能够在一定程度上减少问题的时间复杂度。

单调队列的基本概念如下：

  1. 单调性：单调队列主要用于处理具有单调性质的问题，可以是单调非递增或单调非递减。也就是说，队列中的元素要么逐渐增大，要么逐渐减小。

  2. 基本操作：单调队列的主要操作是维护队列内元素的单调性。为了实现这一点，通常需要在队列的某一端插入元素，然后从队列的另一端删除不满足单调性的元素。这使得队列中的元素保持单调有序。

  3. 解决问题：单调队列通常用于解决需要快速获取滑动窗口内的最值、找到连续子数组的最值、或者处理其他与单调性相关的问题。通过单调队列，可以在O(N)的时间复杂度内解决这些问题，而暴力方法通常需要O(N^2)的时间复杂度。

  4. 应用场景：一些典型的应用场景包括：

    • 滑动窗口中的最值问题
    • 连续子数组的最值问题
    • 优先级队列的优化（如在 Dijkstra 算法中的应用）
    • 某些动态规划问题的优化

  5. 实现方式：单调队列可以使用双端队列（Deque）来实现，因为双端队列可以从队头和队尾进行插入和删除操作，适用于维护单调性。插入元素时，可以从队尾插入，并删除队列中小于当前元素的元素；删除元素时，从队头删除。

总之，单调队列是一种优雅而强大的数据结构，它可以在一些特定问题中有效地处理具有单调性质的元素，从而提高算法的效率。

先在我们通过一道具体的例题来对单调队列进行更深入的掌握：

1.2.1 队列的最大值

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3D373Pta-1691652609365)(C:/Users/HUASHUO/AppData/Roaming/Typora/typora-user-images/image-20230810144128615.png)]

需要实现:

//队列结构
typedef struct {

} MaxQueue;

//初始化并返回队列指针
MaxQueue* maxQueueCreate() {

}

//获取当前队列最大值
int maxQueueMax_value(MaxQueue* obj) {

}

//队列尾入队
void maxQueuePush_back(MaxQueue* obj, int value) {

}

//队列头出队
int maxQueuePop_front(MaxQueue* obj) {

}

//销毁队列
void maxQueueFree(MaxQueue* obj) {

}

1.2.1.1 思路

如果我们采用暴力解法，那么每插入或者删除一个元素，找一次最大值的时间复杂度就是O(N)，操作N次那么时间复杂度就是O(N2)，显然效率不高，需要另寻他法。

这里我们就采用单调队列的方式来解决问题。那么具体该如何实现呢？

  1. 基于这个题目，我们有必要认清一点：当一个元素进入队列时，它前面所有比它小的元素都不会对答案产生影响。

    举个例子：

    由于数据是从队头出，因此只要数据1还在队列中，数据2也一定在队列中，故比2小的1便不会对答案产生影响

  2. 因此，我们就需要这样一个单调队列：每次从队尾插入数据val之前，都将小于val的数据从队列中删除，这样队列就只留下了对答案有影响的数据。这就等价于要求这个队列是单调递减的，即每个元素的前面都不会存在比他小的元素。

    举个例子，如果对空队列插入89, 22, 69, 16这四个数据：

    <img src="C:/Users/HUASHUO/AppData/Roaming/Typora/typora-user-images/image-20230810151252590.png" alt="image-20230810151252590" style="zoom:67

  3. 那么我们如何高效地实现单调递减的队列呢？我们知道这个单调队列从队头到队尾数据是递减的，因此队尾元素就是最小元素，所以在插入数据之val前，我们只需要通过循环不断从队尾删除小于val的数据就行。

  4. 需要注意：在维护单调队列时会删除对答案没有影响的元素，但这并不是题目要求需要删除的元素，因此我们还需要一个队列来记录所有插入的数据，从而确定front_pop正确的返回值。同时，如果pop的数据等于最大值，那么也要将保存最大值的队列的队头元素删除（单调队列的队头元素就是最大值）

1.2.1.2 实现代码

typedef struct DequeNode    //双向队列节点
{
    struct DequeNode* next;
    struct DequeNode* prev;
    int val;
}DQNode;

typedef struct Deque    //队头指针，队尾指针
{
    DQNode* front;
    DQNode* tail;
}Deque;

typedef struct {    //Q1用来记录最大值，Q2用来记录所有数据
    Deque* DQ1;
    Deque* DQ2;
} MaxQueue;


MaxQueue* maxQueueCreate() {
    MaxQueue* max = (MaxQueue*)malloc(sizeof(MaxQueue));

    max->DQ1 = (Deque*)malloc(sizeof(Deque));
    max->DQ2 = (Deque*)malloc(sizeof(Deque));

    max->DQ1->tail = max->DQ1->front = NULL;
    max->DQ2->tail = max->DQ2->front = NULL;

    return max;
}

int maxQueueMax_value(MaxQueue* obj) {
    if (obj->DQ1->front == NULL)
        return -1;

    return obj->DQ1->front->val;
}

void maxQueuePush_back(MaxQueue* obj, int value) {
    //先将数据插入存储所有数据的队列
    DQNode* newNode1 = (DQNode*)malloc(sizeof(DQNode));
    newNode1->next = NULL;
    newNode1->prev = NULL;
    newNode1->val = value;

    if (obj->DQ2->front == NULL)
    {
        obj->DQ2->front = obj->DQ2->tail = newNode1;
    }
    else
    {
        obj->DQ2->tail->next = newNode1;
        newNode1->prev = obj->DQ2->tail;
        obj->DQ2->tail = newNode1;
    }

    //如果最大值队列不为空并且最大值队列的队尾元素小于插入的数据
    //通过循环确保队列单调递减
    while (obj->DQ1->front != NULL && obj->DQ1->tail->val < value)
    {
        //那么就将队尾元素出队
        DQNode* temp = obj->DQ1->tail;
        obj->DQ1->tail = obj->DQ1->tail->prev;

        if (obj->DQ1->tail == NULL)
            obj->DQ1->front = NULL;
        else
            obj->DQ1->tail->next = NULL;

        free(temp);
    }
	
    //再将数据存入保存最大值的队列
    DQNode* newNode2 = (DQNode*)malloc(sizeof(DQNode));
    newNode2->next = NULL;
    newNode2->prev = NULL;
    newNode2->val = value;

    if (obj->DQ1->front == NULL)
        obj->DQ1->front = obj->DQ1->tail = newNode2;
    else
    {
        obj->DQ1->tail->next = newNode2;
        newNode2->prev = obj->DQ1->tail;
        obj->DQ1->tail = newNode2;
    }
}

int maxQueuePop_front(MaxQueue* obj) {
    if (obj->DQ2->front == NULL)
        return -1;

    DQNode* temp1 = obj->DQ2->front;	//记录待删除的队头
    int ret = temp1->val;   //记录删除数据
    obj->DQ2->front = obj->DQ2->front->next;

    if (obj->DQ2->front == NULL)
        obj->DQ2->tail = NULL;
    else
        obj->DQ2->front->prev = NULL;

    free(temp1);

    //如果删除的数据等于最大值，就将最大值出队
    if (ret == obj->DQ1->front->val)
    {
        DQNode* temp2 = obj->DQ1->front;
        obj->DQ1->front = obj->DQ1->front->next;

        if (obj->DQ1->front == NULL)
            obj->DQ1->tail = NULL;
        else
            obj->DQ1->front->prev = NULL;

        free(temp2);
    }

    return ret;	//返回删除的值
}

void maxQueueFree(MaxQueue* obj) {
    //通过循环将两个队列的节点释放
    
    while (obj->DQ1->front)
    {
        DQNode* temp = obj->DQ1->front;

        obj->DQ1->front = obj->DQ1->front->next;
        free(temp);
    }
    free(obj->DQ1);

    while (obj->DQ2->front)
    {
        DQNode* temp = obj->DQ2->front;

        obj->DQ2->front = obj->DQ2->front->next;
        free(temp);
    }
    free(obj->DQ2);

    free(obj);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/859948.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL多表连接查询2

MySQL多表连接查询2

目录 1 所有有门派的人员信息 2 列出所有用户&#xff0c;并显示其机构信息 3 列出不入派的人员 4 所有没人入的门派 5 列出所有人员和门派的对照关系 6 列出所有没入派的人员和没人入的门派 7 求各个门派对应的掌门人名称: ​8 求所有当上掌门人的平均年龄: 9 求所…
阅读更多...
6.4 (通俗易懂)可视化详解多通道 多通道输入输出卷积代码实现

6.4 (通俗易懂)可视化详解多通道 多通道输入输出卷积代码实现

以前对多通道和多通道输入输出的卷积操作不理解&#xff0c;今天自己在草稿纸上画图推理了一遍&#xff0c;终于弄懂了。希望能帮助到大家。 多通道可视化 一通道的2x2矩阵 torch.Size([2,2]) 相当于 torch.Size([1,2,2])&#xff0c;是一通道的2x2矩阵 二通道的 2x2矩阵 …
阅读更多...
go-zero 是如何实现令牌桶限流的？

go-zero 是如何实现令牌桶限流的？

原文链接&#xff1a; 上一篇文章介绍了 如何实现计数器限流&#xff1f;主要有两种实现方式&#xff0c;分别是固定窗口和滑动窗口&#xff0c;并且分析了 go-zero 采用固定窗口方式实现的源码。 但是采用固定窗口实现的限流器会有两个问题&#xff1a; 会出现请求量超出限…
阅读更多...
断续模式（DCM）与连续模式（CCM)

断续模式（DCM）与连续模式（CCM)

断续模式&#xff08;DCM&#xff09;与连续模式&#xff08;CCM)是开关电源最常用的两种工作模式。当初级开关管导通前&#xff0c;初级绕组还存在能量&#xff0c;不完全传递到次级&#xff0c;这种情况就叫连续模式。若初级绕组能量完全传递到次级&#xff0c;则为断续模式。…
阅读更多...
Linux与安卓安全对抗

Linux与安卓安全对抗

导读大家都知道安卓是基于Linux内核&#xff0c;而且大家也知道Linux的安全性是公认的&#xff0c;那为什么和Linux有着类似嫡系关系的安卓却一直被人诟病不安全呢&#xff1f;要想说清楚这个问题&#xff0c;我们需要了解一下安卓和Linux到底是什么关系&#xff0c;而且这两个…
阅读更多...
中国信通院高质量数字化转型产品及服务全景图发布，合合信息多项AI产品入选

中国信通院高质量数字化转型产品及服务全景图发布，合合信息多项AI产品入选

随着5G、人工智能、大数据等新一代技术的发展&#xff0c;企业在商业竞争中正面临更多不确定性。中国信通院高度关注企业数字化转型中遇到的痛点&#xff0c;发起“铸基计划-高质量数字化转型行动”&#xff0c;链接企业数字化转型供、需两侧的发展需求&#xff0c;以期推动国家…
阅读更多...
MySQL—缓存

MySQL—缓存

目录标题 为什么要有Buffer Poolbuffer pool有多大buffer pool缓存什么 如何管理Buffer Pool如何管理空闲页如何管理脏页如何提高缓存命中率预读失效buffer pool污染 脏页什么时候会被刷入到磁盘 为什么要有Buffer Pool 虽然说MySQL的数据是存储在磁盘中&#xff0c;但是也不能…
阅读更多...
C++——缺省参数

C++——缺省参数

缺省参数的定义 缺省参数是声明或定义函数时为函数的参数指定一个缺省值。在调用该函数的时候&#xff0c;如果没有指定实参&#xff0c;则采用该形参的缺省值&#xff0c;否则使用指定的实参。 void Func(int a 0) {cout << a << endl; } int main() { Func()…
阅读更多...
【C++学习手札】new和delete看这一篇就够了！

【C++学习手札】new和delete看这一篇就够了！

​ 食用指南&#xff1a;本文在有C基础的情况下食用更佳 &#x1f340;本文前置知识&#xff1a; C类 ♈️今日夜电波&#xff1a; Prover—milet 1:21 ━━━━━━️&#x1f49f;──────── 4:01 …
阅读更多...
OI易问卷协助企业服务好员工，收集员工反馈与信息

OI易问卷协助企业服务好员工，收集员工反馈与信息

OI易问卷——企业问卷调查工具 OI易问卷&#xff0c;是群硕专为企业打造&#xff0c;对内服务员工的调查问卷。 集成于办公联合创新平台&#xff0c;并进一步帮助客户实现与微信或企业微信等其他平台的对接。 可以有效促进员工服务数字化&#xff0c;提高各部门工作效率&…
阅读更多...
mysql的相关指令

mysql的相关指令

mysql的相关指令 DML 数据操作语言DQL数据查询 mysql -uroot -p //启动数据库 show databases; //查看有哪些数据库 use 数据库名; //使用某个数据库 show tables; //查看数据库内有哪些表 exit; //退出mysql的命令环境 create database 数据库名称 charset utf8; //创建数据…
阅读更多...
四项代表厂商，Kyligence 入选 Gartner 数据及人工智能相关领域多项报告

四项代表厂商，Kyligence 入选 Gartner 数据及人工智能相关领域多项报告

近日&#xff0c;全球权威的技术研究与咨询公司 Gartner 发布了《2023 年中国数据、分析及人工智能技术成熟度曲线》、《2023 年分析与商业智能技术成熟度曲线报告》、《2023 年数据管理技术成熟度曲线报告》&#xff0c;Kyligence 分别入选这三项报告的指标平台 Metrics Store…
阅读更多...
【Git】 git push origin master Everything up-to-date报错

【Git】 git push origin master Everything up-to-date报错

hello&#xff0c;我是索奇&#xff0c;可以叫我小奇 git push 出错&#xff1f;显示 Everything up-to-date 那么看看你是否提交了message 下面是提交的简单流程 git add . git commit -m "message" git push origin master 大多数伙伴是没写git commit -m "…
阅读更多...
二维码查分系统制作方法大公开：用这个方法，你也可以快速拥有

二维码查分系统制作方法大公开：用这个方法，你也可以快速拥有

自从“双减”政策颁布以来&#xff0c;学校对成绩的公布变得更加重视。尤其是小学年级&#xff0c;将成绩信息从分数制改为等级制进行发布。同时&#xff0c;成绩公布的方式也有了新的规定&#xff1a;禁止公开公布&#xff0c;不允许为学生成绩进行排名&#xff0c;并需要以特…
阅读更多...
Java课题笔记~ ServletConfig

Java课题笔记~ ServletConfig

概念&#xff1a;代表整个web应用&#xff0c;可以和程序的容器(服务器)来通信 <?xml version"1.0" encoding"UTF-8"?> <web-app xmlns"http://java.sun.com/xml/ns/javaee"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instan…
阅读更多...
突破笔试：力扣129. 求根节点到叶节点数字之和

突破笔试：力扣129. 求根节点到叶节点数字之和

1. 题目链接&#xff1a;129. 求根节点到叶节点数字之和 给你一个二叉树的根节点 root &#xff0c;树中每个节点都存放有一个 0 到 9 之间的数字。每条从根节点到叶节点的路径都代表一个数字&#xff1a;例如&#xff0c;从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 …
阅读更多...
操作系统 -- 进程间通信

操作系统 -- 进程间通信

一、概述 进程经常需要与其他进程通信。例如&#xff0c;在一个shell管道中&#xff0c;第一个进程的输出必须传送给第二个进程&#xff0c;这样沿着管道传递下去。因此在进程之间需要通信&#xff0c;而且最好使用一种结构良好的方式&#xff0c;不要使用中断。在下面几节中&…
阅读更多...
day3 STM32 GPIO口介绍

day3 STM32 GPIO口介绍

GPIO接口简介 通用输入输出接口GPIO是嵌入式系统、单片机开发过程最常用的接口&#xff0c;用户可以通过编程灵活的对接口进行控制&#xff0c;实现对电路板上LED、数码管、按键等常用设备控制驱动&#xff0c;也可以作为串口的数据收发管脚&#xff0c;或AD的接口等复用功能使…
阅读更多...
ElasticSearch：项目实战（2）

ElasticSearch：项目实战（2）

ElasticSearch: 项目实战 (1) 需求&#xff1a; 新增文章审核通过后同步数据到es索引库 1、文章服务中添加消息发送方法 在service层文章新增成功后&#xff0c;将数据通过kafka消息同步发送到搜索服务 Autowiredprivate KafkaTemplate<String,String> kafkaTemplate;/…
阅读更多...
【go语言学习笔记】04 Go 语言工程管理

【go语言学习笔记】04 Go 语言工程管理

文章目录 一、质量保证1. 单元测试1.1 定义1.2 Go 语言的单元测试1.3 单元测试覆盖率 2. 基准测试2.1 定义2.2 Go 语言的基准测试2.3 计时方法2.4 内存统计2.5 并发基准测试2.6 基准测试实战 3. 特别注意 二、性能优化1. 代码规范检查1.1 定义1.2 golangci-lint1.2.1 安装1.2.2…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023