LC-杨辉三角

链接：https://leetcode.cn/problems/pascals-triangle/submissions/

在这里插入图片描述

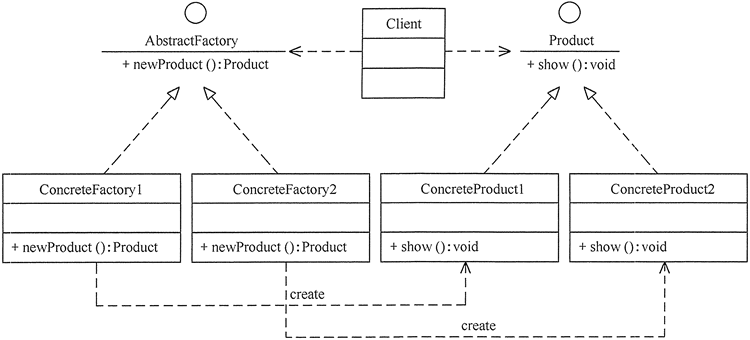
上图就是一个杨辉三角，每个数等于他左上角的数与右上角的数之和。
第一行就是一个1；第二行是两个1；第三行的2就是它肩膀上两个1之和,其余的类似。
所以第n行的数据是根据它上一行的数据计算来的，也就是第n行数据是是由第n-1行数据计算来的。上面的图我们看不出规律，我们可以让数字靠一边，如下：

1  2  3  4  5  6 7

1                       n=1
1  1                    n=2
1  2  1                 n=3
1  3  3  1              n=4
1  4  6  4  1           n=5
1  5  10 10 5  1        n=6
1  6  15 20 15 6  1     n=7

靠一边之后，是一个n行n列的排列，下面我们来看下存在的一些规律。
1.第一行等于1
2.第一列都等于1
3.每行最后一个都是1，也就是第n行第n列是1

最后我们需要找到任意位置的数字是多少的规律，比如我们想要知道第i行第j列的数字是多少。我们看第3行第2列的2是由第2行第1列的1和第2行第2列的1加起来；第5行第3列的6是由第4行的第2列和第4行的第3列3加起来，所以第i行第j列是由第i-1行第j-1列加上第i-1行第j列。

下面我们看下文字转成的代码:

    private int f(int i, int j) {//0 1
        //第一列或者第i行第i列：数字为1
        if (j == 0 || i == j) {
            return 1;
        }
        return f(i - 1, j - 1) + f(i - 1, j);
    }

下面是整个题目的代码：

    public List<List<Integer>> generate(int numRors) {
        List<List<Integer>> a = new ArrayList<List<Integer>>();
        for (int k = 0; k < numRors; k++) {
            List temp = new ArrayList();
            for (int l = 0; l <= k; l++) {
                temp.add(k, l));
            }
            a.add(temp);
        }
        return a;
    }


    private int f(int i, int j) {
        //第一列或者第i行第i列：数字为1
        if (j == 0 || i == j) {
            return 1;
        }
        return f(i - 1, j - 1) + f(i - 1, j);
    }