前言
本期通过几道OJ题,上手用用string。
1. 把字符串转换成整数
描述
将一个字符串转换成一个整数,要求不能使用字符串转换整数的库函数。 数值为 0 或者字符串不是一个合法的数值则返回 0
数据范围:字符串长度满足0 ≤ n ≤100
进阶:空间复杂度 O(1) ,时间复杂度 O(n)
注意:
①字符串中可能出现任意符号,出现除 +/- 以外符号时直接输出 0
②字符串中可能出现 +/- 且仅可能出现在字符串首位。
输入描述:
输入一个字符串,包括数字字母符号,可以为空
返回值描述:
如果是合法的数值表达则返回该数字,否则返回0
示例1
输入:
"+2147483647"
返回值:
2147483647
示例2
输入:
"1a33"
返回值:
0
思路+算法
遍历,判断每次遍历到的元素
- 是’+':跳过
- 是’-':保存标记
- 是数字字符:加进 int的sum
- 其他(非法):返回0
实现
class Solution {
public:
int StrToInt(string str)
{
int flag = 1;
long long ret = 0;
for(size_t i = 0; i < str.size(); ++i)
{
if(str[i] == '+')
continue;
else if(str[i] == '-')
flag = -1;
else if(str[i] >= '0' && str[i] <= '9')
ret = ret * 10 + (str[i]-'0');
else
return 0;
}
return flag * ret;
}
};
2.字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = "11", num2 = "123"
输出:"134"
示例 2:
输入:num1 = "456", num2 = "77"
输出:"533"
提示:
1 <= num1.length, num2.length <= 104num1和num2都只包含数字0-9num1和num2都不包含任何前导零
思路和算法
直接模拟竖式加法:和的某一位 = 两数某一位的和 + 先前留下的进位。
竖式加法从后往前加即可。
实现
class Solution {
public:
//和的当前位 = 两数当前位的和 + 进位
string addStrings(string num1, string num2)
{
string ret;
int n = num1.size() > num2.size() ? num1.size() : num2.size();
ret.reserve(n+1); //最大的两个n位数相加也只可能是n+1位数
int i = num1.size() - 1, j = num2.size() - 1, add = 0;
while(i >= 0 || j >= 0 || add != 0)
{
//用int相加
int x = i >= 0 ? num1[i]-'0' : 0;
int y = j >= 0 ? num2[j]-'0' : 0;
int sum = x + y + add;
//保存char
ret.push_back((sum % 10) + '0');
//保存进位
add = sum / 10;
--i;
--j;
}
reverse(ret.begin(), ret.end());
return ret;
}
};
- reserve提前开好空间,避免频繁扩容
- 同时遍历两个容器,可以用逻辑或来一口气弄完(逻辑要自洽)。
3. 反转字符串中的单词 III
给定一个字符串 s ,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。
示例 1:
输入:s = "Let's take LeetCode contest"
输出:"s'teL ekat edoCteeL tsetnoc"
示例 2:
输入: s = "God Ding"
输出:"doG gniD"
提示:
1 <= s.length <= 5 * 104s包含可打印的 ASCII 字符。s不包含任何开头或结尾空格。s里 至少 有一个词。s中的所有单词都用一个空格隔开。
思路和算法
遍历s,找空格前保存当前位置start ==> 找空格位置i ==> 交换区间[start, i]中的数据 ==> 跳过空格
实现
class Solution {
public:
//遍历找空格并记录区间,找到空格就交换区间内数据
string reverseWords(string s)
{
int len = s.size();
int i = 0;
while(i < len)
{
int start = i;
//找空格
while(i < len && s[i] != ' ') ++i;
//交换
int left = start, right = i - 1;
while(left < right) swap(s[left++], s[right--]);
//跳过空格
while(i < len && s[i] == ' ') ++i;
}
return s;
}
};
4. 字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
**注意:**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。
示例 1:
输入: num1 = "2", num2 = "3"
输出: "6"
示例 2:
输入: num1 = "123", num2 = "456"
输出: "56088"
提示:
1 <= num1.length, num2.length <= 200num1和num2只能由数字组成。num1和num2都不包含任何前导零,除了数字0本身。
思路和算法
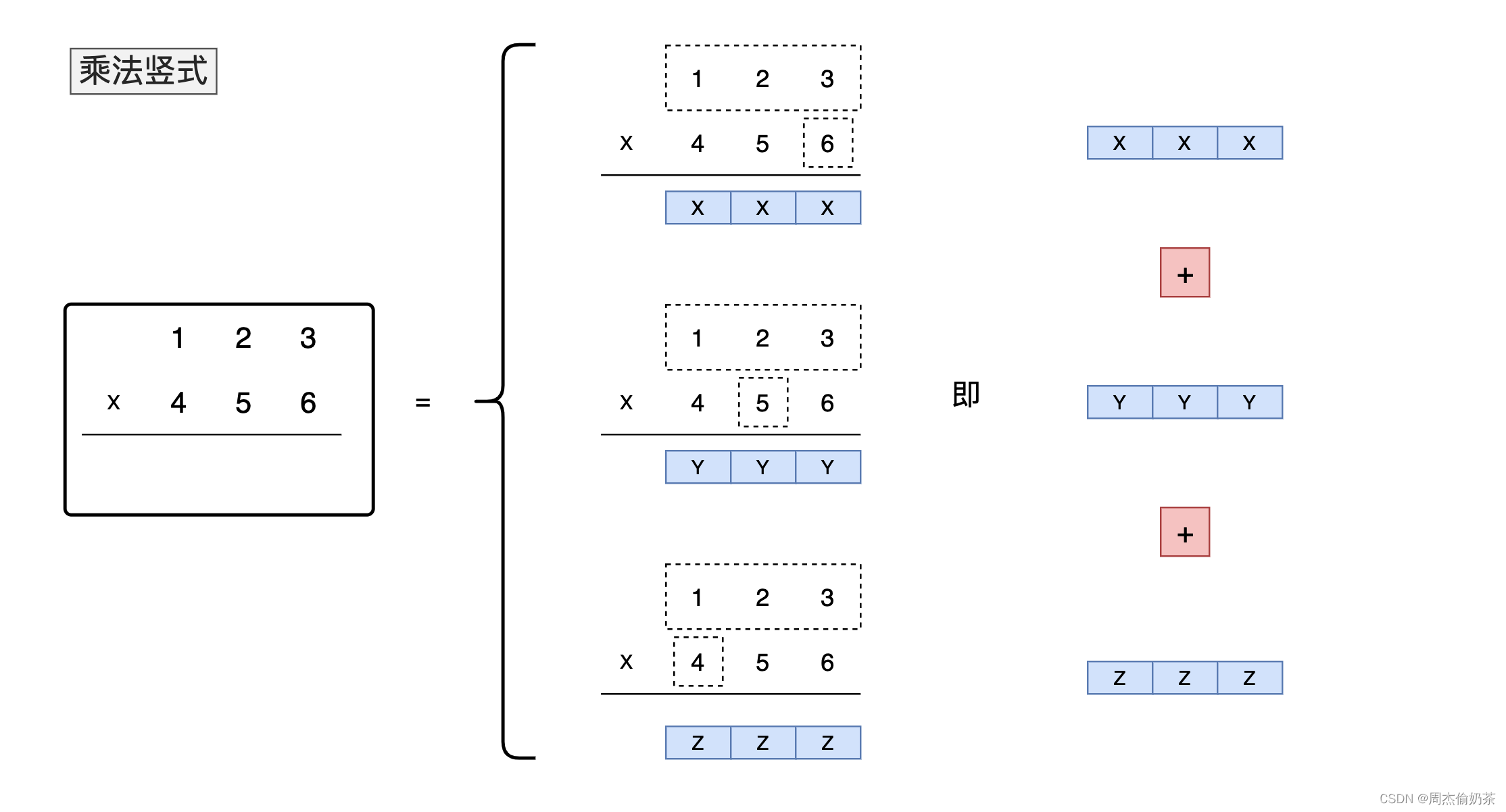
123 * 6 = 3*6 + 2*6 + 1*6
123 * 5 = 3*5 + 2*5 + 1*5
123 * 4 = 3*4 + 2*4 + 1*4
思路仍然是模拟竖式,不过这次是 两数的各个位都从后向前乘,再将乘积相加(可以把字符串相加拿过来用一下)。
实现
class Solution {
public:
//模拟竖式计算
string multiply(string num1, string num2)
{
if(num1 == "0" || num2 == "0")
return "0";
//123 * 456 =
//123 * 4
//123 * 5
//123 * 6
string ans = "0";
//整形计算
int n1 = num1.size(), n2 = num2.size();
//i 拿 6 5 4
for(int i = n2 - 1; i >= 0; --i)
{
string cur; //保存一次乘积,如123 * 4
int add = 0; //保存进位
for(int j = n2 - 1; j > i; --j) cur.push_back(0); //补0
//123 * 4
//123 * 5
//123 * 6
//j 拿 1 2 3
int y = num2[i] - '0';
for(int j = n1 - 1; j >= 0; --j)
{
//3 * 4
//3 * 5
//3 * 6
int x = num1[j] - '0';
int product = x * y + add;
cur.push_back(product % 10);
add = product / 10;
}
//加上进位
while(add)
{
cur.push_back(add % 10);
add /= 10;
}
reverse(cur.begin(), cur.end());
//保存字符
for(auto& e : cur) e += '0';
ans = addStrings(ans, cur);
}
return ans;
}
string addStrings(string num1, string num2)
{
string ret;
int n = num1.size() > num2.size() ? num1.size() : num2.size();
ret.reserve(n+1); //最大的两个n位数相加也只可能是n+1位数
int i = num1.size() - 1, j = num2.size() - 1, add = 0;
while(i >= 0 || j >= 0 || add != 0)
{
//用int相加
int x = i >= 0 ? num1[i]-'0' : 0;
int y = j >= 0 ? num2[j]-'0' : 0;
int sum = x + y + add;
//保存char
ret.push_back((sum % 10) + '0');
//保存进位
add = sum / 10;
--i;
--j;
}
reverse(ret.begin(), ret.end());
return ret;
}
};
今天的分享就到这里了,感谢观看!
这里是培根的blog,期待与你共同进步,
下期见~




![新兴新能源设施[1]--盐穴压缩空气储能相关配套设施](https://img-blog.csdnimg.cn/43b3bf44cf064095a74616ae0bf7ed5a.png)