编程中的宝藏：二分查找

news2024/11/26 12:43:57

二分查找

假设你需要在电话簿中找到一个以字母 “K” 开头的名字（虽然现在谁还在用电话簿呢！）。你可以从头开始翻页，直到进入以 “K” 打头的部分。然而，更明智的方法是从中间开始，因为你知道以 “K” 打头的名字很可能在电话簿的中间部分。

类似地，当你要在字典中查找一个以字母 “O” 开头的单词时，你也会从中间附近开始搜索。

再举一个例子，当你登录 Facebook 时，系统需要核实你是否有该网站的账户。它必须在数据库中查找你的用户名。如果你的用户名是 “karlmageddon”，Facebook 可以从以字母 “A” 开头的部分开始查找。然而，更聪明的做法是从中间开始查找。

这些场景都涉及到查找问题，而在所有这些情况下，都可以使用同一种算法来解决，那就是二分查找。

二分查找是一种算法，它的输入是一个有序元素列表（必须有序的原因稍后解释）。如果要查找的元素包含在列表中，二分查找会返回其位置；否则返回 -1。

下面的示例演示了二分查找的工作原理。我们随意选择一个在 1 到 100 之间的数字。

Binary Search Example

你的目标是以最少的猜测次数猜到这个数字。每次猜测后，我会告诉你是小了、大了还是猜对了。如果你从 1 开始顺序猜测，过程可能是这样的：

猜测 1 -> 小了
猜测 2 -> 小了
猜测 3 -> 小了
…

这种方法被称为简单查找，更确切地说是傻找。每次猜测只能排除一个数字。如果数字是 99，你最多需要猜测 99 次才能猜对。

更聪明的查找方法

下面是一种更聪明的猜测方法：从 50 开始。

猜测 50 -> 小了，但排除了一半的数字！现在你知道 1 到 50 都是小了。接下来，你猜 75。
猜测 75 -> 大了，又排除了一半的数字！使用二分查找，你猜测的是中间的数字，从而每次都可以排除一半的数字。然后，你猜测 63（50 和 75 之间的数字）。

这就是二分查找，你刚刚学会了一种全新的算法！每次猜测都会排除一半的数字，如下图所示：

Binary Search Steps

不论我心里想的是哪个数字，你最多需要 7 次猜测就能找到，因为每次猜测都会排除很多数字。对比一下：

简单查找：100 步
二分查找：7 步

也许在使用者的角度看，这 97 步的差距似乎微不足道。然而，随着元素数量的增加，二分查找的优势会越来越明显。

现在，让我们考虑一个问题：如果你要在包含 240,000 个单词的字典中查找一个单词，最多需要多少步？假设要查找的单词位于字典的末尾，使用简单查找将需要 240,000 步。而如果使用二分查找，每次都会排除一半的单词，直到最后只剩下一个单词。

在进行二分查找时，每次排除的单词数量是通过将搜索范围减半来计算的。因为字典中有 240,000 个单词，每次排除一半，我们可以计算出每次排除的单词数量，如下：

初始范围：240,000 个单词
第 1 次排除：120,000 个单词
第 2 次排除：60,000 个单词
…（后续步骤省略）

因此，使用二分查找，最多需要 18 次排除就能找到一个特定单词，即使在包含 240,000 个单词的字典中。这是因为每一次排除一半的单词，使得搜索范围迅速减小，直到只剩下一个单词。

仅当列表是有序的时候，二分查找才适用。例如，电话簿中的名字按字母顺序排列，因此可以使用二分查找来查找名字。

运行时间

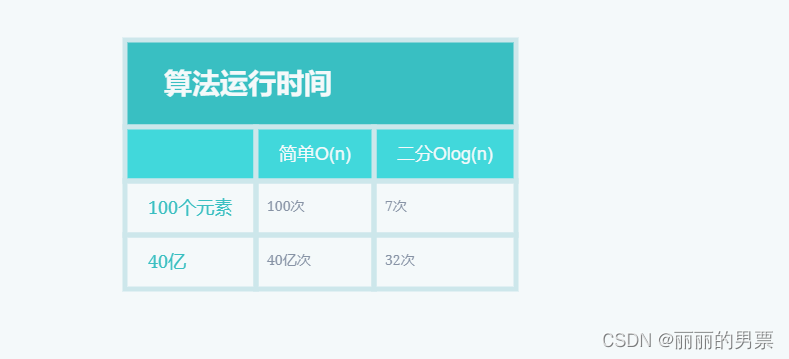
让我们再次回到二分查找。使用二分查找相比于简单查找能节省多少时间呢？简单查找是逐个地检查数字，如果列表包含 100 个数字，最多需要猜测 100 次。而如果列表包含 40 亿个数字，最多需要猜测 40 亿次。换句话说，最多需要的猜测次数与列表的长度相同，这种情况被称为线性时间（linear time）。

然而，二分查找则不同。如果列表包含 100 个元素，最多只需猜测 7 次；如果列表包含 40 亿个数字，最多只需猜测 32 次。相比之下，二分查找的运行时间是对数时间（logarithmic time）。

下表总结了我们所发现的情况：

Comparison

总结

当我们进一步探讨二分查找和简单查找之间的差异时，不难发现，二分查找的性能优势随着元素数量的增加变得更加显著。虽然在开始时，二分查找的速度提升可能并不明显，但随着列表规模的增长，它的优越性将愈发凸显出来。

简单查找以线性时间的方式进行，每增加一个元素，它需要的额外时间也会线性增长。这就导致当元素数量庞大时，每次查找都会变得耗时且不实际。例如，如果你有一个拥有数百万个元素的数据集，使用简单查找进行查询可能会变得极其缓慢，甚至不切实际。然而，二分查找以对数时间的方式运作，每次查找只需要排除一半的元素。

这意味着，尽管数据量增加，每次查找所需的额外时间增长得非常缓慢。就像是在探索一个迷宫时，你只需每次选择一个正确的路径，逐渐逼近目标，而不是逐一检查所有可能的路径。

这种对数级别的优越性意味着，在大数据集或者长列表中，二分查找的速度几乎不会受到影响。它的查询速度可以在常数时间内保持，无论数据规模如何增长。而这也是为什么在现代计算机科学中，二分查找是一种备受推崇的高效算法。

因此，无论是在简单的名字查找、大规模数据处理，还是搜索庞大的字典中的单词，二分查找都是一种强大的工具，能够在海量信息中快速找到目标。在信息爆炸的今天，掌握并充分利用这种高效的算法，对于优化搜索效率、提升数据处理速度至关重要。

代码示例

Python

def binary_search(lst, item):
    left = 0
    right = len(lst) - 1
    while left <= right:
        # 你每次都检查中间的元素。
        mid = (left + right) // 2
        val = lst[mid]
        if val == item:
            return mid
        if val > item:
            # 如果猜的数字大了，就修改right
            right = mid - 1
        else:
            # 如果猜的数字小了，就相应地修改left。
            left = mid + 1
    return -1  # Return -1 if item is not found

my_list = [1, 2, 3, 4, 5, 6, 7, 8]

print(binary_search(my_list, 6))

Java

public class BinarySearch {
    public static int binarySearch(int[] arr, int target) {
        int left = 0;
        int right = arr.length - 1;
        while (left <= right) {
            int mid = (left + right) / 2;
            int val = arr[mid];
            if (val == target) {
                return mid;
            }
            if (val > target) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
        return -1;
    }

    public static void main(String[] args) {
        int[] myArray = {1, 2, 3, 4, 5, 6, 7, 8};
        int searchItem = 6;
        int result = binarySearch(myArray, searchItem);
        System.out.println(result);
    }
}