本文只是对于初学者的一种直观普及，以及对于规划路径可视化的另外一种体会。对于做规划控制的工程师来说太简单。只是本人初学者，在学习控制模块时候对于模块输入参数有所迷惑。所以记录一下。

    首先明确轨迹表达的方式，以及对于控制模块输入的轨迹表达方式：

message ADCTrajectory
{
    .......
    repeated apollo.common.TrajectoryPoint trajectory_point;
    repeated apollo.common.PathPoint path_point;
    .......
}

message TrajectoryPoint
{
    // path point
    optional PathPoint path_point = 1；
    // linear velocity
    optional double v = 2;  // in [m/s]
    // linear acceleration
    optional double a = 3;
    // relative time from beginning of the trajectory
    optional double relative_time = 4;
    // longitudinal jerk
    optional double da = 5;
    // The angle between vehicle front wheel and vehicle longitudinal axis
    optional double steer = 6;
}
message PathPoint
{
    // coordinates
    optional double x = 1;
    optional double y = 2;
    optional double z = 3;

    // direction on the x-y plane
    optional double theta = 4;
    // curvature on the x-y planning
    optional double kappa = 5;
    // accumulated distance from beginning of the path
    optional double s = 6;
    // derivative of kappa w.r.t s.
    optional double dkappa = 7;
    // derivative of derivative of kappa w.r.t s.
    optional double ddkappa = 8;
    // The lane ID where the path point is on
    optional string lane_id = 9;
    // derivative of x and y w.r.t parametric parameter t in CosThetareferenceline
    optional double x_derivative = 10;
    optional double y_derivative = 11;
}

    可以看到ADCTrajectory表示一次规划的结果，其中的repeated字段表示数组。有多个轨迹点和路径点组成一段规划的路径。

1，这里有个理解的误区：ADCTrajectory也可以用来表示参考线，也可以用来表示EGO的实际运行路径。

2，TrajectoryPoint中既有Frenet坐标系下的参数：方位角以及曲率也有实际的笛卡尔坐标系下的位置。以上所有信息都来自上游的规划模块。

3，这些轨迹点中包含该点的速度加速度以及在该点的距离信息。这个距离后面会分析。

    有了以上信息后，发现控制模块的很多参数是已知的，比如速度，距离等信息。所有后端的控制模块的逻辑只需要更具这些轨迹中的要求去执行。至于规划的路径中各个点的速度，距离，方位角信息就是规划模块计算处理的结果。在做模拟测试的时候可以模拟路径，按照设计来规划，同时预期的结果可以通过数值分析看看是不是正确。

    分析一下control中的

    apollo_baidu-master/modules/control/testdata/lateral_controller_test/1_planning.pb.txt文件。

    这个文件是测试文件，记录了一段完整的规划路径。这个文件是txt文件格式，可以通过protobuf的API解析。【Apollo中的proto消息太多，又相互include。所以编译的时候发现proto转换后的.cc文件太多，编译太费事。其实可以学习百度使用Bazel的编译方式，每个最小化模块都编译为动态库。只要做增量编译就行，缩短了后续编译的时间。】

    首先解析的X,Y的笛卡尔坐标：

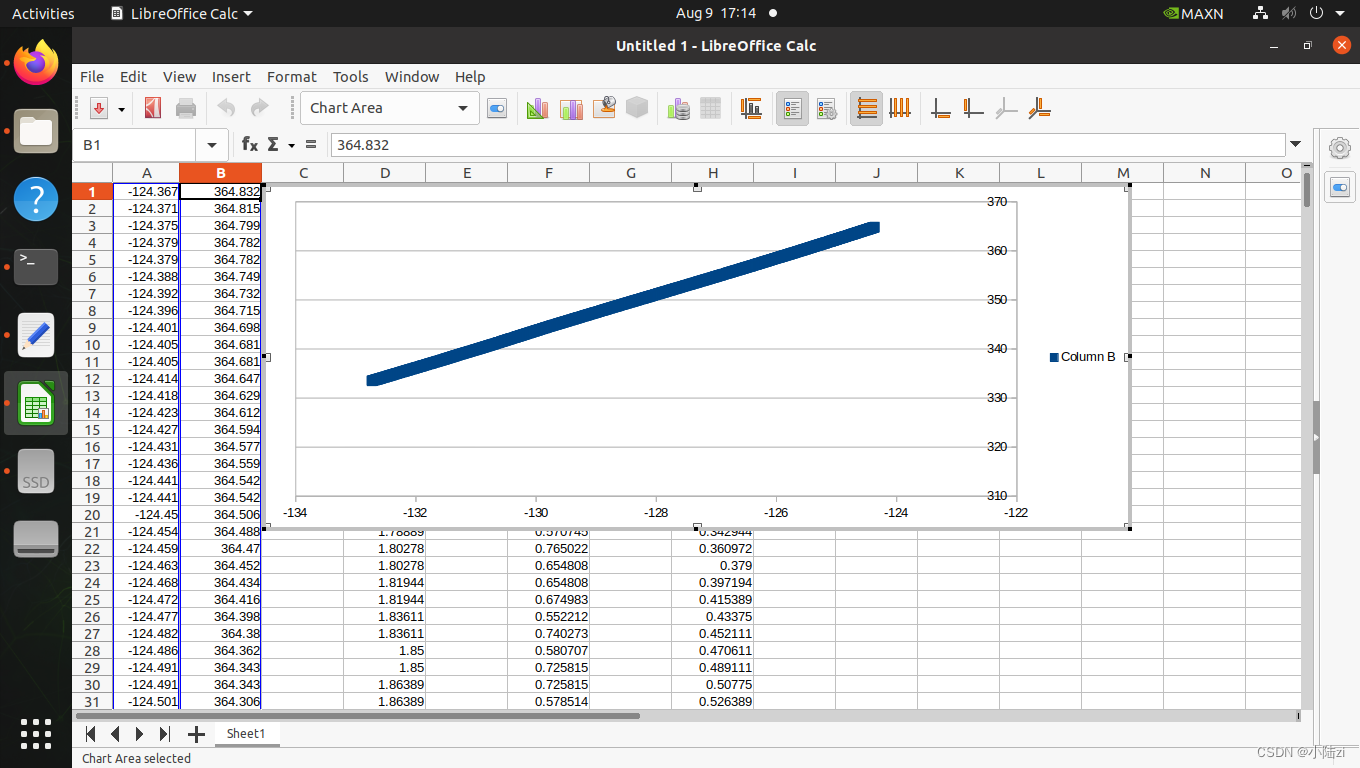
     发现是一条近似的直线，也验证了这条规划轨迹是做纵向控制的。这个图的坐标单位没有统一，所以无法从图片中获取斜率。斜率的计算比较粗略。应为认为是直线，在线上任取三个点，三个点分别和前一个点（path_point）做delt（x）和delt（y）,随后求出delt（y）/delt（x）。计算出斜率：3.681。

    其次看一下速度：

    速度从0时刻到424时刻也为线性增加，后面趋于平稳。可以后面的加速度做一下结合分析。

    加速度：

     V= a（t）的速度公式可以看出：随着时间的增加，只要a>0，么V是增加的。在0-104区间 加速度减小，128-250区间加速度增加。粗略看下速度的变化图：速度变化变得平缓。从区间 410开始到结束，加速度又波动，但是基本在没有加速的数值间震荡。通过速度图我们看到速度区域平缓，没有明显增加。

    这里有两个问题：

    （1）加速度抖动会不会影响直接的控车效果，车辆会不会出现抖动。

    （2）加速度数值和V的计算关系不能完全安V = a（t）来获取。可能要系数用来矫正，或者采样的精度不够。

    最后看下距离图：

    这应该就是S-T，距离的累加呈线性增加关系。表示车辆在坐标系的运动没有横向的的分量。做的直线运动。随着时间的增加，距离在增加。

     最后讲一下Frenet坐标系的理解。公式不推了网上很多。问题在为什么用这个笛卡尔和Frenet转换的公式，以及什么地方使用。

    SL坐标和frenet坐标系没有直接关系。frenet是自然坐标系的一种表示，就是把物体的运动做切向和法线方向的两个分解。在空间中还有第三个分量，垂直于平面的一个分量。和笛卡尔坐标系的关系如图：

    给定一个点，就可以判断这个点在参考线上的投影点之间的距离（法线方向），至于路程距离（S），其实没明白为什么可以通过参考线的frenet坐标推算出车辆行驶距离（S）。车辆完全可以不按照参考路径来行驶。

    XYZ就是笛卡尔坐标系，xyz就是运动轨迹上一点的切线和法线以及垂直这个平面的z向量。这个坐标系通过积分可以计算出曲线上两个点的距离。就是我们说的S。对于S求导可以得到速度，在对于S求二阶导可以得到加速度。

    我们经常看到SL坐标系，这个坐标系仅仅只是和frenet的计算结果有关系（距离）。这里推荐一篇“古月居”的博客，其中的效果图演示了SL的关系。

Frenet坐标系下的无人车轨迹规划详细讲解与ROS实现 - 古月居 (guyuehome.com)

   S代表了路程的的累加，如同前文分析的情况：当车辆直线匀速运动时，S会随时间的增加呈线性增加的关系。这里其实还有一点当车辆沿直线变加速度后，虽然法线方向没有分量，但是单位时间内行驶的距离一定会变化，因此S的斜率会改变。SL坐标中的S变换不能体现出车辆的实际运行情况。只能判断行驶距离。应为ST的横坐标是时间，而SL的横坐标是参考点法线方向的距离。

   L代表了法线方向的位移距离，当法线方向有加速度后。L就会有数值（横向距离）。 这里开始疑惑了：参考线SL的坐标形式是曲线还是直线？希望知道的老师可以回答一下，谢谢。任意一个参考线上的点L的位移是0。

   可以看下这个函数内部如何使用公式。目睹其实求出S L 以及SL各自的导数。

void TrajectoryAnalyzer::ToTrajectoryFrame(const double x, const double y,
													const double theta, const double v,
													const PathPoint &ref_point,
													double *ptr_s, double *ptr_s_dot,
													double *ptr_d,
													double *ptr_d_dot) const 

    文章很多知识点还没有彻底说明白，如果有误欢迎指正交流，谢谢。

    随后推荐一篇文章：

    Frenet坐标系及其与笛卡尔坐标转换(1)原理 - 知乎 (zhihu.com)