opencv基础51-图像轮廓04-轮廓多种图形拟合讲解及示例

news2024/12/28 3:54:44

轮廓拟合（Contour Fitting）是指在图像处理中，通过一些数学模型或曲线拟合方法来近似描述图像中的轮廓。图像中的轮廓是指物体的边界，轮廓拟合可以用于提取、描述和分析物体的形状。

常用的轮廓拟合方法包括多项式拟合、贝塞尔曲线拟合、B样条曲线拟合等。这些方法可以用来找到一个与实际轮廓相符合的数学模型，从而更好地描述物体的形状。拟合后的曲线可以用于进一步的分析、测量、识别等任务。

轮廓拟合在图像处理的许多应用中都有用武之地，例如：

  1. 形状分析：通过对轮廓进行拟合，可以提取物体的形状特征，如圆形、椭圆形等。

  2. 物体检测：通过拟合物体的轮廓，可以检测出物体的存在并确定其位置。

  3. 目标跟踪：将物体的轮廓拟合到连续的图像帧中，可以实现目标的跟踪。

  4. 工业检测：在制造业中，通过拟合产品的轮廓来检测产品的形状和尺寸。

  5. 医学图像分析：在医学领域，可以通过对轮廓的拟合来测量病变的大小和形状。

  6. 计算机辅助设计：在CAD等领域，可以使用轮廓拟合来生成复杂的曲线和形状。

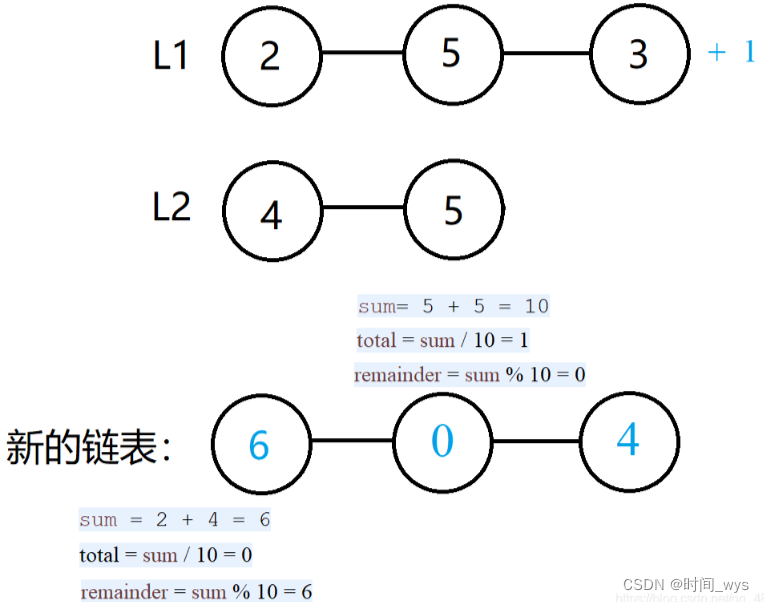
白话地说，轮廓拟合就是用数学上的曲线或者线条，来近似地描绘出一张图片里物体的边缘。就好像你在画画时，用一条线把物体的外形勾勒出来一样。通过这个近似的线条，我们可以更方便地分析物体的形状、大小，或者在图像中找到特定的物体。再看下面的示例图基本就明白什么是轮廓拟合了

在计算轮廓时，可能并不需要实际的轮廓，而仅需要一个接近于轮廓的近似多边形。
OpenCV 提供了多种计算轮廓近似多边形的方法。

矩形包围框

函数 cv2.boundingRect()能够绘制轮廓的矩形边界。该函数的语法格式为：

retval = cv2.boundingRect( array )

式中：

  • 返回值 retval 表示返回的矩形边界的左上角顶点的坐标值及矩形边界的宽度和高度。
  • 参数 array 是灰度图像或轮廓。

该函数还可以是具有 4 个返回值的形式：

x,y,w,h = cv2.boundingRect( array )

这里的 4 个返回值分别表示：

  • 矩形边界左上角顶点的 x 坐标。
  • 矩形边界左上角顶点的 y 坐标。
  • 矩形边界的 x 方向的长度。
  • 矩形边界的 y 方向的长度。

代码示例：显示函数 cv2.boundingRect()不同形式的返回值。

import cv2
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
#找到轮廓，返回的是轮廓的点集，以及它们的层次，contours是点集，hierarchy是层次，这里只有一个轮廓，所以只返回一个，用[0]取出来
contours, hierarchy = cv2.findContours(binary,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
#---------------返回顶点及边长------------------
x,y,w,h = cv2.boundingRect(contours[0])
print("顶点及长宽的点形式:")
print("x=",x)
print("y=",y)
print("w=",w)
print("h=",h)
#---------------仅有一个返回值的情况------------------
rect = cv2.boundingRect(contours[0])
print("\n 顶点及长宽的元组（tuple）形式：")
print("rect=",rect)

运行上述程序，显示如下结果：

顶点及长宽的点形式:
x= 202
y= 107
w= 157
h= 73
顶点及长宽的元组（tuple）形式：
rect= (202, 107, 157, 73)

示例2：使用函数 cv2.drawContours()绘制矩形包围框。

代码如下：

import cv2
import numpy as np
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)

#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
#---------------构造矩形边界------------------
x,y,w,h = cv2.boundingRect(contours[0])
brcnt = np.array([[[x, y]], [[x+w, y]], [[x+w, y+h]], [[x, y+h]]])
cv2.drawContours(o, [brcnt], -1, (255, 255,255), 1)
#---------------显示矩形边界------------------
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

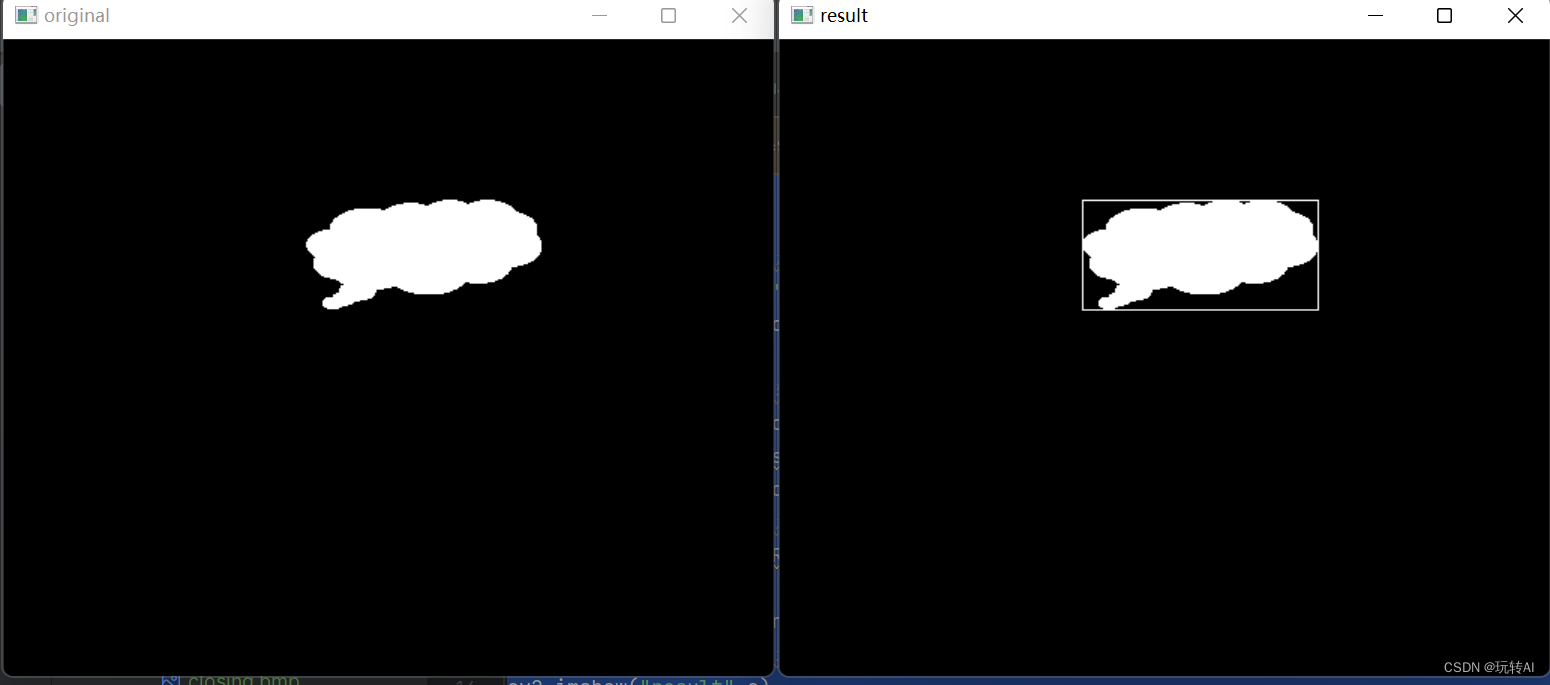
在这里插入图片描述
示例2另外一个函数的实现

示例3：使用函数 cv2.boundingRect()及 cv2.rectangle()绘制矩形包围框。

import cv2
#---------------读取并显示原始图像------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
#---------------提取图像轮廓------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
#---------------构造矩形边界------------------
x,y,w,h = cv2.boundingRect(contours[0])
cv2.rectangle(o,(x,y),(x+w,y+h),(255,255,255),2)

#---------------显示矩形边界------------------
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

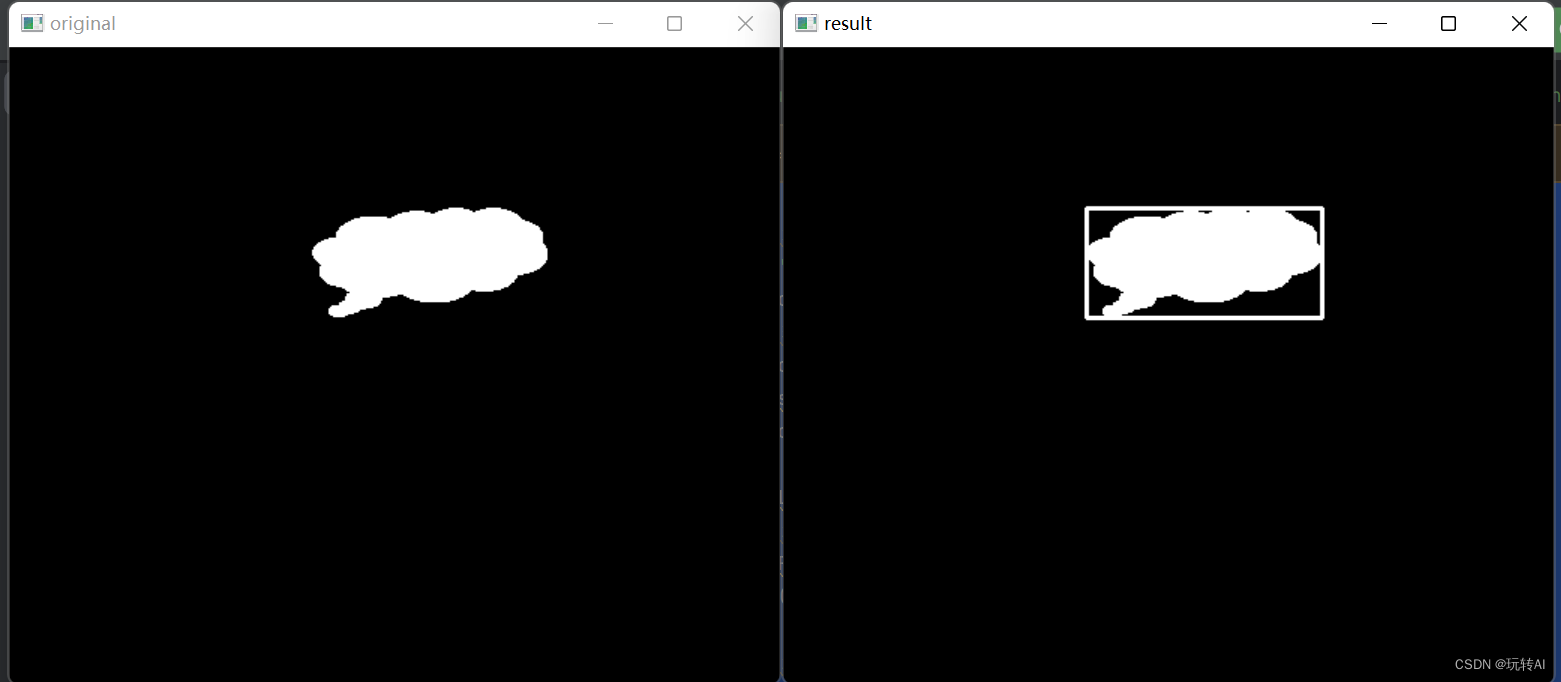
在这里插入图片描述

最小包围矩形框

函数 cv2.minAreaRect()能够绘制轮廓的最小包围矩形框，其语法格式为：

retval =cv2.minAreaRect( points )

式中：

  • 返回值 retval 表示返回的矩形特征信息。
    该值的结构是(最小外接矩形的中心(x,y),(宽度,高度),旋转角度)。
  • 参数 points 是轮廓。

需要注意，返回值 retval 的结构不符合函数 cv2.drawContours()的参数结构要求。因此，必须将其转换为符合要求的结构，才能使用。函数 cv2.boxPoints()能够将上述返回值 retval 转换为符合要求的结构。函数 cv2.boxPoints()的语法格式是：

points = cv2.boxPoints( box )

式中：

  • 返回值 points，是能够用于函数 cv2.drawContours()参数的轮廓点。
  • 参数 box 是函数 cv2.minAreaRect()返回值的类型的值。

示例：使用函数 cv2.minAreaRect()计算图像的最小包围矩形框。

import cv2
import numpy as np
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)

ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
rect = cv2.minAreaRect(contours[0])

print("返回值 rect:\n",rect)
points = cv2.boxPoints(rect)
print("\n 转换后的 points：\n",points)
points = np.int0(points) #取整
image=cv2.drawContours(o,[points],0,(255,255,255),1)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

返回值 rect:
 ((280.3700256347656, 138.58999633789062), (63.781028747558594, 154.99778747558594), 81.8698959350586)

 转换后的 points：
 [[199.14005 117.98   ]
 [352.58002  96.06   ]
 [361.6     159.19998]
 [208.16003 181.12   ]]

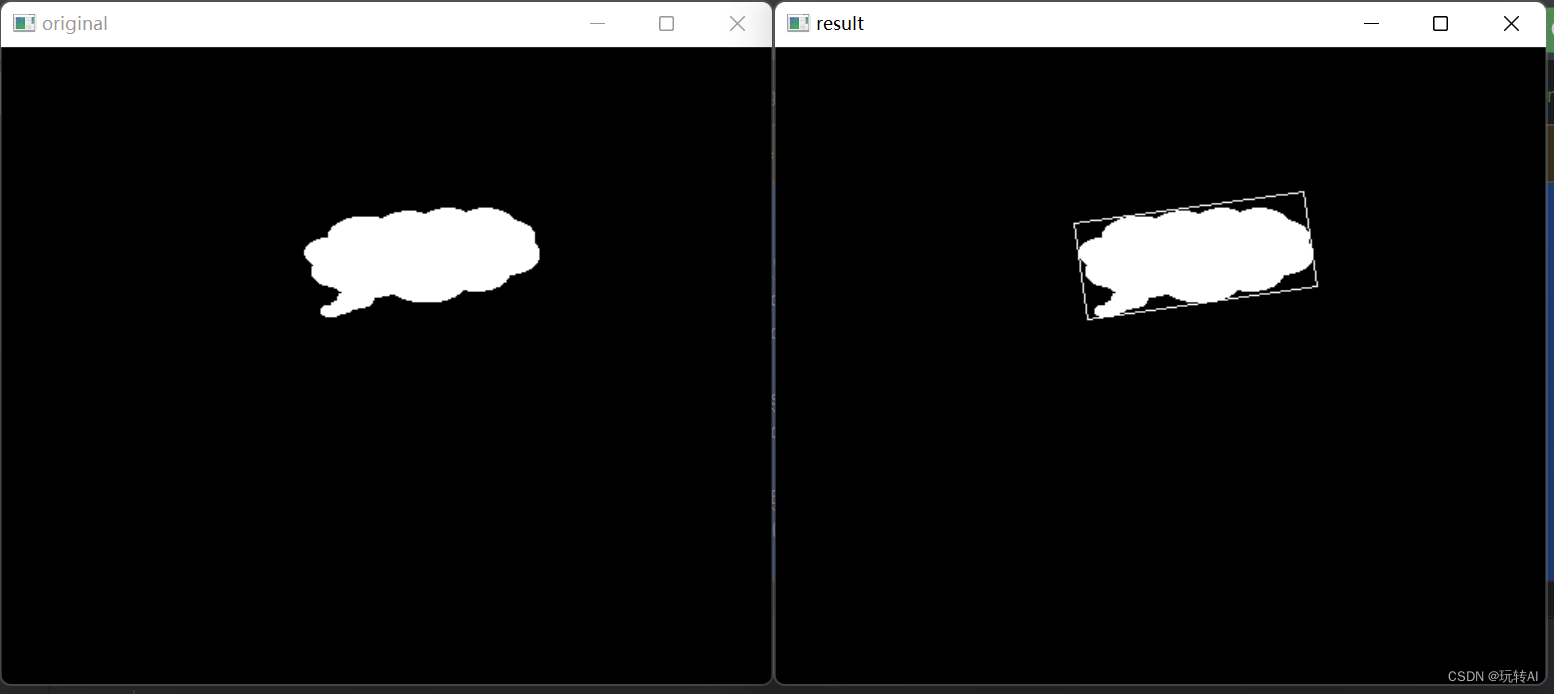
在这里插入图片描述
从输出结果可以看出：

  • 返回值 rect 表示返回的矩形特征信息。
    该值的结构是(最小外接矩形的中心(x,y),(宽度,高度),旋转角度)
  • 转换后的 points 是一些点，是能够用作函数 cv2.drawContours()参数的轮廓点。

最小包围圆形

函数 cv2.minEnclosingCircle()通过迭代算法构造一个对象的面积最小包围圆形。该函数的
语法格式为：

center, radius = cv2.minEnclosingCircle( points )

式中：

  • 返回值 center 是最小包围圆形的中心。
  • 返回值 radius 是最小包围圆形的半径。
  • 参数 points 是轮廓。

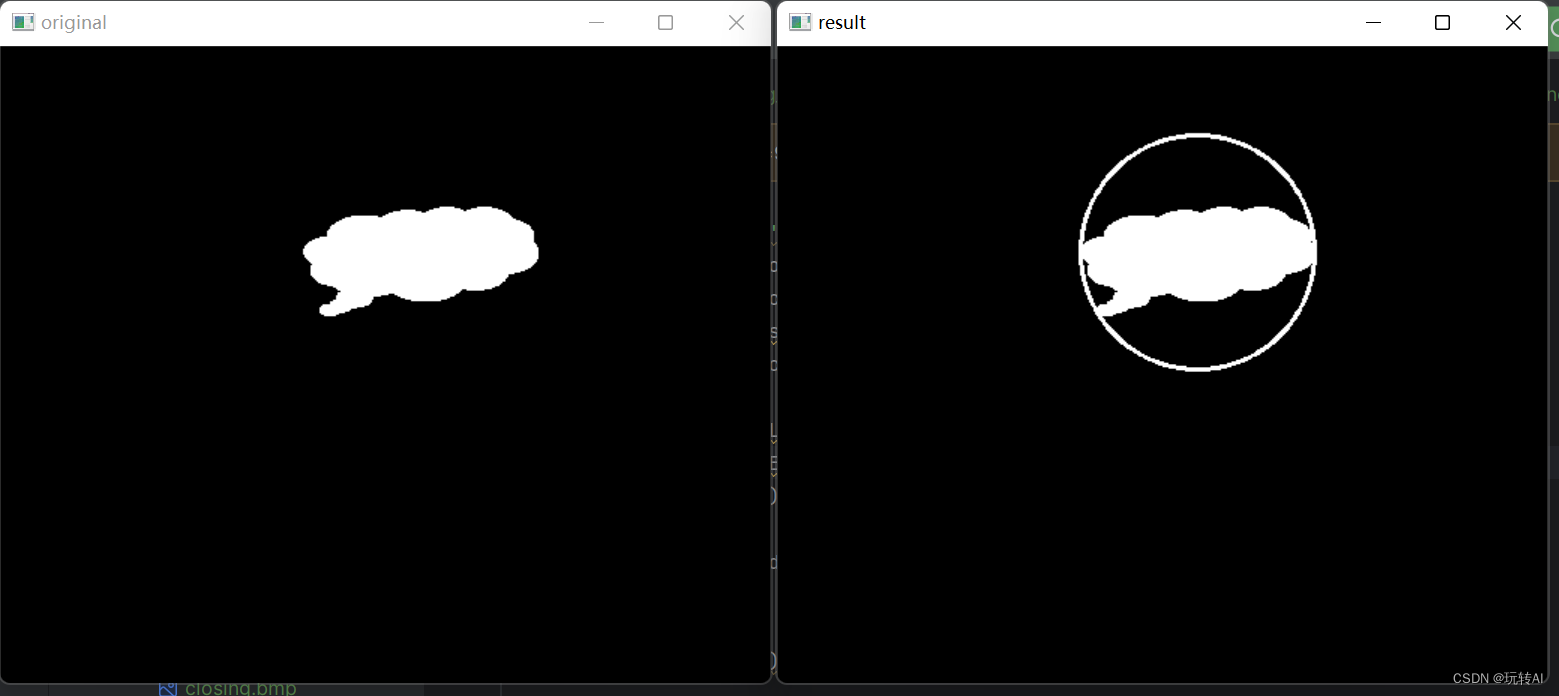
示例：使用函数 cv2.minEnclosingCircle()构造图像的最小包围圆形。

代码如下：

import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
(x,y),radius = cv2.minEnclosingCircle(contours[0])
center = (int(x),int(y))
radius = int(radius)
cv2.circle(o,center,radius,(255,255,255),2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行效果：
在这里插入图片描述

最优拟合椭圆

在 OpenCV 中，函数 cv2.fitEllipse()可以用来构造最优拟合椭圆。该函数的语法格式是：

retval = cv2.fitEllipse( points )

式中：

  • 返回值 retval 是 RotatedRect 类型的值。这是因为该函数返回的是拟合椭圆的外接矩形，retval 包含外接矩形的质心、宽、高、旋转角度等参数信息，这些信息正好与椭圆的中心点、轴长度、旋转角度等信息吻合。
  • 参数 points 是轮廓。

示例：使用函数 cv2.fitEllipse()构造最优拟合椭圆。

代码如下：

import cv2
o = cv2.imread('cc.bmp')
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
cv2.imshow("original",o)
ellipse = cv2.fitEllipse(contours[0])
print("ellipse=",ellipse)
cv2.ellipse(o,ellipse,(0,255,0),3)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

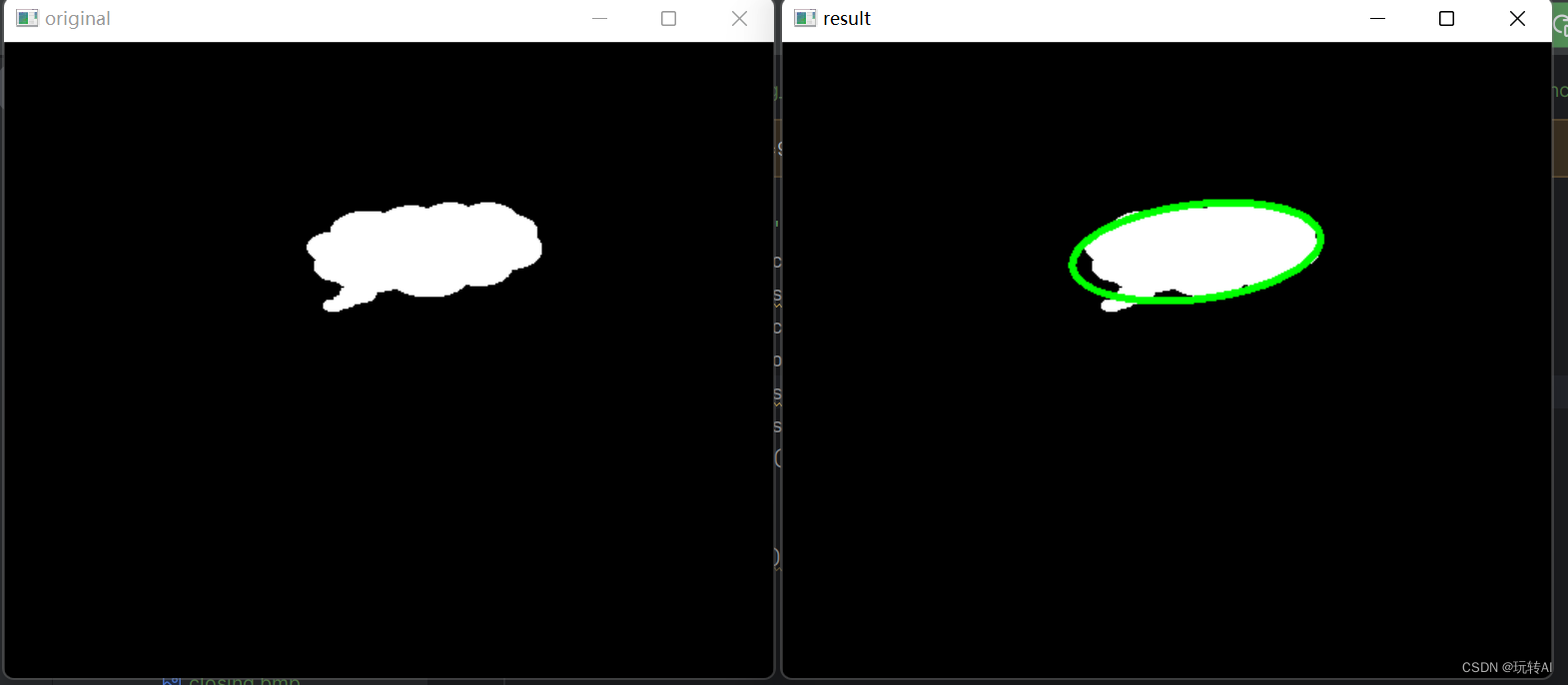
在这里插入图片描述
同时，程序还会显示如下的运行结果：

ellipse= ((276.2112731933594, 139.6067352294922), (63.01350021362305,
166.72308349609375), 82.60102844238281)

上述运行结果中：

  • (276.2112731933594, 139.6067352294922)是椭圆的中心点。
  • (63.01350021362305, 166.72308349609375)是椭圆的轴长度。
  • 82.60102844238281 是椭圆的旋转角度。

最优拟合直线

在OpenCV 中，函数 cv2.fitLine()用来构造最优拟合直线，该函数的语法格式为：

line = cv2.fitLine( points, distType, param, reps, aeps )

式中 line 为返回值，是返回的最优拟合直线参数。
式中的参数如下：

  • points：轮廓。
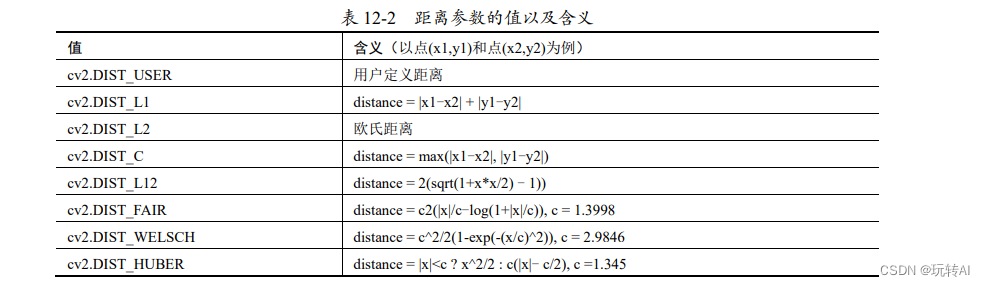
  • distType：距离类型。拟合直线时，要使输入点到拟合直线的距离之和最小，其类型如表 12- 2 所示。
  • param：距离参数，与所选的距离类型有关。当此参数被设置为 0 时，该函数会自动选择最优值。
  • reps：用于表示拟合直线所需要的径向精度，通常该值被设定为 0.01。
  • aeps：用于表示拟合直线所需要的角度精度，通常该值被设定为 0.01。

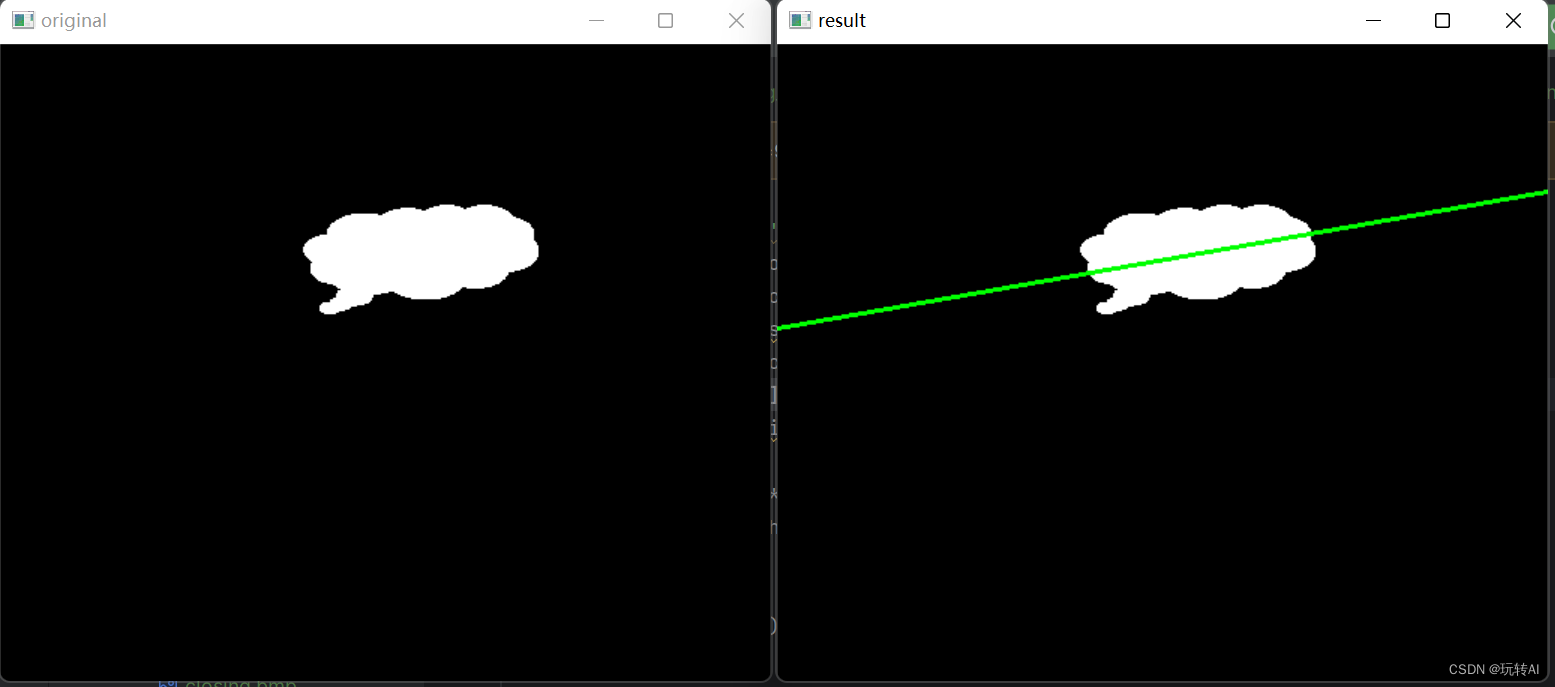
在这里插入图片描述

示例：使用函数 cv2.fitLine()构造最优拟合直线。

代码如下：

import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,cv2.RETR_LIST,cv2.CHAIN_APPROX_SIMPLE)
rows,cols = o.shape[:2]
[vx,vy,x,y] = cv2.fitLine(contours[0], cv2.DIST_L2,0,0.01,0.01)
lefty = int((-x*vy/vx) + y)
righty = int(((cols-x)*vy/vx)+y)
cv2.line(o,(cols-1,righty),(0,lefty),(0,255,0),2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：
在这里插入图片描述

最小外包三角形

在 OpenCV 中，函数 cv2.minEnclosingTriangle()用来构造最小外包三角形。该函数的语法格式为：

retval, triangle = cv2.minEnclosingTriangle( points )

式中有两个返回值：

  • retval：最小外包三角形的面积。
  • triangle：最小外包三角形的三个顶点集。
    式中的参数 points 是轮廓。

示例：使用函数 cv2.minEnclosingTriangle()构造最小外包三角形。

代码如下：

import cv2
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
cv2.CHAIN_APPROX_SIMPLE)
#
area,trgl = cv2.minEnclosingTriangle(contours[0])
print("area=",area)
print("trgl:",trgl)
for i in range(0, 3):
  cv2.line(o, tuple(trgl[i][0]),tuple(trgl[(i + 1) % 3][0]), (255,255,255), 2)
cv2.imshow("result",o)
cv2.waitKey()
cv2.destroyAllWindows()

运行报错：

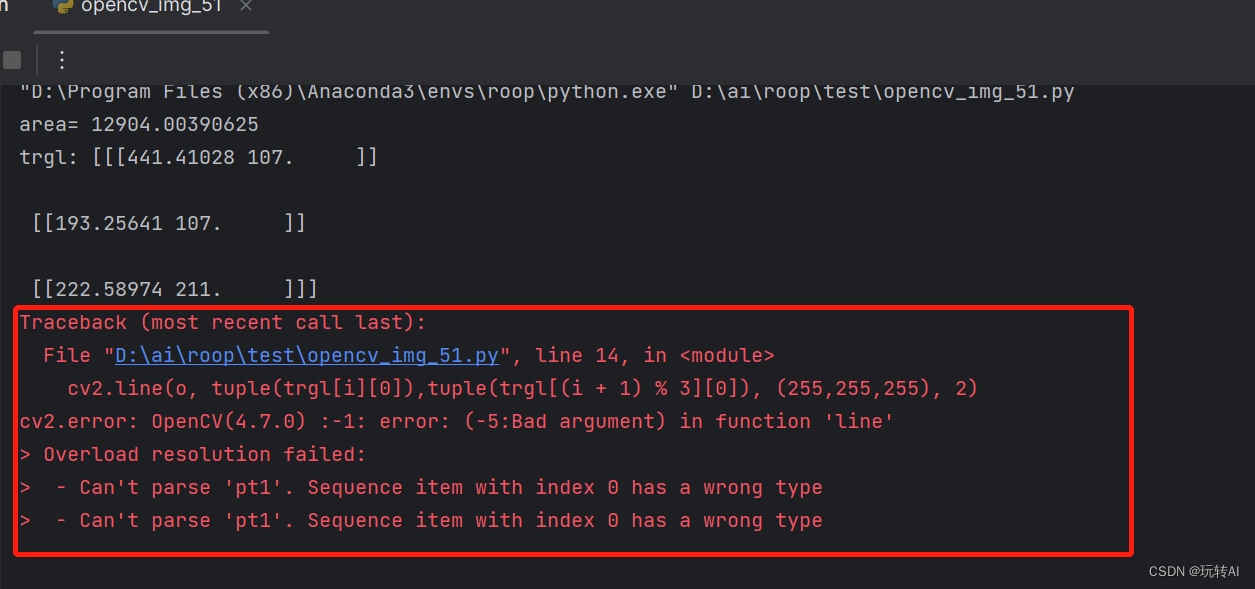
在这里插入图片描述
提示我们opecv4.7 这个版本里line 这个函数传入的参数值类型变了，现在的类型不支持。我们转换一下类型再试试

代码如下：

import cv2

o = cv2.imread('cc.bmp')
cv2.imshow("original", o)
gray = cv2.cvtColor(o, cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray, 127, 255, cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
                                       cv2.RETR_LIST,
                                       cv2.CHAIN_APPROX_SIMPLE)
#
area, trgl = cv2.minEnclosingTriangle(contours[0])
print("area=", area)
print("trgl:", trgl)
for i in range(0, 3):
    original_coordinate = tuple(trgl[i][0])
    original_coordinate2 = tuple(trgl[(i + 1) % 3][0])
    # 将坐标的每个分量分别转换为整数
    x_int = int(original_coordinate[0])
    y_int = int(original_coordinate[1])
    x_int2 = int(original_coordinate2[0])
    y_int2 = int(original_coordinate2[1])
    # 将坐标转换为整数,
    coordinate_as_int = (x_int, y_int)
    coordinate_as_int2 = (x_int2, y_int2)

    cv2.line(o, coordinate_as_int, coordinate_as_int2, (255, 255, 255), 2)
cv2.imshow("result", o)
cv2.waitKey()
cv2.destroyAllWindows()

运行结果如下：

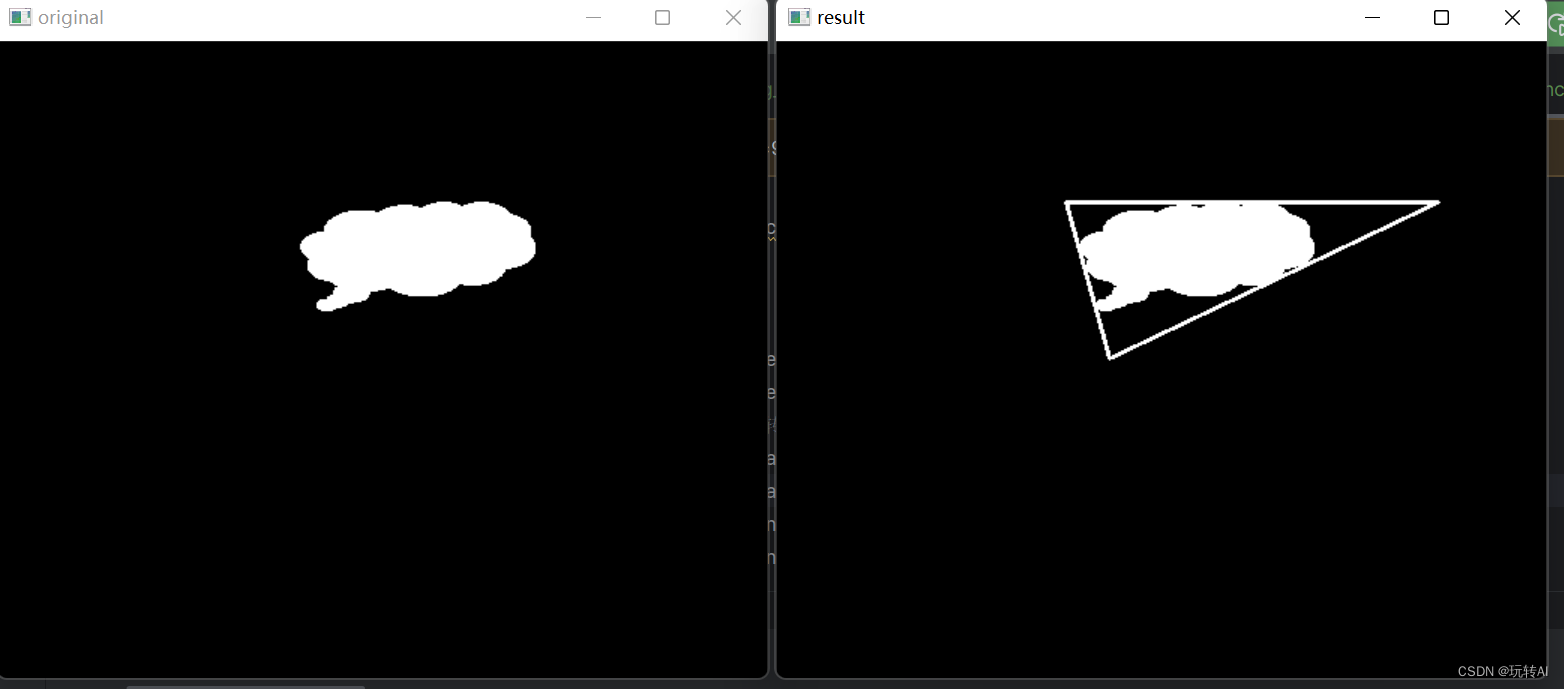
在这里插入图片描述
从上述结果可以看出：

  • 返回值 area 是最小外包三角形的面积。
  • 返回值 trgl 是最小外包三角形的三个顶点。

逼近多边形

函数 cv2.approxPolyDP()用来构造指定精度的逼近多边形曲线。该函数的语法格式为：

approxCurve = cv2.approxPolyDP( curve, epsilon, closed )

式中，返回值 approxCurve 为逼近多边形的点集。

式中的参数如下：

  • curve 是轮廓。
  • epsilon 为精度，原始轮廓的边界点与逼近多边形边界之间的最大距离。
  • closed 是布尔型值。该值为 True 时，逼近多边形是封闭的；否则，逼近多边形是不封闭的。
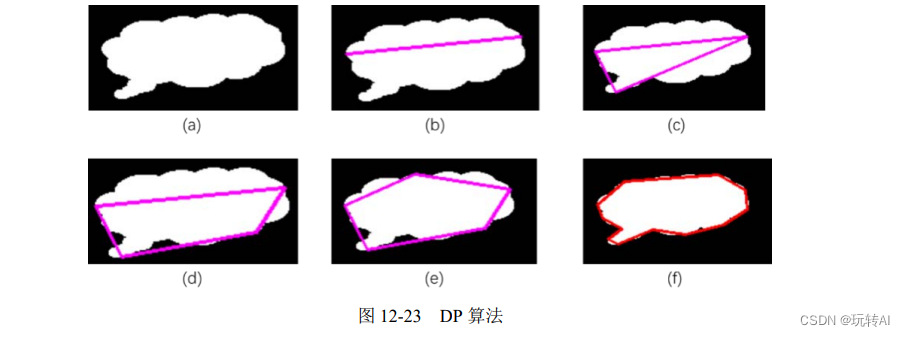
    函数 cv2.approxPolyDP()采用的是 Douglas-Peucker 算法（DP 算法）。

以图 12-23 为例，该算法首先从轮廓中找到距离最远的两个点，并将两点相连（见图 12-23 的(b)图）。

接下来，在轮廓上找到一个离当前直线最远的点，并将该点与原有直线连成一个封闭的多边形，此时得到一个三角形，如图 12-23 中的©图所示。

将上述过程不断地迭代，将新找到的距离当前多边形最远的点加入到结果中。当轮廓上所有的点到当前多边形的距离都小于函数 cv2.approxPolyDP()的参数 epsilon 的值时，就停止迭代。最终可以得到如图 12-23 的(f)图所示的处理结果。

通过上述过程可知，epsilon 是逼近多边形的精度信息。通常情况下，将该精度设置为多边形总长度的百分比形式。

在这里插入图片描述

示例：使用函数 cv2.approxPolyDP()构造不同精度的逼近多边形。

代码如下：

import cv2
#----------------读取并显示原始图像-------------------------------
o = cv2.imread('cc.bmp')
cv2.imshow("original",o)
#----------------获取轮廓-------------------------------
gray = cv2.cvtColor(o,cv2.COLOR_BGR2GRAY)
ret, binary = cv2.threshold(gray,127,255,cv2.THRESH_BINARY)
contours, hierarchy = cv2.findContours(binary,
 cv2.RETR_LIST,
 cv2.CHAIN_APPROX_SIMPLE)
#----------------epsilon=0.1*周长-------------------------------
adp = o.copy()
epsilon = 0.1*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.1",adp)
#----------------epsilon=0.09*周长-------------------------------
adp = o.copy()
epsilon = 0.09*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.09",adp)
#----------------epsilon=0.055*周长-------------------------------
adp = o.copy()
epsilon = 0.055*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.055",adp)
#----------------epsilon=0.05*周长-------------------------------
adp = o.copy()
epsilon = 0.05*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.05",adp)
#----------------epsilon=0.02*周长-------------------------------
adp = o.copy()
epsilon = 0.02*cv2.arcLength(contours[0],True)
approx = cv2.approxPolyDP(contours[0],epsilon,True)
adp=cv2.drawContours(adp,[approx],0,(0,0,255),2)
cv2.imshow("result0.02",adp)
#----------------等待释放窗口-------------------------------
cv2.waitKey()
cv2.destroyAllWindows()

运行结果：

在这里插入图片描述
从程序运行结果可以看出，在函数 cv2.approxPolyDP()中通过参数 epsilon 可以控制逼近多边形的精度。
需要注意：本节中使用的图像都是仅有一个轮廓的图像，处理的轮廓都是 contours[0]。如果处理的原图像中有多个轮廓，则需要注意控制轮廓的索引，即 contours[i]中的 i 值，使其指向特定的轮廓。

实验原图

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/856193.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【刷题笔记8.9】LeetCode题目：两数相加

【刷题笔记8.9】LeetCode题目：两数相加

LeetCode题目2：两数相加 题目及描述 给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。 请你将两个数相加，并以相同形式返回一个表示和的链表。 你可以假设…
阅读更多...
后端开发10.规格模块

后端开发10.规格模块

概述 简介 效果图 <
阅读更多...
【uniapp】封装一个全局自定义的模态框

【uniapp】封装一个全局自定义的模态框

【需求描述】 在接口401处&#xff0c;需要实现全局提示并弹出自定义模态框的功能。考虑到uni-app内置的模态框和app原生提示框的自定义能力有限&#xff0c;我决定自行封装全局自定义的模态框&#xff0c;以此为应用程序提供更加统一且个性化的界面。 【效果图】 【封装】 主…
阅读更多...
Ansible Playbook快速部署一主多从MySQL集群

Ansible Playbook快速部署一主多从MySQL集群

部署目标&#xff1a; 1、快速部署一套一主两从的mysql集群 2、部署过程中支持交互式定义安装目录及监听端口号 部署清单目录结构&#xff1a; rootmaster:/opt/mysql# tree . . ├── group_vars │ └── all.yml ├── hosts ├── mysql.yml └── roles└── mys…
阅读更多...
两个状态的马尔可夫链

两个状态的马尔可夫链

手动推导如下公式。 证明&#xff1a; 首先将如下矩阵对角化&#xff1a; { 1 − a a b 1 − b } \begin {Bmatrix} 1-a & a \\ b & 1-b \end {Bmatrix} {1−ab​a1−b​} (1)求如下矩阵的特征值&#xff1a; { 1 − a a b 1 − b } { x 1 x 2 } λ { x 1 x 2 }…
阅读更多...
Android Https

Android Https

本质&#xff1a;在客户端和服务端使用非对称加密协商出一套对称密钥&#xff0c;每次发送数据前加密&#xff0c;收到后解密&#xff0c;达到加密传输 http ssl 在http之下增加了安全层&#xff0c;用于保障http的加密传输 HTTPS连接 TLS连接步骤 1.客户端发送 client h…
阅读更多...
Apache Doris 入门教程25：通过开启 Debug 日志进行性能分析

Apache Doris 入门教程25：通过开启 Debug 日志进行性能分析

Doris 的 FE 和 BE 节点的系统运行日志默认为 INFO 级别。通常可以满足对系统行为的分析和基本问题的定位。但是某些情况下&#xff0c;可能需要开启 DEBUG 级别的日志来进一步排查问题。本文档主要介绍如何开启 FE、BE节点的 DEBUG 日志级别。 不建议将日志级别调整为 WARN 或…
阅读更多...
一维二维数组的指针于sizeof和strlen

一维二维数组的指针于sizeof和strlen

目录 一维数组于指针的一些题二维数组于指针的一些题 一维数组于指针的一些题 对数组名的理解 数组名表示首元素地址 //两个例外&#xff1a; //sizeof&#xff08;数组名&#xff09;:表示计算整个数组的大小 //&数组名&#xff1a;这里取的也是整个数组的大小,除了他两以…
阅读更多...
ArcGIS、ENVI、InVEST、FRAGSTATS技术教程

ArcGIS、ENVI、InVEST、FRAGSTATS技术教程

专题一 空间数据获取与制图 1.1 软件安装与应用讲解 1.2 空间数据介绍 1.3海量空间数据下载 1.4 ArcGIS软件快速入门 1.5 Geodatabase地理数据库 专题二 ArcGIS专题地图制作 2.1专题地图制作规范 2.2 空间数据的准备与处理 2.3 空间数据可视化&#xff1a;地图符号与注…
阅读更多...
23.8.9总结

23.8.9总结

接下来是答辩后的完善&#xff1a; 轮播图在管理员处可以进行修改&#xff0c; 消息处用websocket实现实时更新&#xff0c; 管理员审核界面&#xff0c;未审核的文章不能点赞&#xff0c;评论&#xff0c;收藏&#xff0c;不能用前端页面&#xff0c; 评论用二级评论&…
阅读更多...
(el-Table)操作：Element-plus 中Table 表格组件：多选修改成支持单选及表格相关样式的调整

(el-Table)操作：Element-plus 中Table 表格组件：多选修改成支持单选及表格相关样式的调整

Ⅰ、Element-plus 提供的 Table 表格组件与想要目标情况的对比&#xff1a; 1、Element-plus 提供 Table 组件情况&#xff1a; 其一、Element-ui 自提供的 Table 代码情况为(示例的代码)&#xff1a; // Element-plus 自提供的代码&#xff1a; // 此时是使用了 ts 语言环境…
阅读更多...
.NET根据类的值进行序列化反序列化操作

.NET根据类的值进行序列化反序列化操作

前言&#xff1a; 在.NET种&#xff0c;序列化一般常用的方式是使用Newtonsoft.Json进行序列化和反序列化操作&#xff0c;比如创建一个Person类 public class Person {public string Name { get; set; }public int Age { get; set; } }序列化为json // 对象序列化为 JSONPe…
阅读更多...
vuejs 设计与实现 - 快速diff算法

vuejs 设计与实现 - 快速diff算法

Vue.js 2 所采用的双端 Diff 算法。既然快速 Diff 算法如此高效&#xff0c;我们有必要了解它的思路。接下来&#xff0c;我们就着重讨论快速 Diff 算法的实现原理。 相同的前置元素和后置元素 快速 Diff 算法借鉴了纯文本 Diff 算法中预处理的步骤。 案例&#xff1a; 旧的…
阅读更多...
数据结构-队列（C语言的简单实现）

数据结构-队列（C语言的简单实现）

简介 队列也是一种数据结构&#xff0c;队列也可以用来存放数字每次只能向队列里将入一个数字&#xff0c;每次只能从队列里获得一个数字在队列中&#xff0c;允许插入的一段称为入队口&#xff0c;允许删除的一段称为出队口它的原则是先进先出(FIFO: first in first out)&…
阅读更多...
Java8实战-总结15

Java8实战-总结15

Java8实战-总结15 引入流流简介流与集合 引入流 流简介 要讨论流&#xff0c;先来谈谈集合&#xff0c;这是最容易上手的方式。Java 8中的集合支持一个新的stream方法&#xff0c;它会返回一个流(接口定义在java.util.stream.Stream里)。在后面会看到&#xff0c;还有很多其他…
阅读更多...
自从学了C++之后，小雅兰就有对象了！！！（类与对象）（中）——“C++”

自从学了C++之后，小雅兰就有对象了！！！（类与对象）（中）——“C++”

各位CSDN的uu们好呀&#xff0c;好久没有更新小雅兰的C专栏啦&#xff0c;话不多说&#xff0c;让我们进入类和对象的世界吧&#xff01;&#xff01;&#xff01; 类的6个默认成员函数 构造函数 析构函数 拷贝构造函数 类的6个默认成员函数 如果一个类中什么成员都没有&am…
阅读更多...
C 语言中，「.」与「-＞」有什么区别？

C 语言中，「.」与「-＞」有什么区别？

使用“.”的话&#xff0c;只需要声明一个结构体。格式是结构体类型名结构体名。然后通过结构体名加上“.”再加上域名&#xff0c;就可以引用结构体的域了。因为结构体的内存是自动分配的&#xff0c;就像使用int a;一样。而使用“->”的话&#xff0c;需要声明一个结构体的…
阅读更多...
【三维编辑】Seal-3D：基于NeRF的交互式像素级编辑

【三维编辑】Seal-3D：基于NeRF的交互式像素级编辑

文章目录 摘要一、引言二、方法2.1.基于nerf的编辑问题概述2.2.编辑指导生成2.3.即时预览的两阶段学生训练 三、实验总结 项目主页: https://windingwind.github.io/seal-3d/ 代码&#xff1a;https://github.com/windingwind/seal-3d/ 论文: https://arxiv.org/pdf/2307.15131…
阅读更多...
vue3 动态导入src/page目录下的所有子文件，并自动注册所有页面组件

vue3 动态导入src/page目录下的所有子文件，并自动注册所有页面组件

main.js添加一下代码&#xff1a; const importAll (modules) > {Object.keys(modules).forEach((key) > {const component key.replace(/src/, /).replace(.vue, );const componentName key.split(/).slice(-2, -1)[0] -page;app.component(componentName, modules…
阅读更多...
Vue2-简介、模板语法、数据绑定、MVVM、数据代理、事件处理

Vue2-简介、模板语法、数据绑定、MVVM、数据代理、事件处理

&#x1f954;&#xff1a;成功之后就能光明正大地回望所有苦难 VUE-Day1 Vue简介1、Vue是什么&#xff1f;2、谁开发的&#xff1f; 发展历程&#xff1f;3、Vue的特点4、容器和实例、实例中的el和data总结 Vue模板语法插值语法指令语法 数据绑定1.单向数据绑定&#xff08;v-…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023