4 代码实现二叉树的非递归遍历

在“2 二叉树的遍历方法”中提到，二叉树的遍历方法有前序遍历、中序遍历、后序遍历属于深度优先遍历。接下来以前序遍历为例，通过代码实现该方法的二叉树非递归遍历。

4.1 前序遍历

4.1.1 前序遍历的非递归步骤

因为前序遍历的输出顺序是根节点、左子树、右子树，所以以前序的方式遍历图1所示的二叉树，则输出的顺序应为“1->2->4->5->3->6”。

前序遍历的非递归的流程图如图2所示。

图2 前序遍历的非递归流程图

从图1的根节点（值为1的节点）开始，根据图2的流程图，可以得到如图3所示的步骤。

图3 前序遍历的非递归步骤图

从图3的步骤图中可知，输出的数据是“1 2 3 5 3 6”，即前序遍历。

4.1.2 前序遍历的非递归的实现

前序遍历的非递归代码如下所示。

void preOrderTraveralWithStack(TreeNode* root)

{

    stack<TreeNode*> stk;

    TreeNode* treeNode = root;

    while (treeNode != NULL || !stk.empty())

    {

        while (treeNode != NULL)

        {

            cout << treeNode->data<<endl;

            stk.push(treeNode);

            treeNode = treeNode->leftChild;

        }

        if (!stk.empty())

        {

            treeNode = (TreeNode*)stk.top();

            treeNode = treeNode->rightChild;

            stk.pop();

        }

    }

}

其中，preOrderTraveralWithStackstk()函数的参数root是起始节点，即根节点。在该函数中，stk是自定义结构TreeNode的栈，可结合图1、图2和图3理解以上代码。

在主函数中，使用“3.3 关联节点”中提到的代码创建节点和关联节点之后，调用preOrderTraveralWithStackstk()函数即可实现前序遍历。

preOrderTraveralWithStack(treenode1);

其中，treenode1是图1中的根节点。代码输出的结果如图4所示。

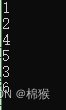
图4 前序遍历代码输出

4.2 中序遍历

中序遍历的输出顺序是左子树、根节点、右子树。因此，对于图1所示的节点图，采用中序遍历的输出结果是“4->2->5->1->3->6”。前序遍历的非递归的流程图如图5所示。

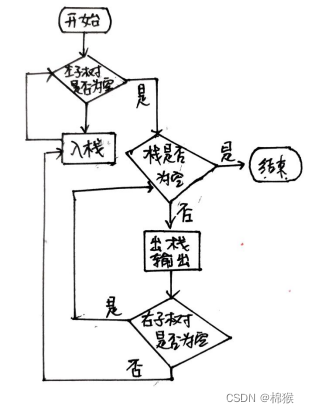
图5 中序遍历的非递归流程图

中序遍历实现的代码如下所示。

void inOrderTraveralWithStack(TreeNode* root)

{

    stack<TreeNode*> stk;

    TreeNode* treeNode = root;

    while (treeNode != NULL || !stk.empty())

    {

        while (treeNode != NULL)

        {

            stk.push(treeNode);

            treeNode = treeNode->leftChild;

        }

        if (!stk.empty())

        {

            treeNode = (TreeNode*)stk.top();

            cout << treeNode->data << endl;

            treeNode = treeNode->rightChild;

            stk.pop();

        }

    }

}

中序遍历的代码输出如图6所示。

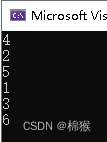
图6 中序遍历代码输出

4.3 后序遍历

中序遍历的输出顺序是左子树、右子树、根节点。因此，对于图1所示的节点图，采用中序遍历的输出结果是“4->5->2->6->3->1”。前序遍历的非递归的流程图如图7所示。

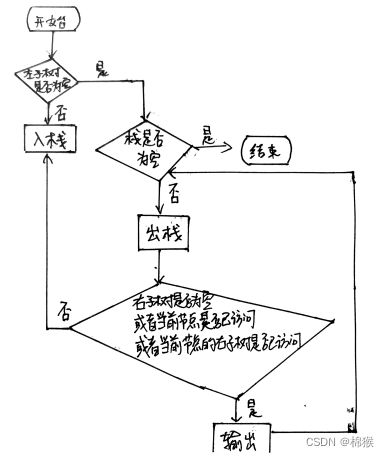
图7 后序遍历的非递归流程图

后序遍历实现的代码如下所示。

void postOrderTraveralWithStack(TreeNode* root)

{

    stack<TreeNode*> stk;

    TreeNode* treeNode = root;

    TreeNode* lastVisit = nullptr;

    while (treeNode != nullptr || !stk.empty())

    {

        while (treeNode != nullptr)

        {

            stk.push(treeNode);

            treeNode = treeNode->leftChild;

        }

        if (!stk.empty())

        {

            treeNode = (TreeNode*)stk.top();

            stk.pop();

            if (treeNode->rightChild == nullptr || treeNode == lastVisit || treeNode->rightChild == lastVisit)

            {

                cout << treeNode->data << endl;

                lastVisit = treeNode;

                treeNode = nullptr;

            }

            else

            {

                stk.push(treeNode);

                treeNode = treeNode->rightChild;

            }           

        }

    }

}

后序遍历的代码输出如图8所示。