Python-OpenCV中的图像处理-图像金字塔
- 图像金字塔
- 高斯金字塔
- 拉普拉斯金字塔
- 金字塔图像融合
图像金字塔
- 同一图像的不同分辨率的子图集合,如果把最大的图像放在底部,最小的放在顶部,看起来像一座金字塔,故而得名图像金字塔。
- cv2.pyrUp():上采样
- cv2.pyrDown():下采样
高斯金字塔
高斯金字塔的顶部是通过将底部图像中的连续的行和列去除得到的。顶部图像中的每个像素值等于下一层图像中 5 个像素的高斯加权平均值。这样操作一次一个 MxN 的图像就变成了一个 M/2xN/2 的图像。所以这幅图像的面积就变为原来图像面积的四分之一。这被称为 Octave。连续进行这样的操作我们就会得到一个分辨率不断下降的图像金字塔。我们可以使用函数cv2.pyrDown() 和 cv2.pyrUp() 构建图像金字塔。
import numpy as np
import cv2
from matplotlib import pyplot as plt
# 图像金字塔 :同一图像的不同分辨率的子图集合
# 有两种:高斯金字塔(Gaussian Pyramid) 和 拉普拉斯金字塔(Pyramid)
# 高斯金字塔 每次处理后图像的面积变为原来的四分之一,也被称为Octave
# cv2.pyrDown() #分辨率降低
# cv2.pyrUp() #分辨率增高
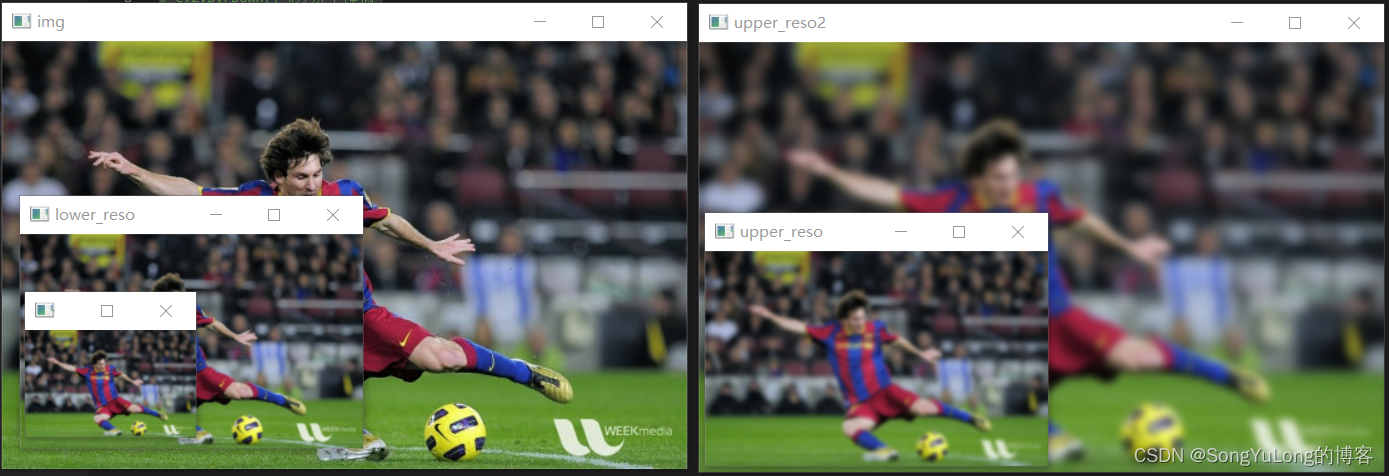
img = cv2.imread('./resource/opencv/image/messi5.jpg')
lower_reso = cv2.pyrDown(img)
lower_reso2 = cv2.pyrDown(lower_reso)
upper_reso = cv2.pyrUp(lower_reso2)
upper_reso2 = cv2.pyrUp(upper_reso)
cv2.imshow('img', img)
cv2.imshow('lower_reso', lower_reso)
cv2.imshow('lower_reso2', lower_reso2)
cv2.imshow('upper_reso', upper_reso)
cv2.imshow('upper_reso2', upper_reso2)
cv2.waitKey(0)
cv2.destroyAllWindows()
拉普拉斯金字塔
拉普拉斯金字塔可以有高斯金字塔计算得来,公式如下:
Li = Gi - pyrUp( Gi + 1 )
式中:
- Li:表示拉普拉斯金字塔中的第i层
- Gi:表示高斯金字塔中的第i层
拉普拉金字塔的图像看起来就像边界图,其中很多像素都是 0。他们经常
被用在图像压缩中。
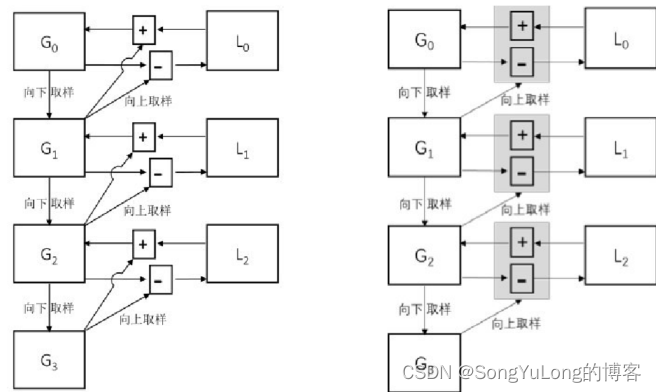
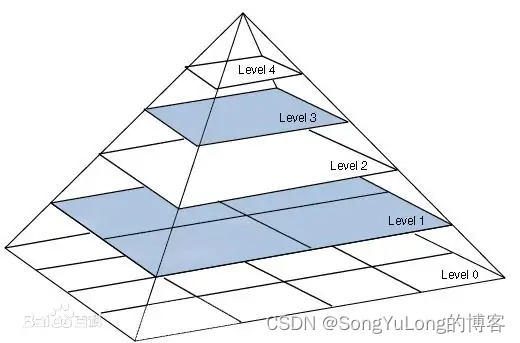
图中各标记含义如下:
- G0、G1、G2、G3分别是高斯金字塔的第0层、第1层、第2层、第3层。
- L0、L1、L2、分别是拉普拉斯金字塔的第0层、第1层、第2层。
- 向下的箭头表示向下采样操作(对应cv2.pyrDown()函数)
- 向右的箭头表示向上采样操作(对应cv2.pyrUp() 函数)
- "+"表示加法操作
- "-"表示减法操作
上图中的操作关系有:
向下采样:
- G1 = cv2.pyrDown(G0)
- G2 = cv2.pyrDown(G1)
- G3 = cv2.pyrDown(G2)
拉普拉斯金字塔:
- L0 = G0 - cv2.pyrUp(G1)
- L1 = G1 - cv2.pyrUp(G2)
- L2 = G2 - cv2.pyrUp(G3)
向上采样恢复高分辨率图像:
- G0 = L0 + cv2.pyrUp(G1)
- G1 = L1 + cv2.pyrUp(G2)
- G2 = L2 + cv2.pyrUp(G3)
上述关系是通过数学运算推导得到的。例如,已知L0=G0-cv2.pyrUp(G1),将表达式右侧的cv2.pyrUp(G1)移到左侧,就得到了表达式G0 = L0 + cv2.pyrUp(G1)。除此之外,G1和G2都可以通过拉普拉斯金字塔的构造表达式得到。如之前介绍的,拉普拉斯金字塔的目的就是为了恢复高分辨率的图像。
# 拉普拉斯金字塔构建
G0 = cv2.imread("./resource/opencv/image/lena.jpg")
cv2.imshow("input image",G0)
G1=cv2.pyrDown(G0)
G2=cv2.pyrDown(G1)
G3=cv2.pyrDown(G2)
G4=cv2.pyrDown(G3)
L0 = cv2.subtract(G0,cv2.pyrUp(G1))
L1 = cv2.subtract(G1,cv2.pyrUp(G2))
L2 = cv2.subtract(G2,cv2.pyrUp(G3))
L3 = cv2.subtract(G3,cv2.pyrUp(G4))
cv2.imshow("G1",G1)
cv2.imshow("G2",G2)
cv2.imshow("G3",G3)
cv2.imshow("G4",G4)
cv2.waitKey(0)
cv2.destroyAllWindows()
import numpy as np
import cv2
# 拉普拉斯金字塔是由高斯金字塔计数得到,公式如下
# Li = Gi - PyrUP(PyrDown(Gi))
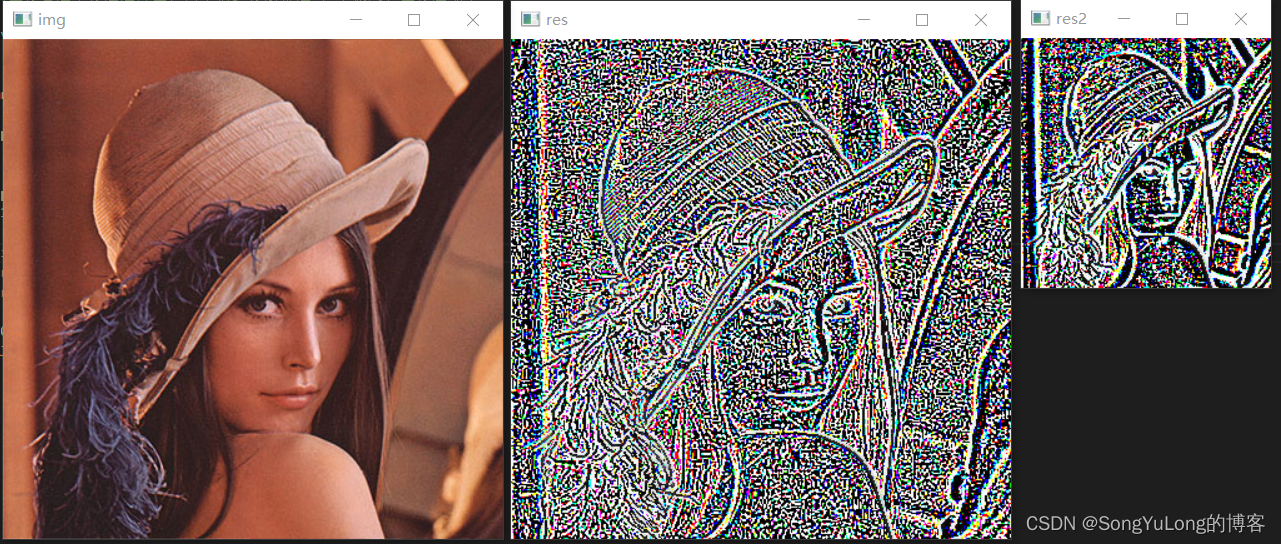
# 拉普拉斯金字塔图像看起来像是边界图,其中很多像素都是0,常被用在图像压缩中。
import cv2 as cv
if __name__ == '__main__':
img = cv.imread("./resource/opencv/image/lena.jpg")
down1 = cv.pyrDown(img)
res = img - cv.pyrUp(down1)
down2 = cv.pyrDown(down1)
res2 = down1 - cv.pyrUp(down2)
cv.imshow("img", img)
cv.imshow("res", res)
cv.imshow("res2", res2)
cv.waitKey(0)
cv.destroyAllWindows()
金字塔图像融合
import numpy as np
import cv2
import sys
# 实现上述效果的步骤如下:
# 1. 读入两幅图像,苹果和橘子
# 2. 构建苹果和橘子的高斯金字塔( 6 层)
# 3. 根据高斯金字塔计算拉普拉斯金字塔
# 4. 在拉普拉斯的每一层进行图像融合(苹果的左边与橘子的右边融合)
# 5. 根据融合后的图像金字塔重建原始图像。
A = cv2.imread('./resource/opencv/image/apple.jpg')
B = cv2.imread('./resource/opencv/image/orange.jpg')
print(A.shape)
print(B.shape)
# 生成高斯金字塔
G = A.copy()
gpA = [G]
for i in range(5):
G = cv2.pyrDown(G)
gpA.append(G)
G = B.copy()
gpB = [G]
for i in range(5):
G = cv2.pyrDown(G)
gpB.append(G)
# 产生Laplacian金字塔
lpA = [gpA[5]]
for i in range(5,0,-1):
GE = cv2.pyrUp(gpA[i])
L = cv2.subtract(gpA[i-1],GE)
lpA.append(L)
lpB = [gpB[5]]
for i in range(5,0,-1):
GE = cv2.pyrUp(gpB[i])
L = cv2.subtract(gpB[i-1],GE)
lpB.append(L)
# 合并
LS = []
for la,lb in zip(lpA,lpB):
rows,cols,dpt = la.shape
ls = np.hstack((la[:,0:cols//2], lb[:,cols//2:]))
LS.append(ls)
# 重新构建图像
ls_ = LS[0]
for i in range(1,6):
ls_ = cv2.pyrUp(ls_)
ls_ = cv2.add(ls_, LS[i])
# 连接
real = np.hstack((A[:,:cols//2],B[:,cols//2:]))
cv2.imshow("apple",A)
cv2.imshow("orange",B)
cv2.imshow("LS",ls_)
cv2.imshow("Real",real)
cv2.waitKey()
cv2.destroyAllWindows()



![c++(空间配置器)[32]](https://img-blog.csdnimg.cn/72a245b93e5e42cf95e8193a1418640f.png)