前言

        递归就是每次执行方法调用都会先把当前的局部变量、参数值和返回地址等压入栈中，后面在递归返回的时候，从栈顶弹出上一层的各项参数继续执行，这就是递归为什么能够自动返回并执行上一层的方法的原因。因此，我们也可以模拟一个栈，将结果压入栈中，然后再从栈中弹出节点，就这样进行左右子树的遍历

迭代法实现前序遍历

前序遍历是中左右，如果还有左子树就一直向下找。完了之后再返回从最底层逐步向上向右找。 不难写出如下代码: (注意代码中，空节点不入栈) 

 代码实现

public List<Integer> preOrderTraverse(TreeNode root){
    List<Integer> res = new ArrayList<>();
    if(root == null){
        return res;
    }
    Deque<TreeNode> stack = new LinkedList<>();
    TreeNode temp = root;
    while(!stack.isEmpty() || temp != null){
        while(temp != null){
            res.add(temp.val);
            stack.push(temp);
            temp = temp.left;
        }
        temp = stack.pop();
        temp = temp.right;
    }
    return res;
}

 迭代法实现中序遍历

 代码实现

  /**
     * 迭代法  实现  中序遍历
     * @param root 根节点
     * @return 中序遍历的节点集合
     */
    public List<Integer> cenOrderTraverse(TreeNode root){
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        while ( root != null || ! stack.isEmpty()){
            while (root != null){
                stack.push(root);
                root = root.left;
            }
            root =  stack.pop();
            res.add(root.val);
            root = root.right;
        }
        return res;
    }

 迭代法实现后序遍历 

 实现要点

        后序遍历的非递归实现有三种基本的思路: 反转法、访问标记法、和Morris法可惜三种理解起来都有些难度，如果头发不够，可以等一等再学习。
        这里只介绍一种好理解又好实现的方法: 反转法

实现思路 

如下图，我们先观察后序遍历的结果是seg=9 5 7 4 3，如果我们将其整体反转的话就是new seq={3 4 7 5 9}

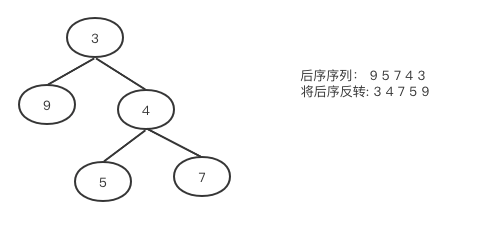
          要得到new seq的方法和前序遍历思路几乎一致，只不过是左右反了。前序是先中间，再左边然后右边，而这里是先中间，再后边然后左边。那我们完全可以改造一下前序遍历，在前序基础上修改左右孩子进入栈的顺序，即先遍历右孩子，将其压入栈，最后才遍历左孩子，得到序列new seq之后再通过Collections工具类的reverse()方法，再reverse一下就是想要的结果了，代码如下:

    /**
     * 反转法  实现  后序遍历
     * @param root 根节点
     * @return 后序遍历的节点集合
     */
    public List<Integer> postOrderTraverse(TreeNode root){
        ArrayList<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null){
            while (node != null){
                res.add(node.val);
                stack.push(node);
                node = node.right;
            }
            node = stack.pop();
            node = node.left;
        }
        Collections.reverse(res);
        return res;
    }