这篇文章向大家介绍一个因子分析的实践操作案例。

这篇文章使用的数据集来自于一份问卷，数据集包括31个题目，178个观测（因子分析对观测数有规定，一般要求观测的记录数为题目数量的5到10倍，至少5倍，此数据集的记录数基本满足要求），现在希望对此数据集进行因子分析，提取出几个因子，提取出因子后，需要对因子进行命名。

打开数据集什么的就不说了，操作过程也和前面介绍的主成分分析类似，本文我们主要来看一下如何提取合适的因子。

最开始，我们直接将需要分析的题目选入，点击【确定】，进行分析即可，此时可以输出检验是否可以进行因子分析的统计量，KMO统计量与球形检验。

 

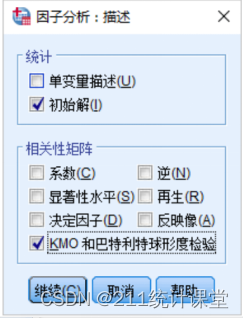
结果表明，KMO >0.9,球形检验也通过，适合做因子分析。

 

我们来看输出的总的方差解释这张表，注意看【累计的方差贡献率】，以及【总计】这两列，【总计】这列表示的是特征值，所谓特征值通俗的讲就是它代表相当于原来平均多少个题目，特征值小于1的因子代表性比不上原有的一个题目，所以软件默认只提取特征值大于1的因子。

 

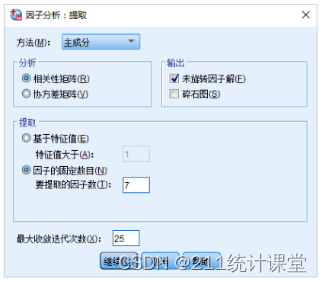
在我们做具体的分析时，还要结合因子的可解释性，累计方差贡献率来决定提取多少个因子，就本案例而言，如果只提取特征值大于1的因子，累计的方差贡献率才64%，有点低（一般达到80%以上为好）。而且第6,7因子的特征值很接近于1，如果有需要，其实我们可以把这两个因子也提取出来，也就是说我们可以提取7个因子。

在本案例中，如果我们提取5个因子，最终因子的结构不好解释，这个研究的初期，就确定，不应该少于6个因子，下图为最终得到的因子结构。

 

需要注意，一般情况下通过主成分方法提取的因子，都需要对因子进行旋转，最大方差法是正交旋转，这种旋转方法得到的因子之间没有相关关系，也可以采用斜交法进行旋转，通过斜交法旋转得到的因子之间可能具有相关关系。可以通过取消小系数，来查看因子的结构。

（选择旋转方法）

 

（不显示小系数，系数低于0.5的不显示，可自己进行尝试，直到每个题目前只有一个系数为准）

 

我们这里重新确定提取因子的数量为7，并利用方差最大法进行旋转，取消小系数，得到旋转后的成分矩阵，通过该表格，我们能够清晰看到因子的结构。

 

（成分矩阵，同一列中，显示有系数的变量可归为一个因子，每个因子的结构清晰可见）

 

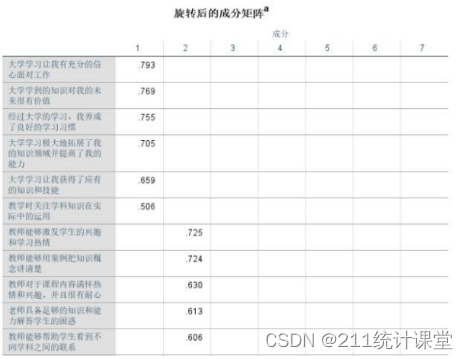
最后根据各组因子对应的题目，对各个因子进行命名，至此因子分析就结束了。不过因子分析一般作为中间过程，得到的分析结果一般还需要结合其它的统计分析方法使用