第十六次CCF计算机软件能力认证

第一题：小中大

在数据分析中，最小值最大值以及中位数是常用的统计信息。

老师给了你 n 个整数组成的测量数据，保证有序（可能为升序或降序)，可能存在重复的数据。

请统计出这组测量数据中的最大值、中位数以及最小值，并按照从大到小的顺序输出这三个数。

输入格式

第一行输入一个整数 n。

第二行中存在 n 个有序的整数，表示测量数据，可能为升序或降序排列，可能存在连续多个整数相等，整数与整数之间使用空格隔开。

输出格式

包含一行，包括最大值、中位数以及最小值共三个数，并按照从大到小的顺序输出。

数据与数据之间使用空格隔开。

对于整数请直接输出整数，对于可能出现的分数，请输出四舍五入保留 1 位小数的结果。

数据范围

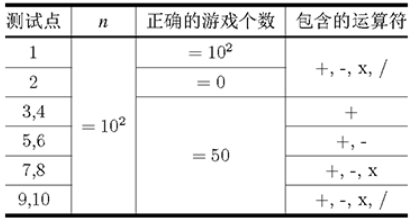
测试点 n 测量数据的绝对值测量数据是否均相同
1,2 ≤1e3 ≤1e7 是
3,4,5,6 ≤1e3 ≤1e7 否
7,8 ≤1e5 ≤1e7 是
9∼20 ≤1e5 ≤1e7 否

输入样例1：
3
-1 2 4
输出样例1：
4 2 -1
样例1解释

4 为最大值，2 为中位数，−1 为最小值。

输入样例2：
4
-2 -1 3 4
输出样例2：
4 1 -2
样例2解释

4 为最大值，(−1+3)÷2=1 为中位数，−2 为最小值。

测试点	n	测量数据的绝对值	测量数据是否均相同
1,2	≤1e3	≤1e7	是
3,4,5,6	≤1e3	≤1e7	否
7,8	≤1e5	≤1e7	是
9∼20	≤1e5	≤1e7	否

#include<iostream>

using namespace std;

const int N = 1e5 + 10;
int n;
int a[N];
int _max = -0x3f3f3f3f , _min = 0x3f3f3f3f;

int main()
{
    cin >> n;
    for(int i = 0;i < n;i ++) cin >> a[i] , _max = max(_max , a[i]) , _min = min(_min , a[i]);
    double x = 0;
    if(n & 1) x = a[n / 2];
    else x = (a[n / 2] + a[n / 2 - 1]) * 1.0 / 2;
    
    if((int)x == x)printf("%d %d %d" , _max , (int)x , _min);
    else printf("%d %.1lf %d" ,_max , x , _min);
    return 0;
}

n = int(input())
l = list(map(int , input().split()))
x = 0
if n & 1:
    x = l[n // 2]
else:
    x = (l[n // 2 - 1] + l[n // 2]) / 2
print(max(l) , end = ' ')
if int(x) == x:
    print(int(x) , end = ' ')
else:
    print("%.1lf" %(x) , end = ' ')
print(min(l))

第二题：二十四点

二十四点是一款著名的纸牌游戏，其游戏的目标是使用 3 个加减乘除运算使得 4 张纸牌上数字的运算结果为 24。

定义每一个游戏由 4 个从 1−9 的数字和 3 个四则运算符组成，保证四则运算符将数字两两隔开，不存在括号和其他字符，运算顺序按照四则运算顺序进行。

其中加法用符号 + 表示，减法用符号 - 表示，乘法用小写字母 x 表示，除法用符号 / 表示。

在游戏里除法为整除（向下取整），例如 2/3=0,3/2=1,4/2=2，−3/7=−1。

老师给了你 n 个游戏的解，请你编写程序验证每个游戏的结果是否为 24。

输入格式

第一行输入一个整数 n。

从第 2 行开始到第 n+1 行中，每一行包含一个长度为 7 的字符串，为上述的 24 点游戏，保证数据格式合法。

输出格式

包含 n 行，对于每一个游戏，如果其结果为 24 则输出字符串 Yes，否则输出字符串 No。

数据范围

输入样例：
10
9+3+4x3
5+4x5x5
7-9-9+8
5x6/5x4
3+5+7+9
1x1+9-9
1x9-5/9
8/5+6x9
6x7-3x6
6x4+4/5
输出样例：
Yes
No
No
Yes
Yes
No
No
No
Yes
Yes
样例解释
9+3+4×3=24
5+4×5×5=105
7-9-9+8=-3
5×6/5×4=24
3+5+7+9=24
1×1+9-9=1
1×9-5/9=9
8/5+6×9=55
6×7-3×6=24
6×4+4/5=24

解题思路：

使用python的eval函数进行求解

for _ in range(int(input())):
    s = input()
    s = s.replace("x" , "*")
    s = s.replace("/" , "//")
    if eval(s) == 24:
        print("Yes")
    else:
        print("No")

第三题：损坏的RAID5（这一次的最难的）

大模拟

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef unsigned int UI;
const int N = 1010, M = 40 * 1024 * 8 + 10;

int n, s, l;
UI disk[N][M / 8];
bool st[N];
char str[M];
int len;

inline UI get(char c)
{
    if (c <= '9') return c - '0';
    return c - 'A' + 10;
}

inline char get(UI x)
{
    if (x <= 9) return x + '0';
    return x - 10 + 'A';
}

inline string u2s(UI x)
{
    string res;
    for (int i = 7; i >= 0; i -- )
        res += get(x >> (i << 2) & 15);
    return res;
}

inline int get_real_col(int r, int c)
{
    r %= n;
    r = n - 1 - r;
    return (r + 1 + c) % n;
}

int main()
{
    scanf("%d%d%d", &n, &s, &l);
    for (int u = 0; u < l; u ++ )
    {
        int k;
        scanf("%d", &k);
        getchar();
        fgets(str, M, stdin);
        int sz = strlen(str) - 1;
        for (int i = 0; i < sz; i += 8)
        {
            UI x = 0;
            for (int j = 0; j < 8; j ++ )
                x = (x << 4) + get(str[i + j]);
            disk[k][i >> 3] = x;
        }
        st[k] = true;
        len = max(len, sz >> 3);
    }

    int m;
    scanf("%d", &m);
    while (m -- )
    {
        int b;
        scanf("%d", &b);
        if (b >= len * (n - 1)) puts("-");
        else
        {
            int k = b / s;
            int row = k / (n - 1), col = get_real_col(row, k % (n - 1));
            int r = row * s + b % s;
            if (st[col])
                puts(u2s(disk[col][r]).c_str());
            else if (l == n - 1)
            {
                UI x = 0;
                for (int i = 0; i < n; i ++ ) x ^= disk[i][r];
                puts(u2s(x).c_str());
            }
            else puts("-");
        }
    }
    return 0;
}。

第四题：消息传递接口

解题思路：使用队列进行模拟，信息传递接口

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <sstream>

using namespace std;

const int N = 10010;

int n;
struct Op
{
    // 0代表S 1代表R -1代表等待
    int p, id;
};
queue<Op> q[N];
bool st[N];// 判断该进程是否在等待

// 功能: PD pid进程当前指令能否执行完毕, 目前pid执行到{!type, oid}, 即期望对方是type
bool dfs(int p, int id, int pid)
{
    // 若等待的对方也在等待，则死锁
    if (st[id]) return false;
    st[id] = true;
    
    // 对方进入等待队列
    while (q[id].size())
    {
        auto t = q[id].front();
        
         // 如果对方等的那个刚刚好是自己，且刚刚好是自己所期待的
        if (t.p == p && t.id == pid)
        {
            st[id] = false;
            q[id].pop();
            return true;
        }
        // PD 对方当前指令能否完成
        else if (dfs(t.p ^ 1, t.id, id)) q[id].pop();
        else return false;
    }
    st[id] = false;
    return p == -1;
}

int main()
{
    int T;
    cin >> T >> n;
    getchar();
    while (T -- )
    {
        string str;
        for (int i = 0; i < n; i ++ )
        {
            st[i] = false;
            q[i] = queue<Op>();
            getline(cin, str);
            stringstream ssin(str);
            while (ssin >> str)
                if (str[0] == 'S') q[i].push({0, stoi(str.substr(1))});
                else q[i].push({1, stoi(str.substr(1))});
        }

        // 添加一个-1进程，等待所有0~n-1进程执行完
        bool success = true;
        for (int i = 0; i < n; i ++ )
            if (!dfs(-1, i, -1))
            {
                success = false;
                break;
            }
        if (success) puts("0");
        else puts("1");
    }
    return 0;
}

第五题：317号子问题

经典的图论问题（SPFA 或迪杰斯特拉）

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>

using namespace std;
const int N = 1e4 + 10 , M = 2e5 + 10 , INF = 0x3f3f3f3f;
typedef pair<int , int>PII;
int h[M] , ne[M] , w[M] , e[M] , idx;

void add(int a , int b , int c)
{
    e[idx] = b , w[idx] = c , ne[idx] = h[a] , h[a] = idx ++;
}
int solor[N];
int n , m , k;
bool st[N];
int dist[N] , cnt = 0;
int d[N][1010];

void dij(int s)
{
    memset(dist , 0x3f , sizeof dist);
    memset(st , 0 , sizeof st);
    dist[s] = 0;
    priority_queue<PII , vector<PII> , greater<PII>>q;
    q.push({0 , s});
    
    while(!q.empty())
    {
        auto t = q.top();
        q.pop();
        
        int x = t.second;
        if(st[x]) continue;
        st[x] = true;
        
        for(int i = h[x];~i;i = ne[i])
        {
            int j = e[i];
            if(dist[j] > dist[x] + w[i])
            {
                dist[j] = dist[x] + w[i];
                q.push({dist[j] , j});
            }
        }
    }
    
    for (int i = 1; i <= n; i ++ ) d[i][cnt] = dist[i];
}

void spfa(int start)
{
    int hh = 0, tt = 1;
    memset(dist, 0x3f, sizeof dist);
    int q[N];
    q[0] = start, dist[start] = 0;
    while (hh != tt)
    {
        int t = q[hh ++ ];
        if (hh == N) hh = 0;
        st[t] = false;

        for (int i = h[t]; ~i; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                if (!st[j])
                {
                    q[tt ++ ] = j;
                    if (tt == N) tt = 0;
                    st[j] = true;
                }
            }
        }
    }

    for (int i = 1; i <= n; i ++ ) d[i][cnt] = dist[i];
}

int main()
{
    memset(h , -1 , sizeof h);
    scanf("%d %d %d" ,&n ,&m ,&k);
    
    for(int i = 1;i <= n;i ++)
        scanf("%d" ,&solor[i]);
        
    while(m --)
    {
        int a , b , c;
        scanf("%d %d %d" ,&a ,&b ,&c);
        add(a , b , c) , add(b , a , c);
    }
    
    for(int i = 1;i <= n;i ++)
        if(solor[i])
        {
            // dij(i);
            spfa(i);
            cnt ++;
        }
    
    for(int i = 1;i <= n;i ++)
    {
        sort(d[i] , d[i] + cnt);
        int res = 0;
        
        for(int j = 0;j < cnt && j < k;j ++)
            if(d[i][j] != INF) res += d[i][j];
            else break;
        
        printf("%d\n" , res);
    }
    return 0;
}