一. 定义

1. 离散型随机变量的期望

2. 连续型随机变量的期望

定义2：设连续型随机变量 X的概率密度为f(x),  若积分 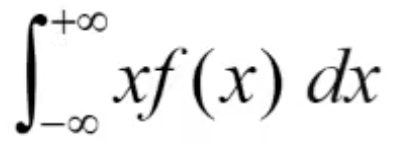 绝对收敛， 称其为X的数学期望。记为：  

注意： 被积函数是： xf(x)

看例题:

 

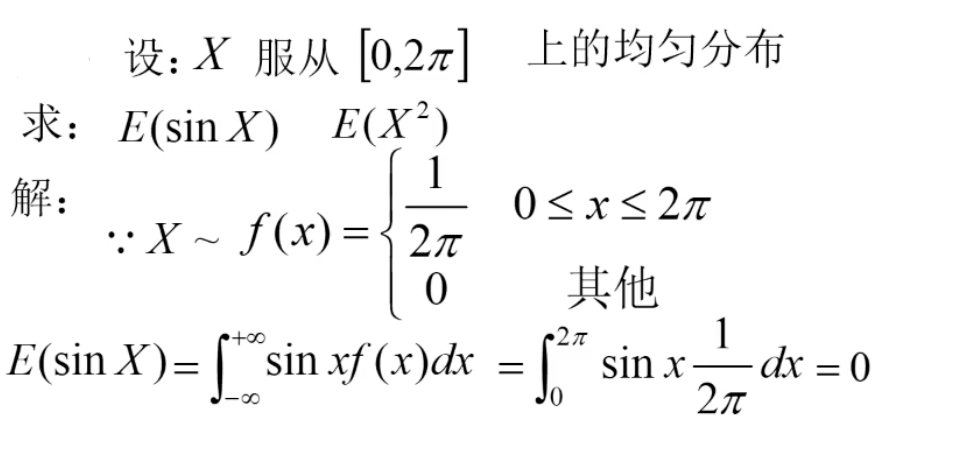
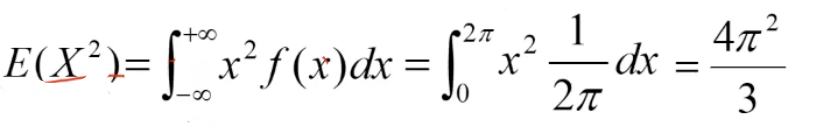
几种重要分布的数学期望参考 概率论_第4章__几种重要的随机变量的分布及其数字特征的表

3. 随机变量函数的期望

二  期望的性质

以下公式中C为常数,  X、Y为随机变量

1. E(C) = C

2. E(CX) = C·E(X)

3. E(X+Y) = E(X) + E(Y),   

上述可以推广为多个随机变量相加；

可以推广： E(C₁X+C₂Y) =  C₁E(X)+C₂E(Y)， 其中  C₁,  C₂为常数

4. 若X, Y是相互独立的随机变量，则  E(XY) = E(X)E(Y).