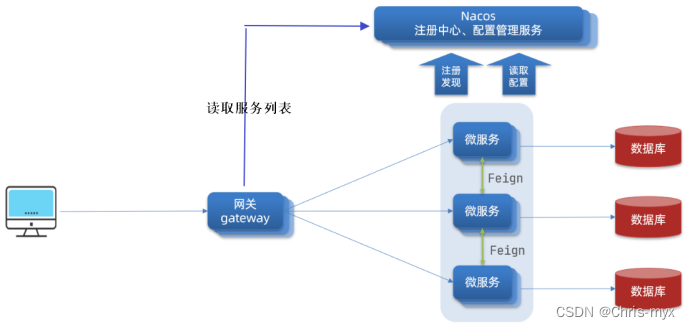
在七月算法上报了《无人驾驶实战》课程,老师讲的真好。好记性不如烂笔头,记录一下学习内容。 课程入口,感兴趣的也可以跟着学一下。
—————————————————————————————————————————
Planning是目前无人车最困难最有挑战性的部分

本质为一个优化问题,通过当前环境和当前状态,从现有可行的决策中,找到一个最优结果。
运动规划的三个领域:
机器人学:生成轨迹实现目标,有RRT,A*,D*和D* Lite等方法;控制论:动态系统理论实现目标状态,有MPC和LQR等方法;人工智能:生成状态和Action的一个映射,有Reinforcement Learning和Limitation Learning等方法;
如何解决一个运动规划问题:
将问题简化为一个简单的问题:路径寻找问题。什么样的路径是最好的,这个是需要用数字进行量化。常用的图论中的方法包括BFS、DFS和Dijkstra等。机器人学常用的方法为A* search,是基于Dijkstra方法的改进,前提是大概知道了终点位置,有个启发式的函数。
无人车中的规划和A* search相差多远。
无人车的特点是:部分感知,动态障碍物和复杂的环境。
而A* search本身是一个Global Algorithm。
局部观测的解决方法
使用贪心算法,使每一步在当前是最优的。

这里常用的方法为D* 方法。通过部分环境信息做出一个search,Apollo登月小车就是用的D*算法,而D* Lite是D*的一个简化版。
这种贪心算法一般很难得到全局最后解,但是也满足了当前的需求。
无人车路径规划的步骤
1.通过目标函数并且结合了平滑性和目标Cost;2.使用通用的search方法来最小化cost从而找到一个最优解;3.通过Partial observed information来做局部Planning;
如何设计出一个合理的轨迹
路径path+速度speed
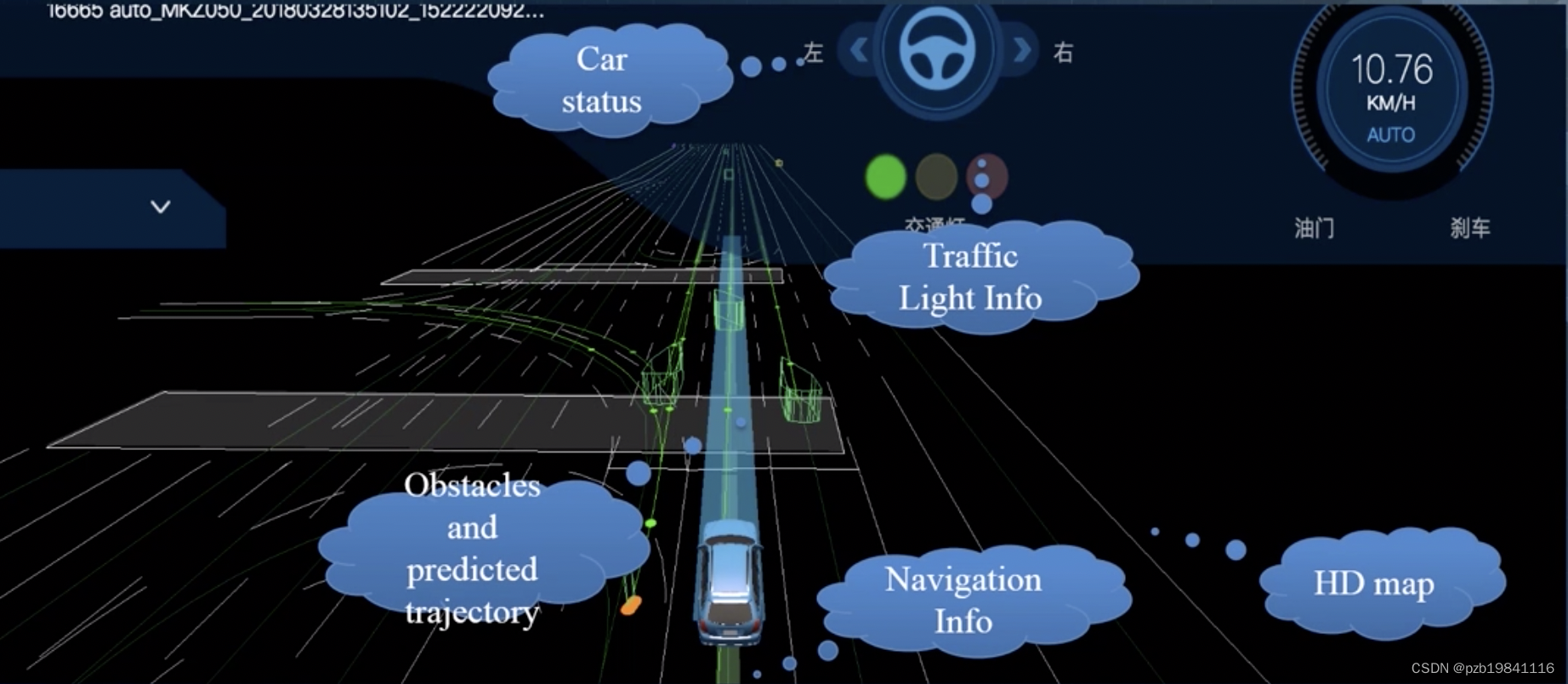
基本Planning方法
基于经典环境建模的方法:RRT和Lattice
现代无人车Planning方法:Darpa、Lattice in Frenet Frame和Spiral polynomial。
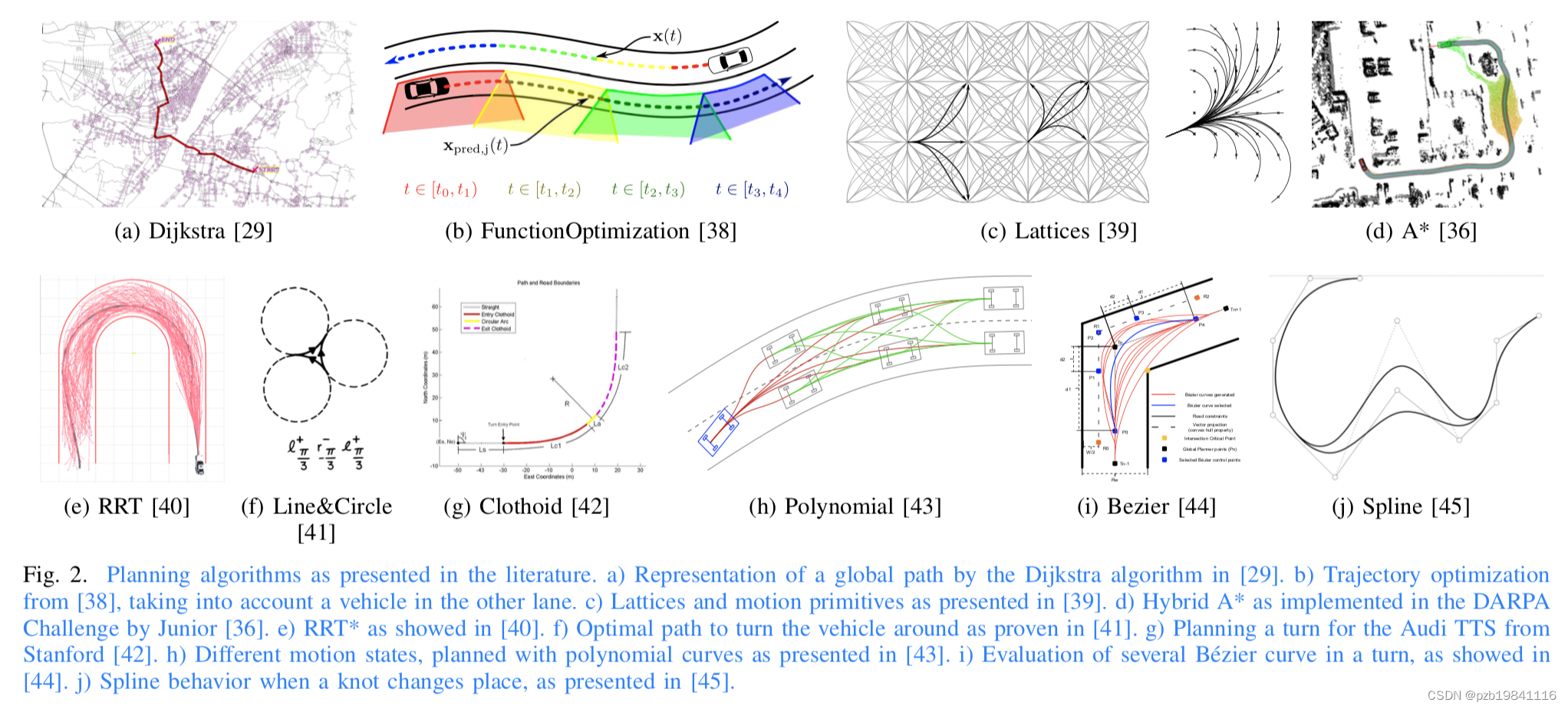
传统的机器人基础
PRM(Probabilistic RoadMap Planning)
非常常用的一个方法,先将连续空间离散化(随机撒点,Obstacle上的点删除),连接可行点,形成可行空间。最后通过A*算法找到最优路径。
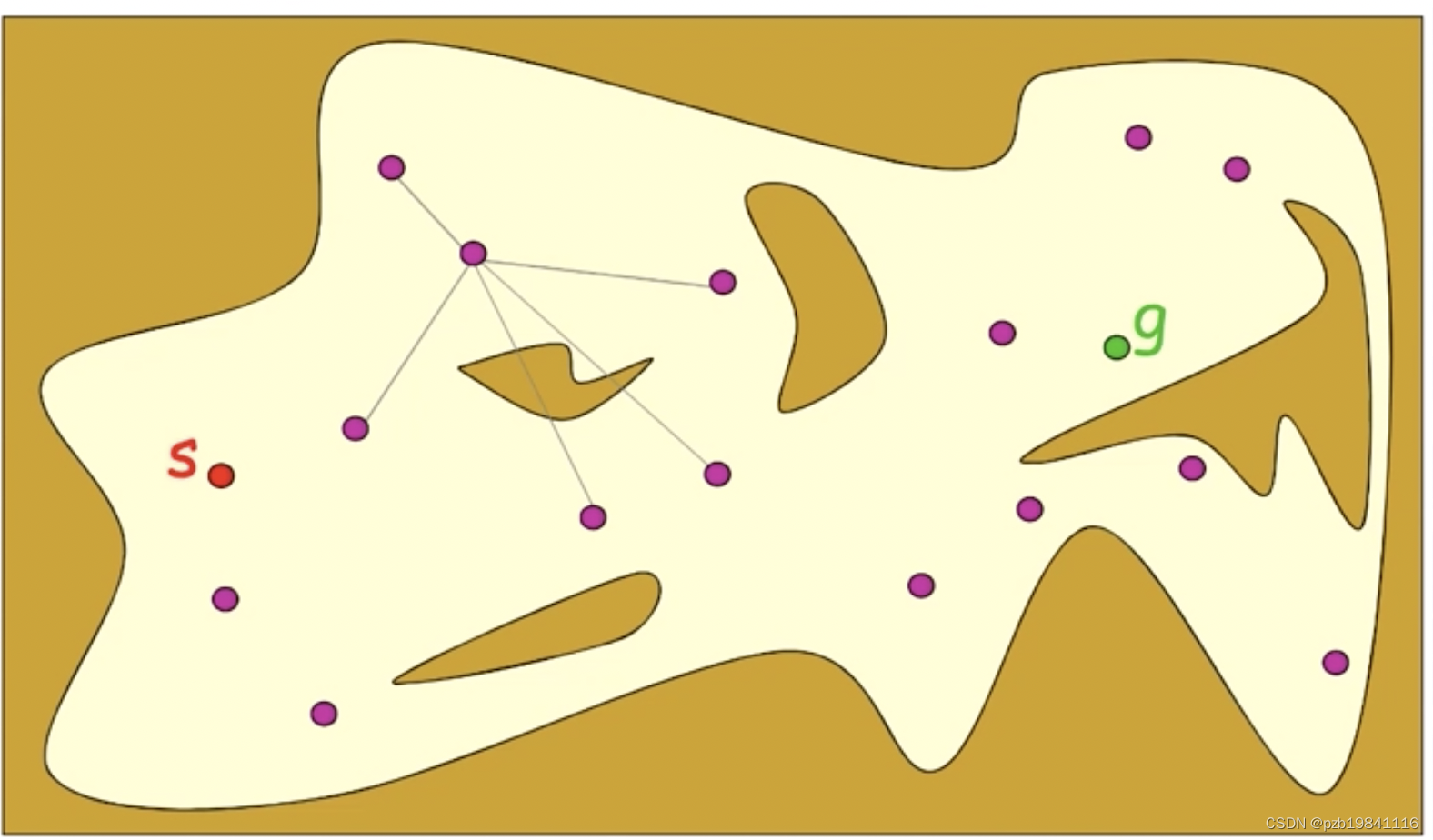
RRT(Incremental version of PRM)
使用增量搜索的方式来进行。

寻找附近可行点的最优点(F(x)最小,走过程中不能有阻碍)
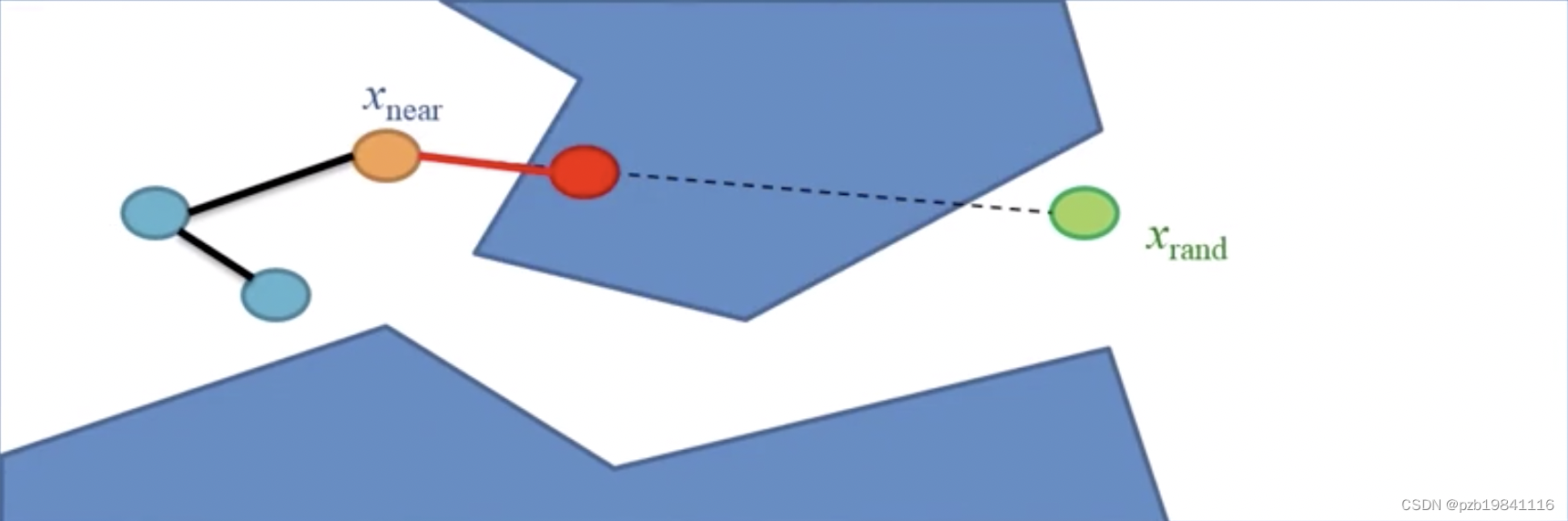
撒点搜索距离不能太远,一步一步移动。
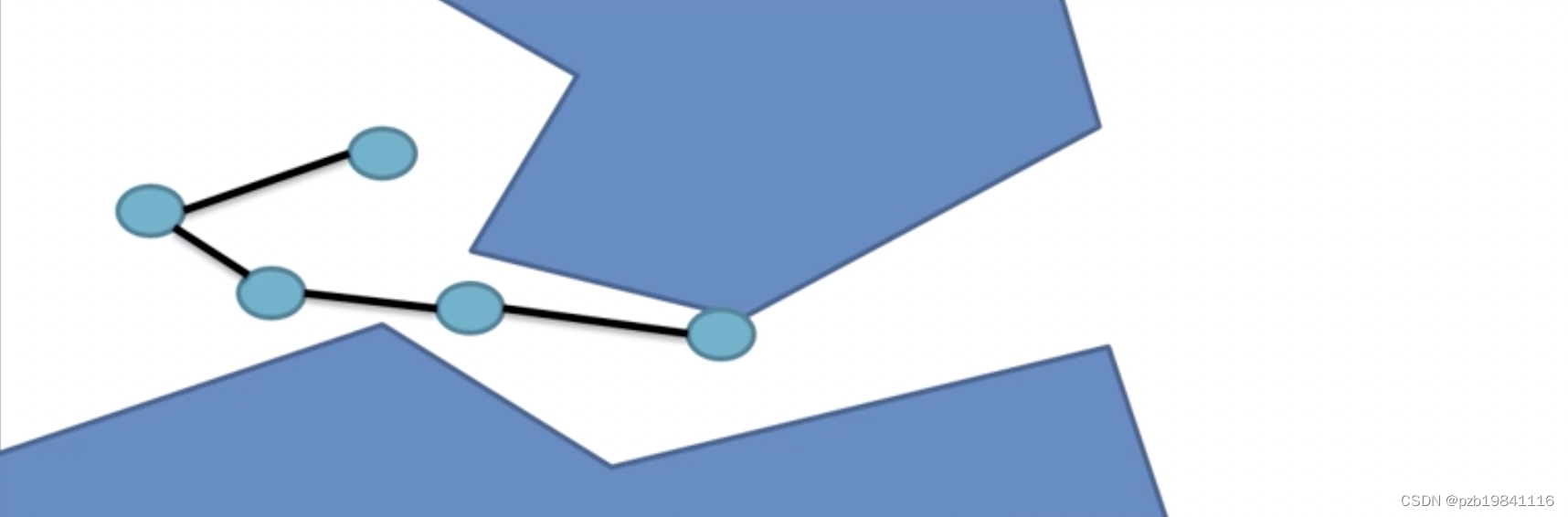
Lattice方法
改进了RRT的折线问题,给出了Path的平滑曲线,方法是网格化,每个采样格中都是用曲线连接。
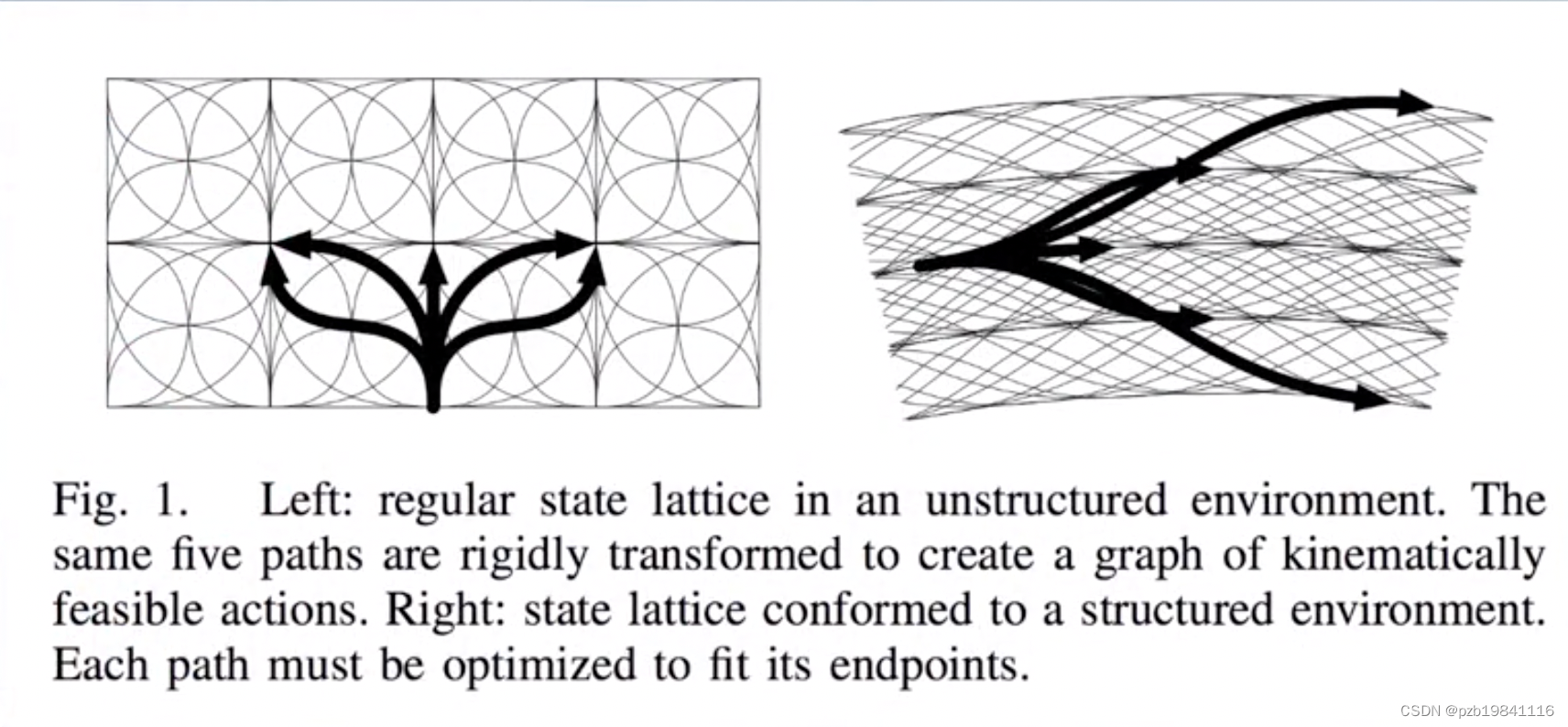
问题是该方式是个指数级别的搜索方法(NP-Hard)
DP(动态规划)
减少搜索空间,复用已有结果。

Lattice DP的平滑度够吗?曲率连续,但是曲率的导数不一定连续;
QP(二次规划)
凸优化问题最优化求解
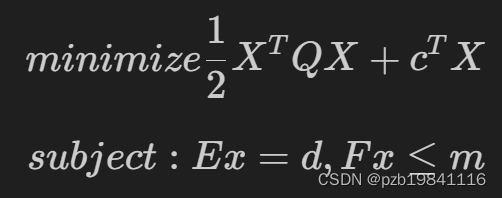
在凸优化中的凸空间问题,用QP有最优解。QP如何找到平滑曲线

其他的平滑曲线还有贝塞尔曲线、样条差值方法。
刚体模型;
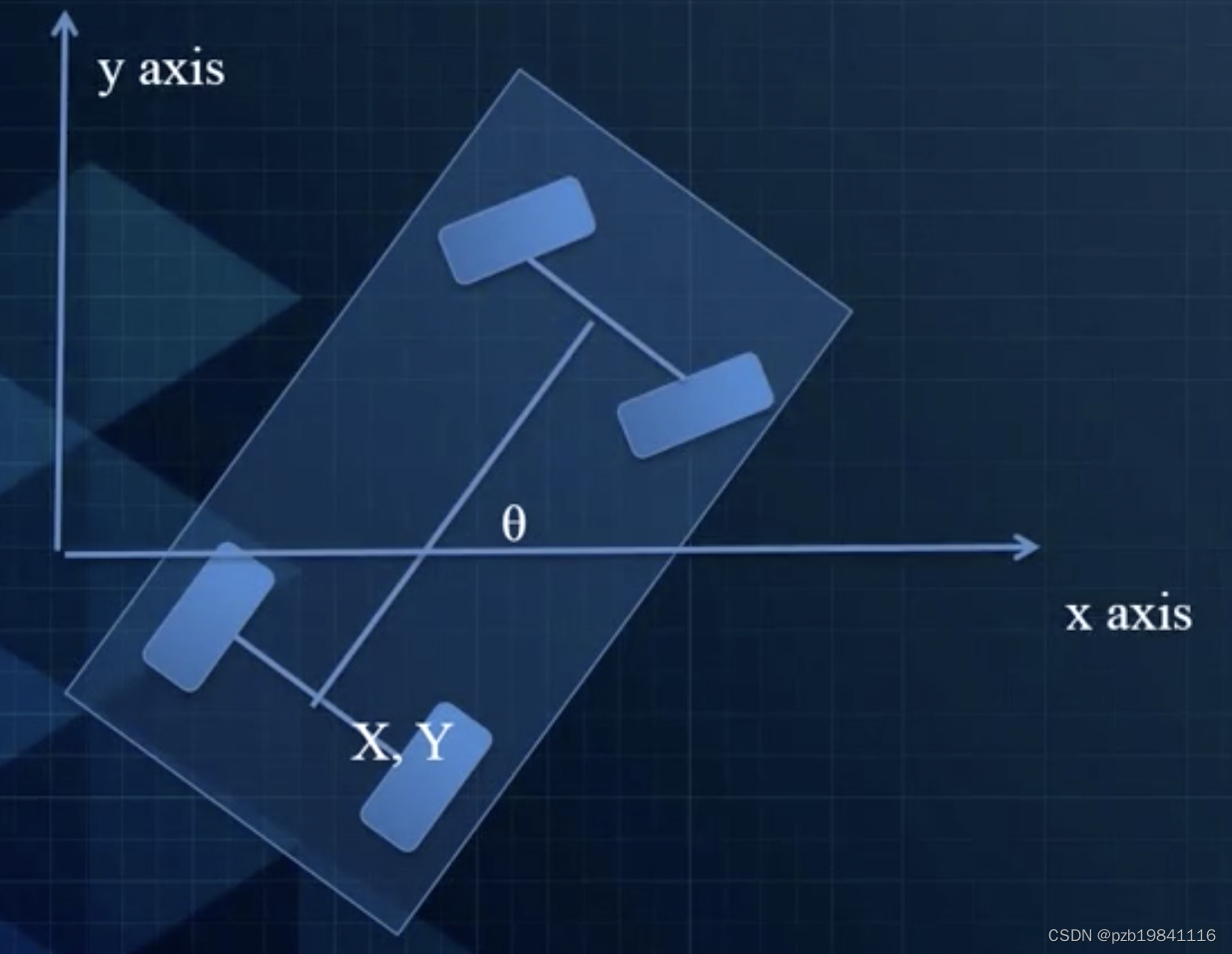
前轮转向和Heading的关系:车轮是沿着切线方向行驶;前后轮是同一个旋转中心;左右轮的结构相同。
Bicycle Model,是对汽车模型的一个简化,因为左右轮的结构是一样的。
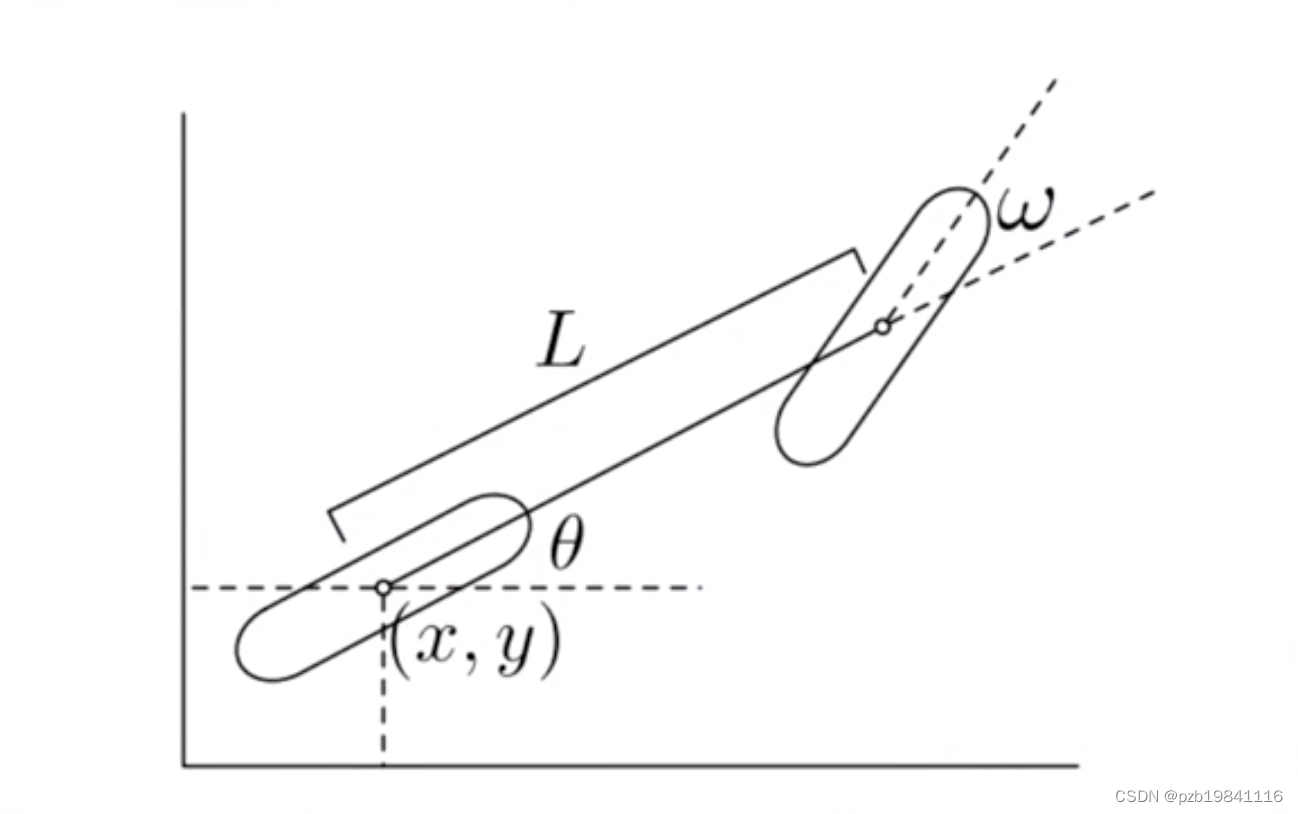
曲率公式为
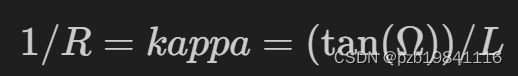
无人车Planning
从A点到B点,构建一个车辆运动轨迹,结合HD Map, Localization和Prediction。
输出:可行驶轨迹,有一系列点组成;包含两个层面:导航层面和运动轨迹层面
Routing(路由):导航一条A到B的全局路径。
输入:地图(路网信息,交通状态),当前位置,目的地(乘客决定)输出:可行驶道路的连接线搜索:地图数据转化成图网络,节点表示道路,边表示道路连接。
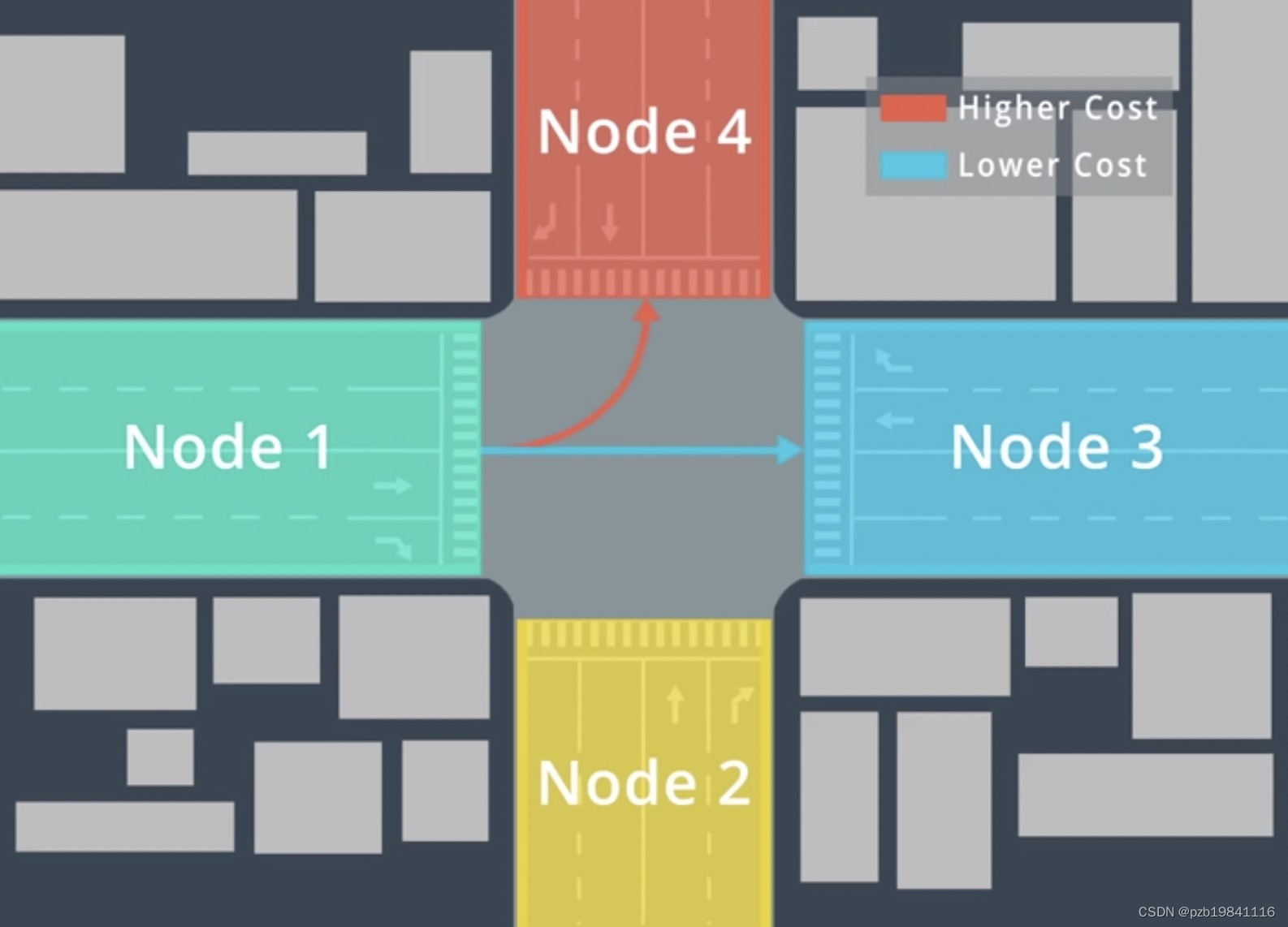
A*经典算法:
最经典的路径查找算法:F(n)=G(n)+H(n)
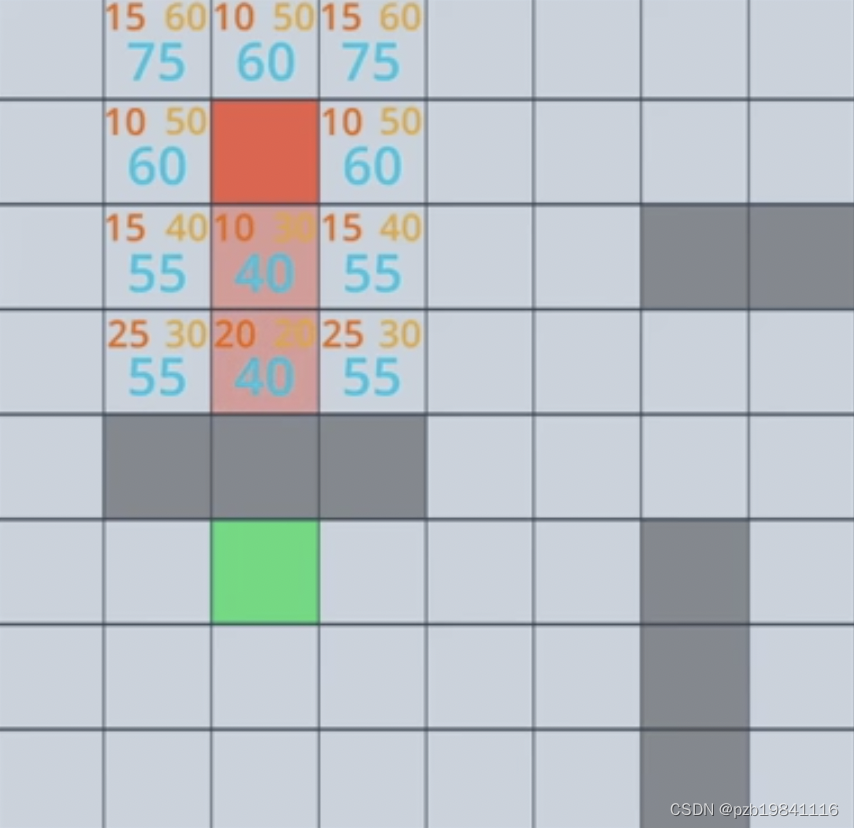
Fn表示道路的Routing的总cost,Gn表示起始点到候选点的Cost,Hn表示候选点通过启发式函数得到的目标点Cost
Motion Planning
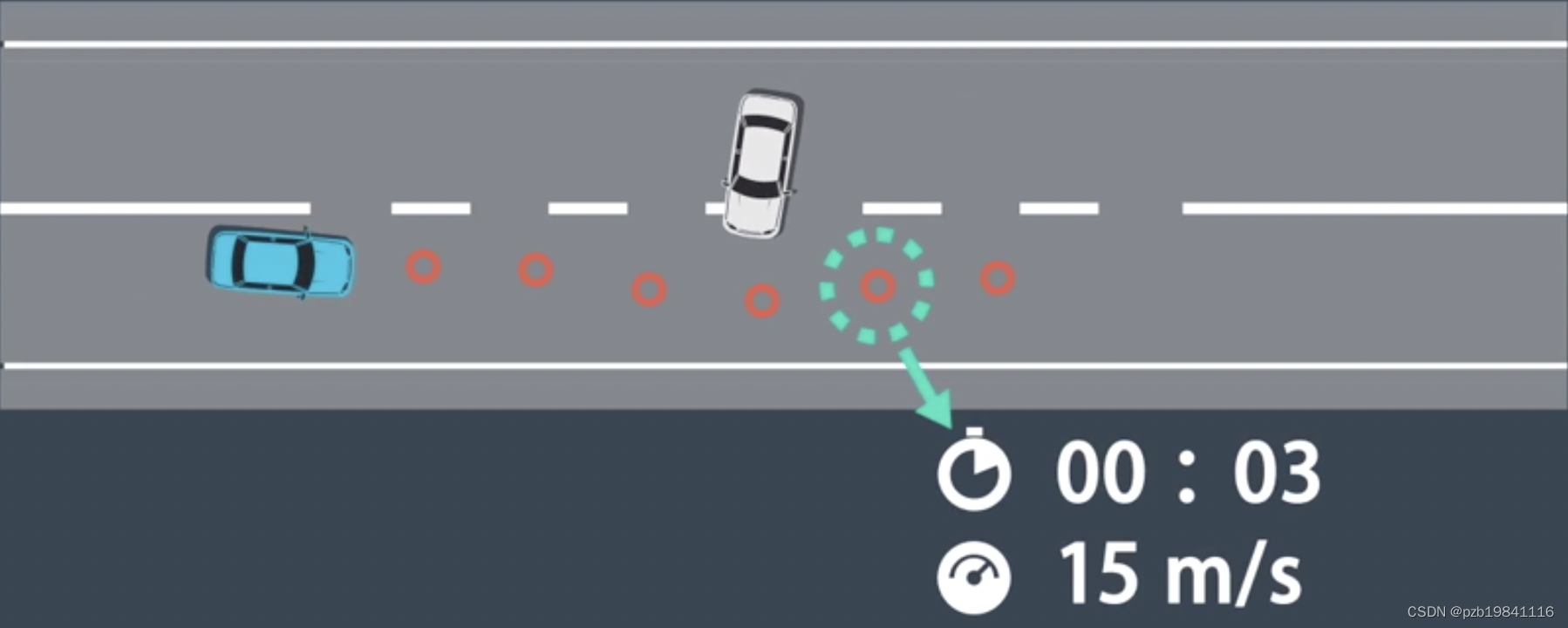
Planning理解为高精度、低级别的一个Search,trajectory Planning。轨迹点包含XY,Time和Velocity
规划的约束条件:碰撞、舒适、运动学约束、合法。
Cost Function 成本函数
由许多条件组成:道路偏离中心线距离,碰撞或者靠得太近,速度太快,Curvature太大
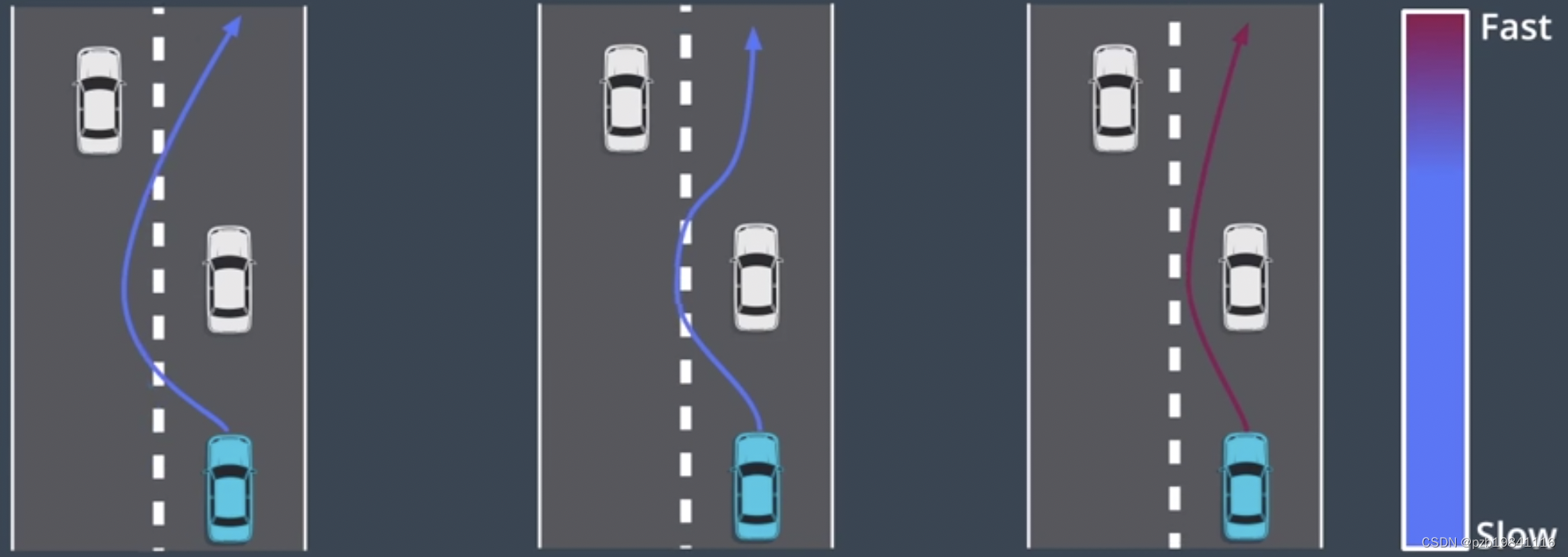

不同场景可能有不同的Cost Function:高速场景、停车场、不同车辆。
Frenet坐标系(车道坐标系)
笛卡尔坐标系的问题:xy坐标无法知道车开了多远,有没有偏离中心线,道路在哪里。
Frenet是基于Lane级别的,S表示走了多远,L表示距离车道有多偏。

Path与Speed解耦
Path Planning生成可行轨迹路径,Cost是平滑性、安全性及道路中心偏移距离。Speed Planning在每个Path上选择一系列速度,生成速度轨迹。
Path Planning
现生成道路网格(GridMap),每个网格单元中随机采样(撒点),每个网格选一个点,组成多条候选Path

Cost Function对这些轨迹进行评估,考虑中心线距离、障碍物距离、速度变化率和曲率等。
Speed Planning
主要是ST图,S表示Path上纵向距离,T表示运动时间。
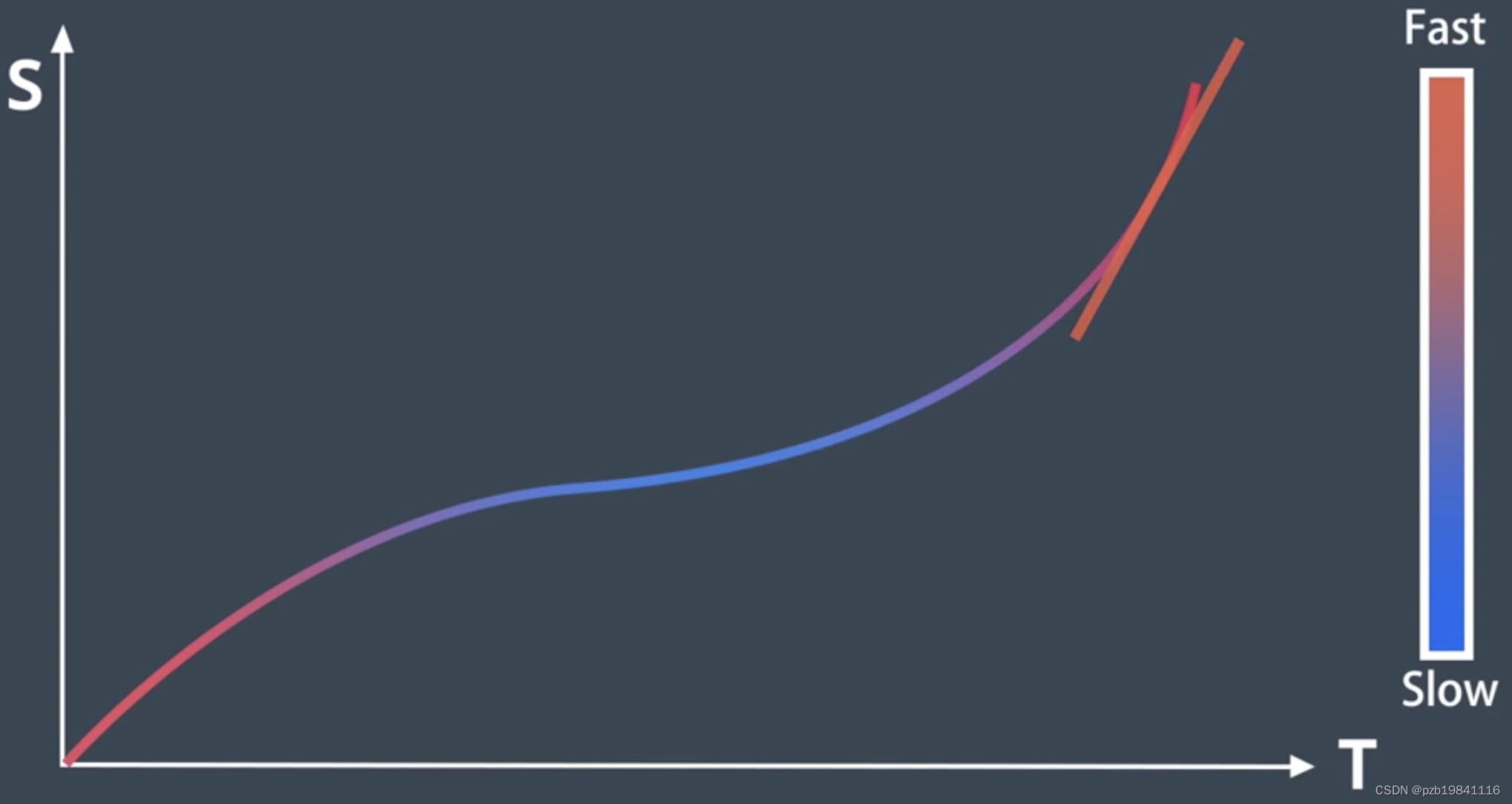
如何规划ST轨迹
1.连续空间离散化,单元格内速度保持不变

把障碍物投影进来,挡住我们Path轨迹的部分画进ST图中,因此必须要有良好的预测轨迹
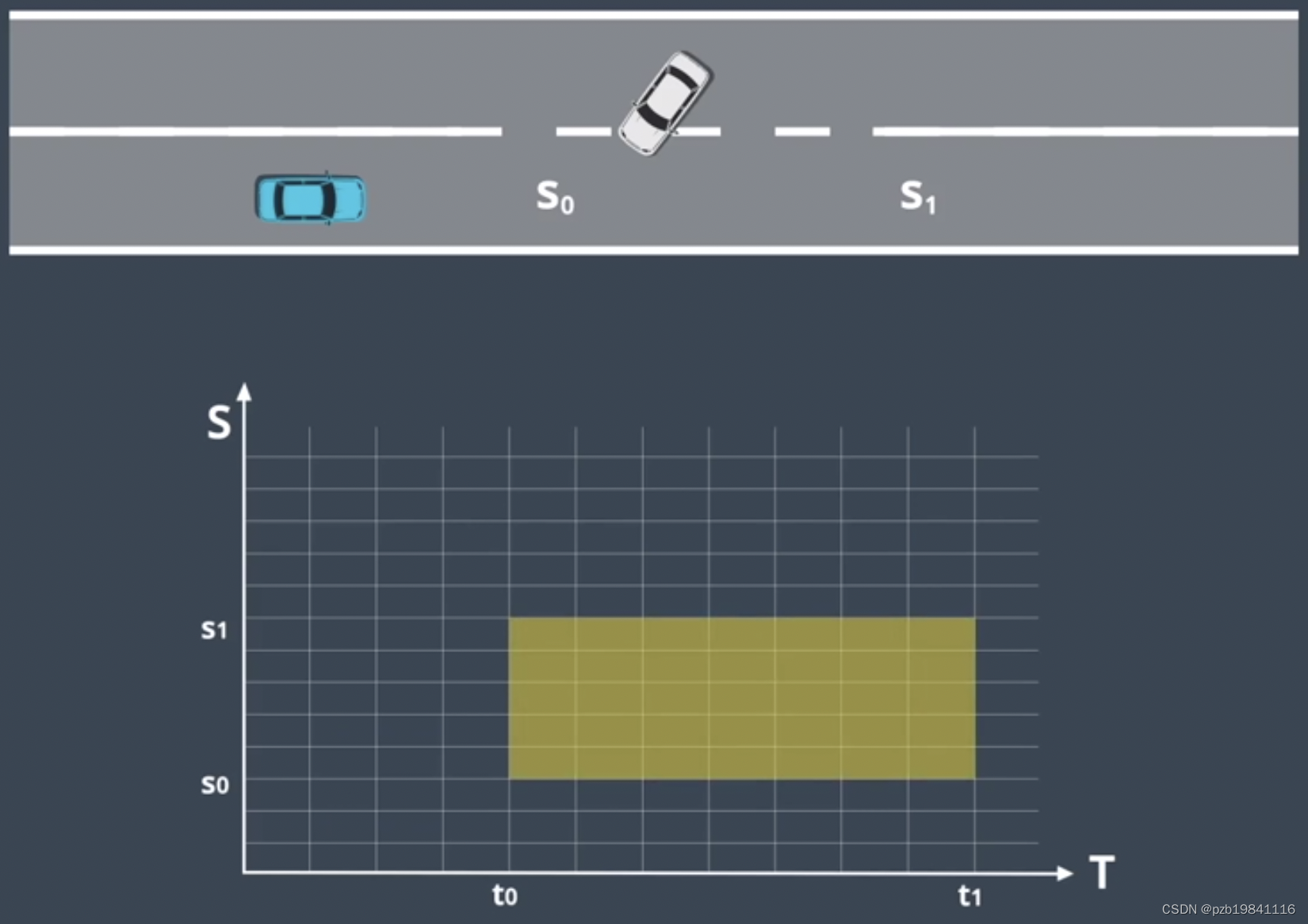
速度忑不能碰这个区域

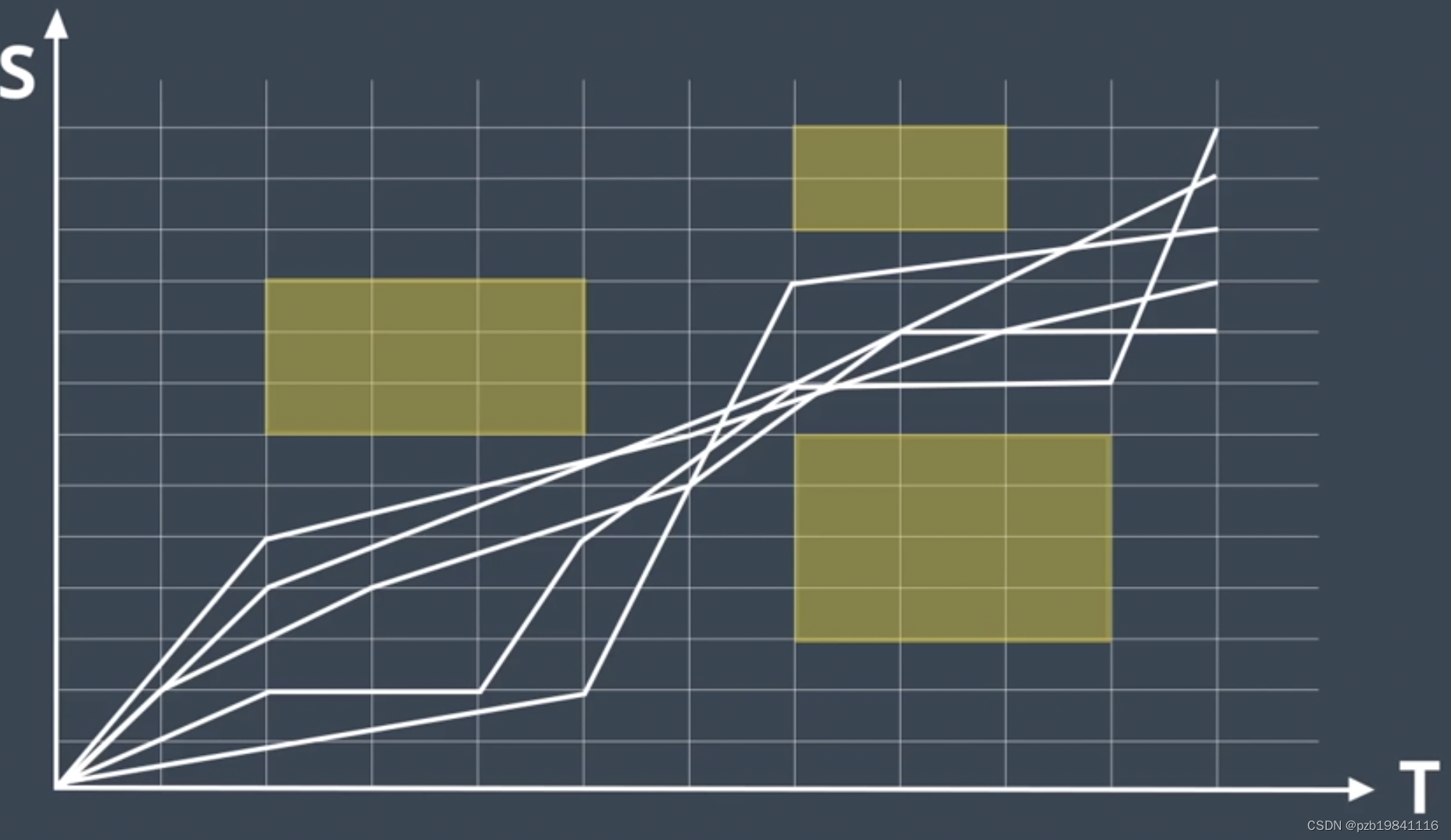
凸优化来求解得到的最优的速度曲线
限制条件:速度限制、距离限制、车辆运动学限制
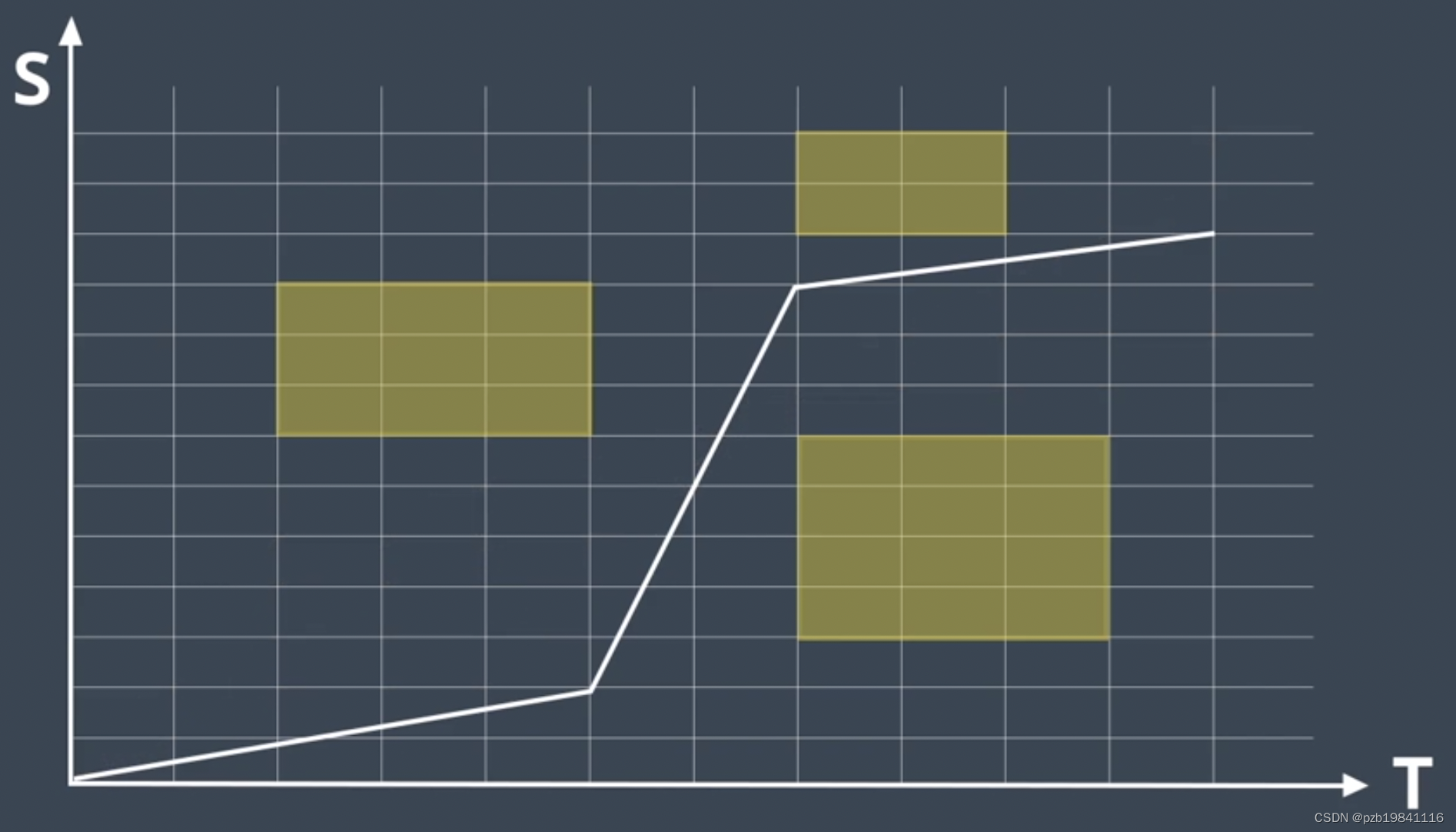
如何优化:对不平滑的速度线优化(QP)
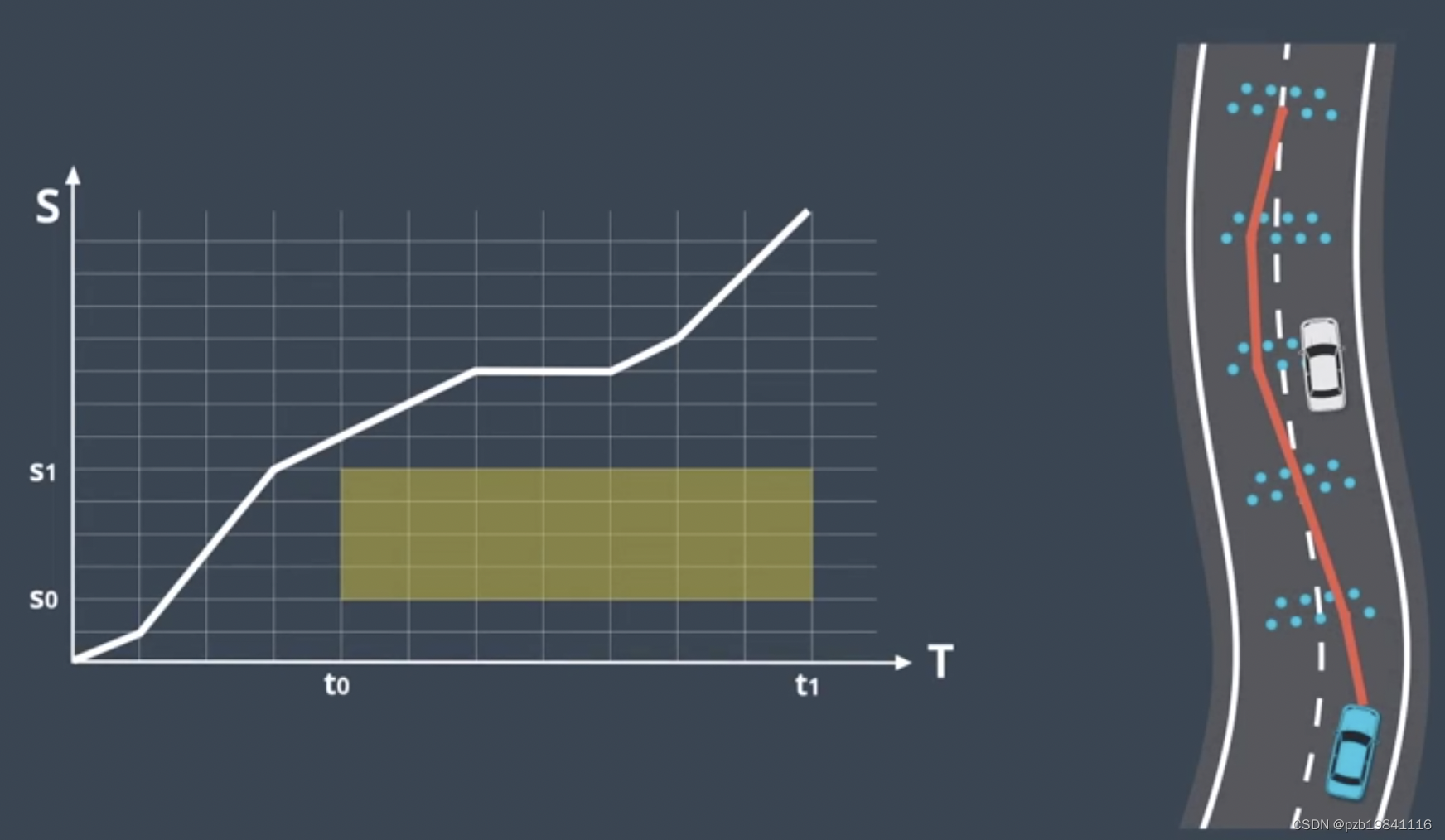
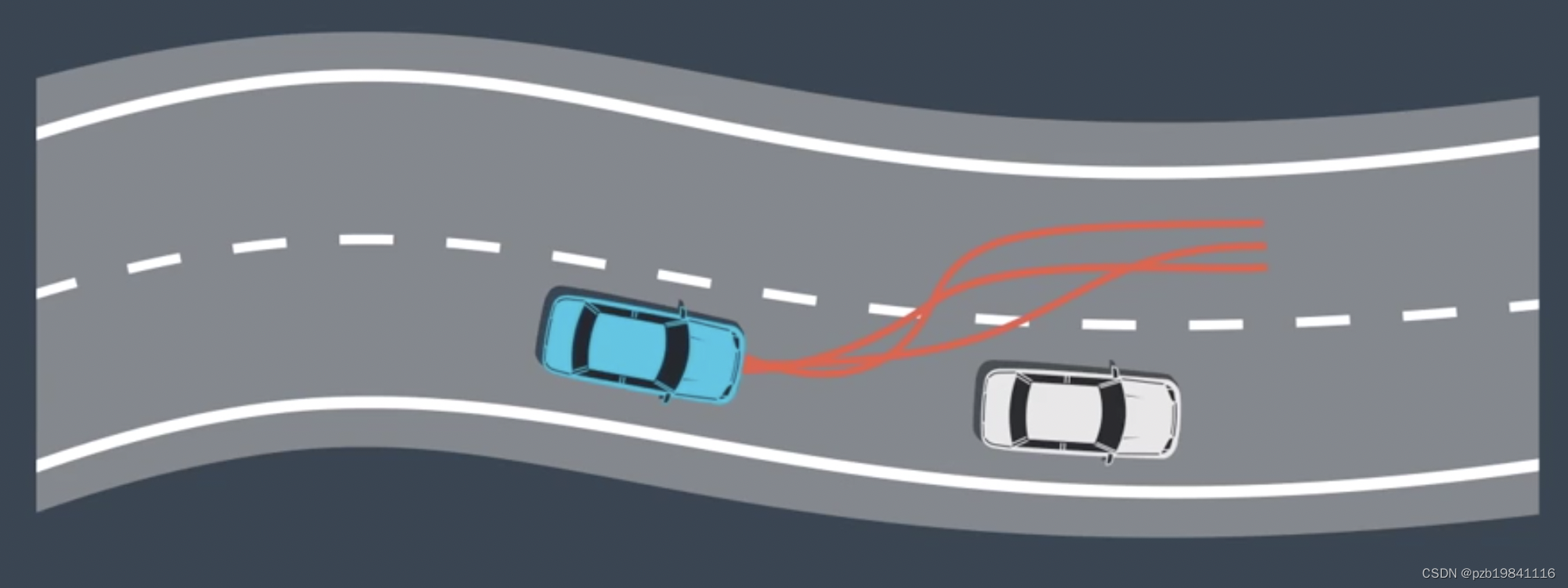
轨迹规划:遇到一辆很闷的车如何超车
1.生成很多轨迹线(撒点采样)
2.Cost Function对其进行评估,选择Cost最小的一条
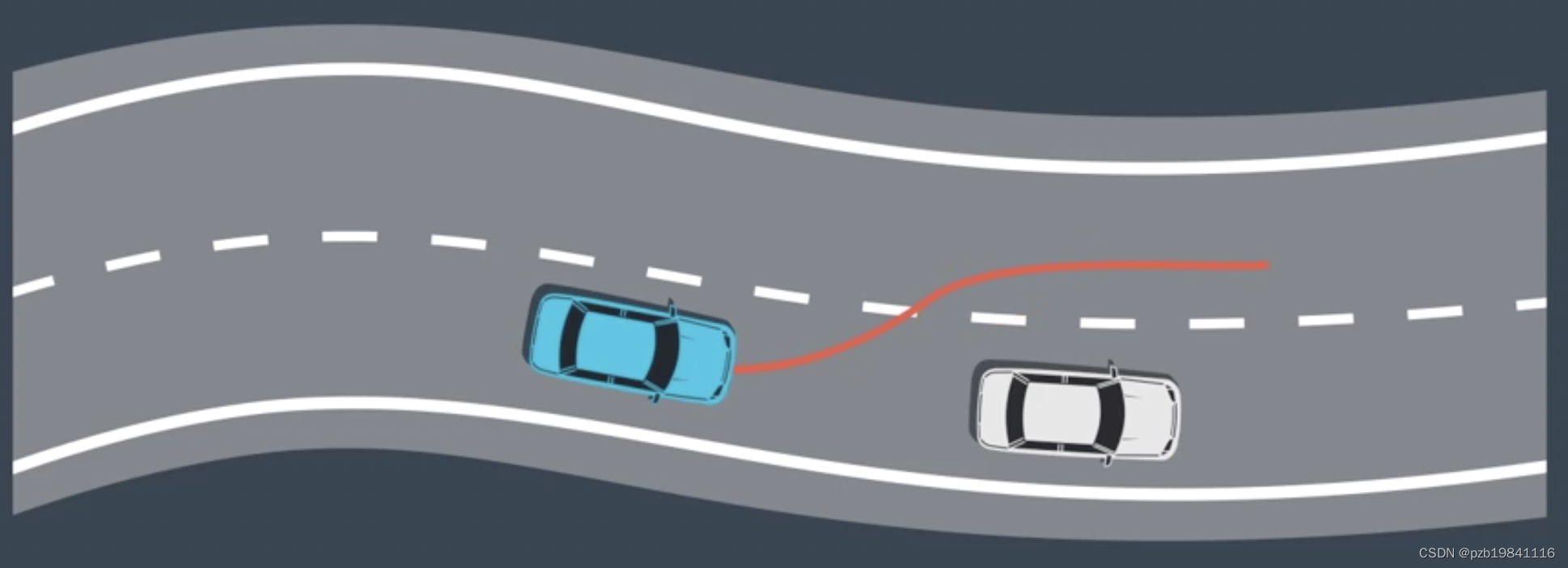
3.生成一个ST图来表示速度规划,生成多条速度曲线
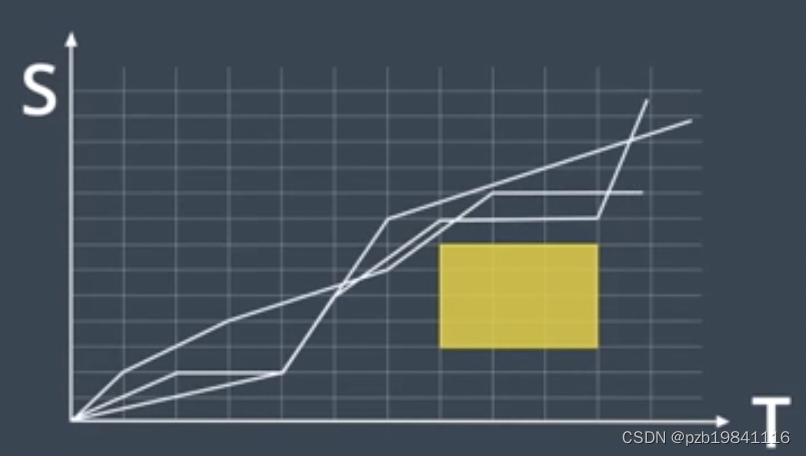
4.使用优化工具对多条速度采样进行最优化求解,让整个线路和速度曲线变得平滑
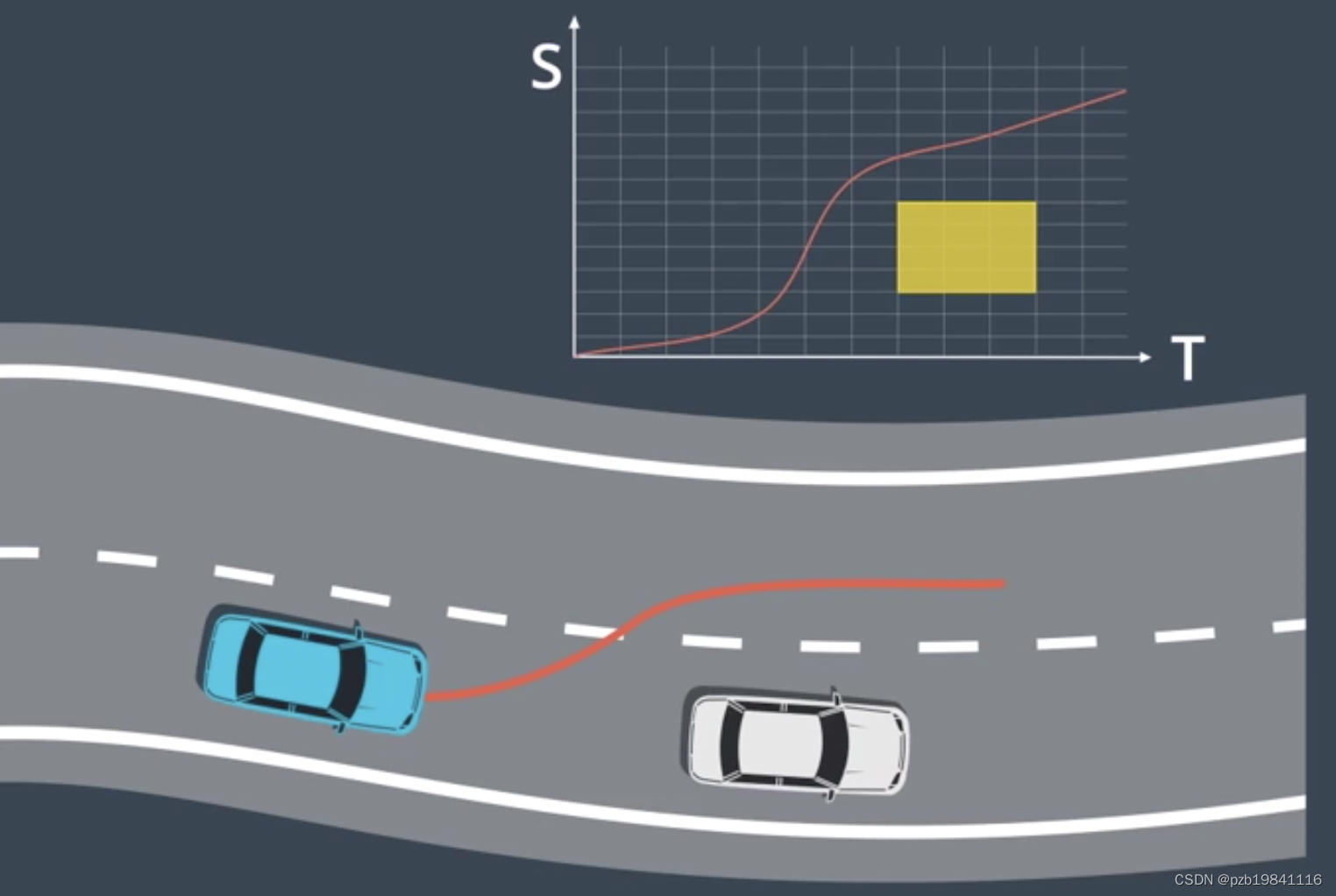
5.最后将每个轨迹点的Path和Speed合并得到最终结果

Lattice Planning(网格规划)
SL轨迹和ST轨迹
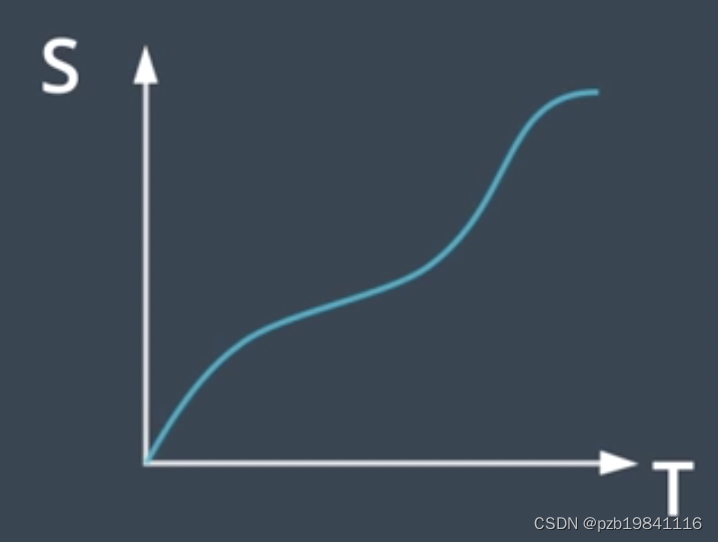
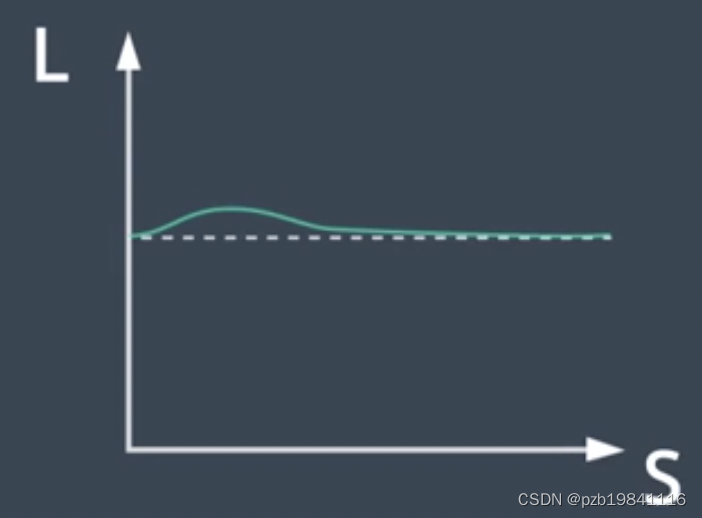
Lattice将两个图合并处理,同时进行Path和Speed的采样。
Lattice因为其采样计算量达,为了优化其采样效果,需要先进行场景化以简化计算量。S方向的优化,可根据特殊场景进行简化,比如定速巡航、跟随和停止等,都可以进行简化。L方向上的优化,需要保证车辆以一个稳定的状态进行重点状态,比如与车道线保持平齐。
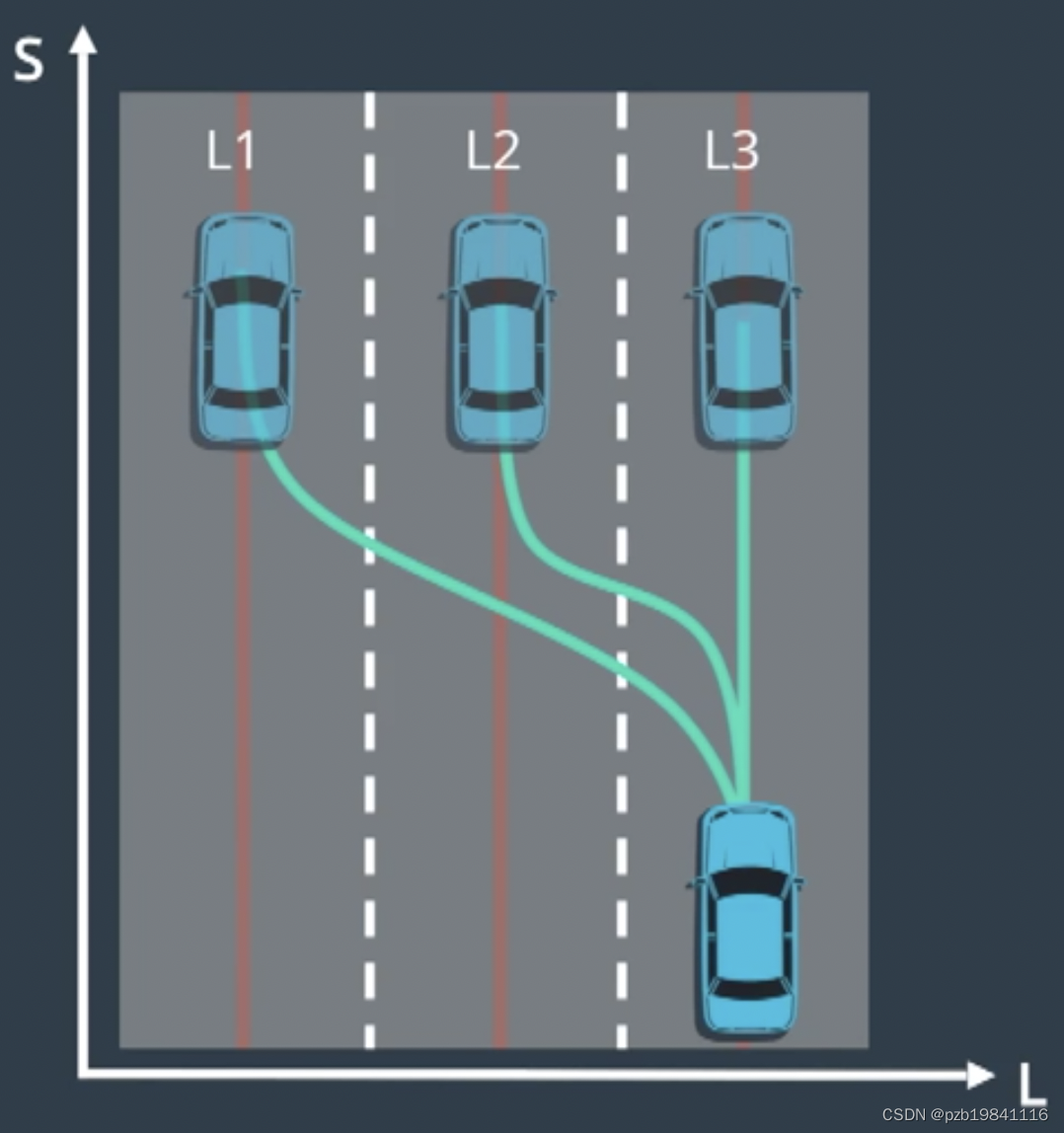
合并ST和SL的坐标
转化到笛卡尔坐标系下
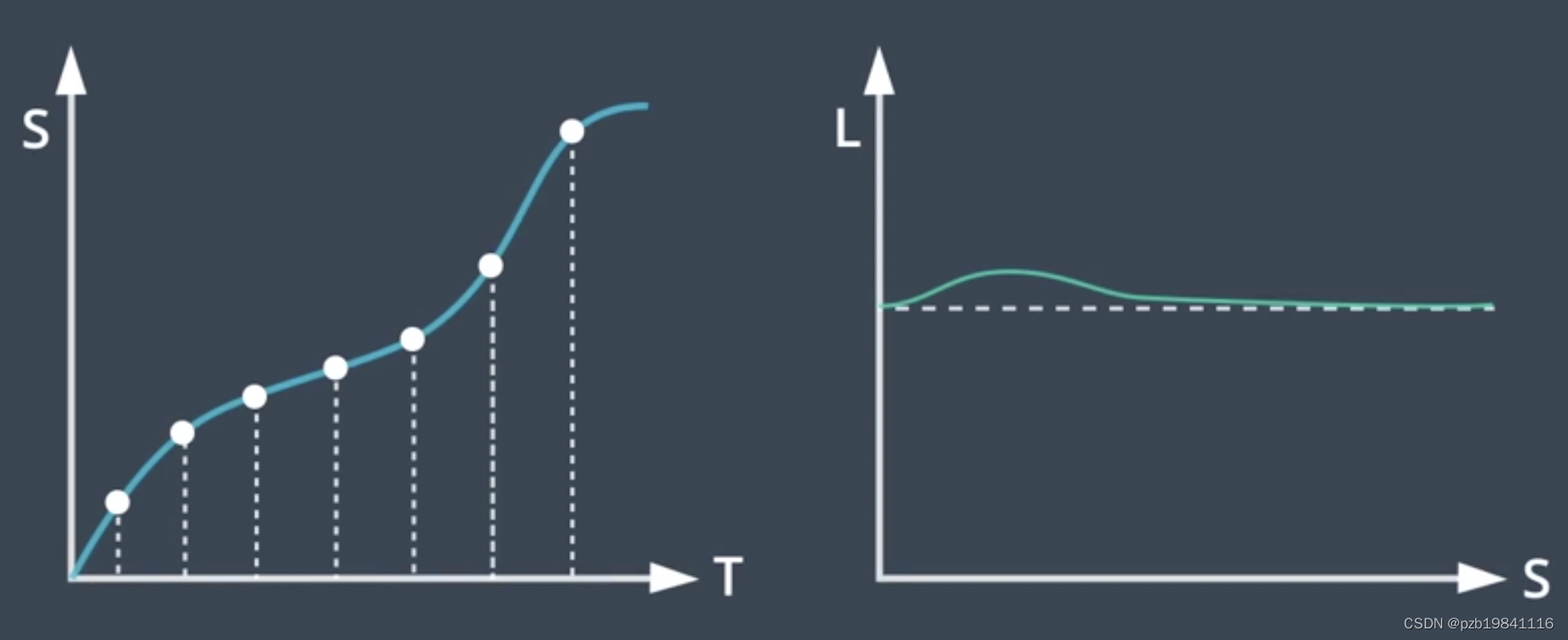
生成XYTime一个三维估计,两个坐标系中都有S,找同一个S,对应的L和T。
Apollo如何求解规划问题
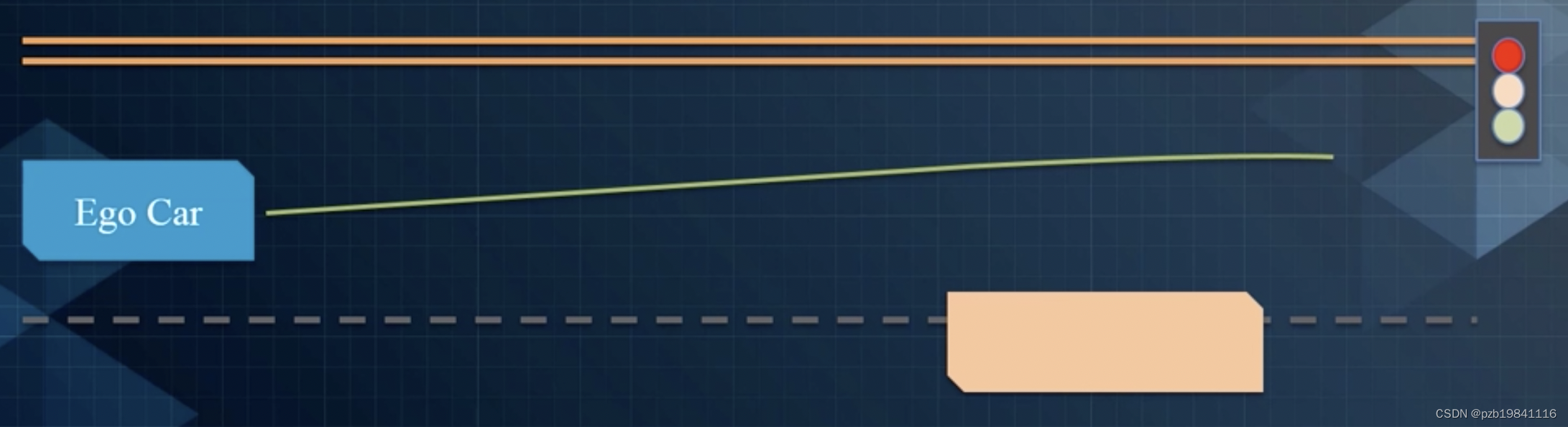
常用的方法叫Apollo EM Planner,用的期望值最大化的方法。
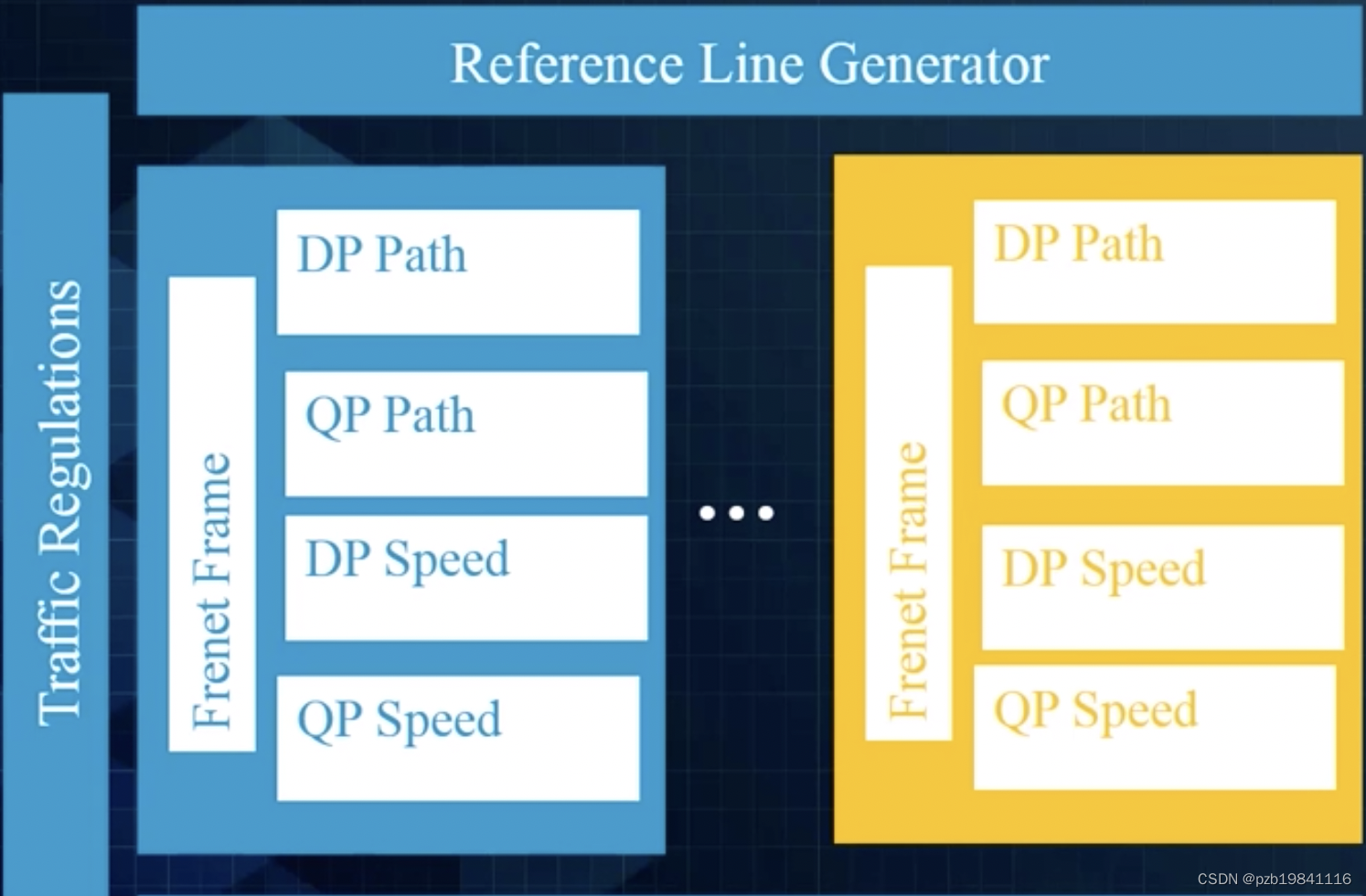
先生成一条Optimal P阿糊涂,再生成一条当前Path情况下的Optimal Speed。再将目前的Speed返回去给Path进行一次Tuning,将Tuning的Path返回来给Speed做优化,最后迭代到最优解。
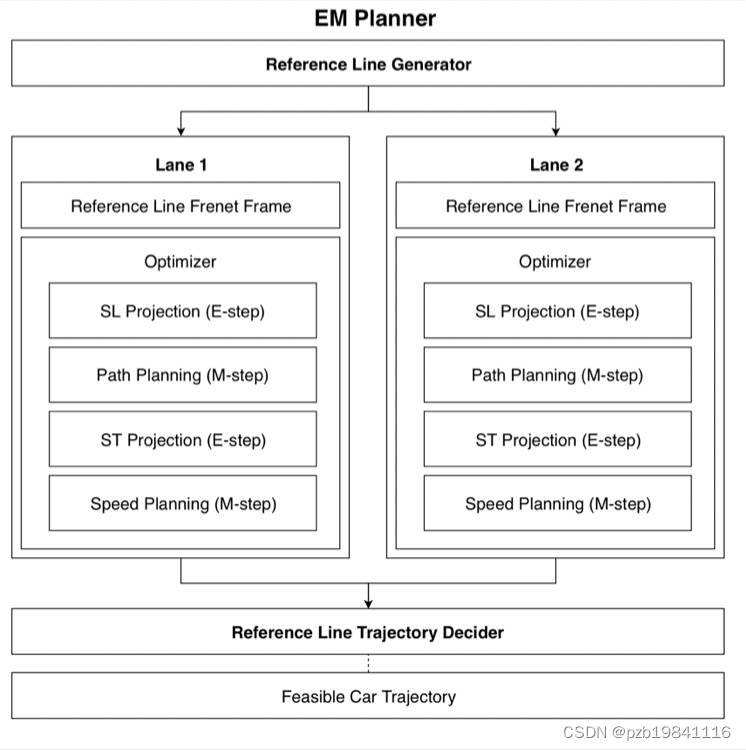
三个关键步骤:
目标函数:线性加权的Cost限制条件:交通规则,碰撞条件,动态特征优化求解:如何计算最优解(DP+QP)
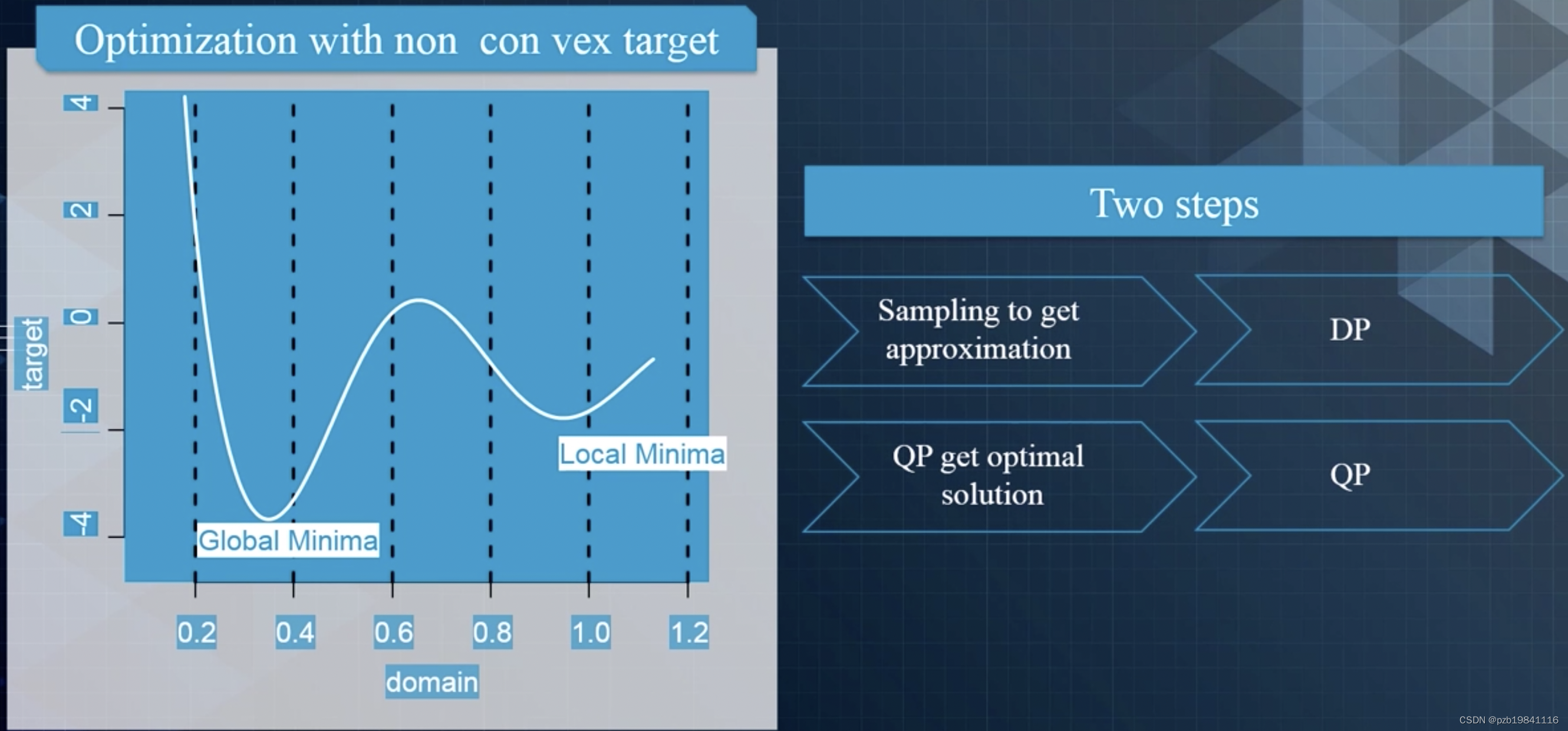
DP:不要求问题是凸的。QP:是一种凸优化。
Path QP
问题抽象:根据当前驾驶信息和道路情况建立平滑的SL坐标轨迹模型建立:合理优化目标函数和约束条件优化方法:二次优化求解带约束的二次规划问题

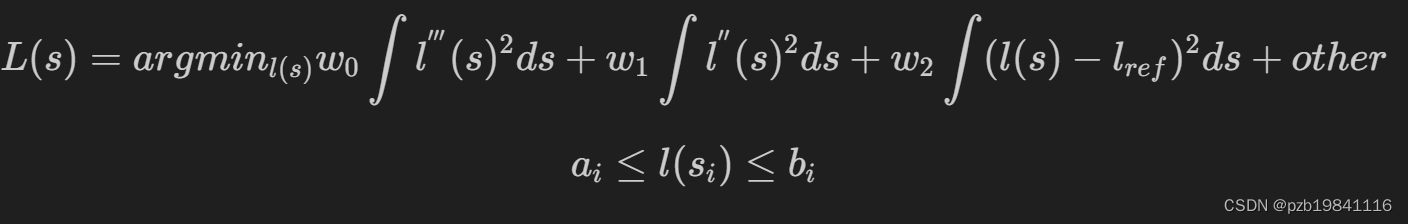
Speed DP
问题抽象:使用ST图模型建立:Cost函数优化方法:DP最有求解

计算提速思路:
SL坐标系离散化处理:什么时候用粗分辨率什么时候用细分辨率;GPU并行计算:同时计算多条Reference Lane的结果QP Hotstart:QP的性质,两帧之间差距不大。